目录
1.线性规划几何分析(Linear programming geometry)
2.线性规划代数分析(Linear programming algebraic)
4.线性规划矩阵分析(Linear programming matrix)
1.线性规划几何分析(Linear programming geometry)
1.1 LP模型
标准的线性规划模型如左图:n个变量,m个约束,最小化,约束不等,变量非负。
不标准的LP模型需要转换成标准LP
- 想要最大化:加负号变成最小化
- 有一个变量x取负值:用 x(+) - x(-) 代替 x,其中x(+)和x(-)均非负
- 有一个等式约束:分解成两个不等式约束
- 变量取整数:该模型属于MIP问题,不属于LP
- 有非线性约束:线性规划中的约束都是线性的

1.2 LP几何性质
- 凸集(Convex sets):对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内
- 凸组合(Convex combinations):若干个点的某种特定意义下的非负线性组合
- 凸集与凸组合关系:如果对于某空间中的集合S,其中任何点的凸组合也包括在S中,那S一定是凸集
- 凸集的交集也是凸集
- 一半的空间也是凸集,比如一个线性不等式会将空间分成两半,两半都是凸集
- 一些一半空间的交集也是凸集,被称为多面体(polyhedron),有限的多面体称为多胞形(polytope)

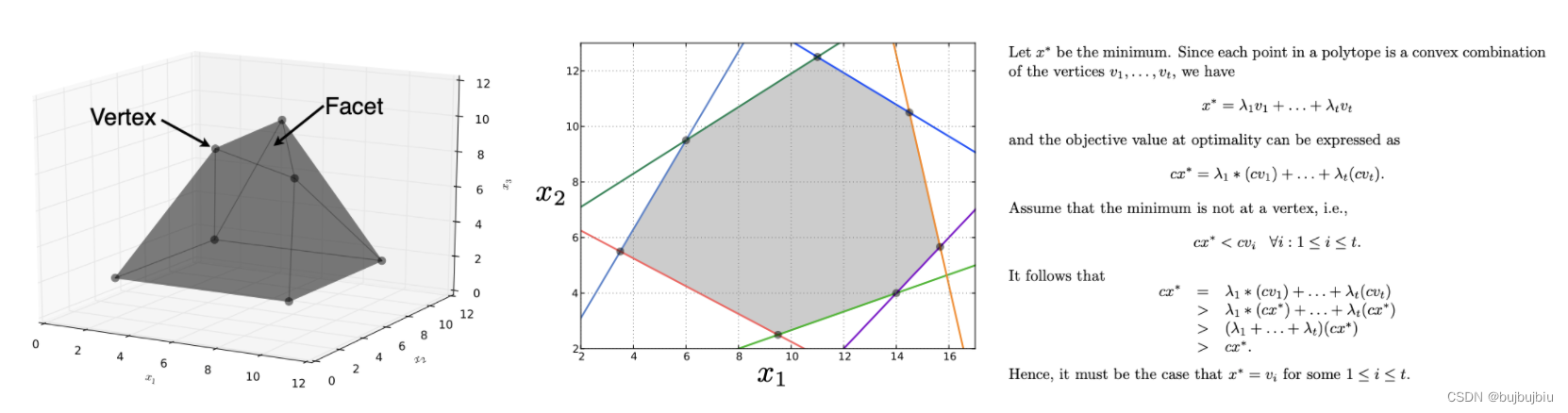
- 线性规划问题解空间为凸集,根据凸集性质可推出:线性规划模型如果有最优解,最优解一定出现在顶点
2.线性规划代数分析(Linear programming algebraic)
根据几何性质,可以得到求解LP问题的思路:迭代所有的顶点,选择最小目标值的点即为最优解。单纯形法(simplex algorithm)用更高效的方式探索这些顶点,由G. Dantzig发明,其思路可以理解为五步:
- 最优解位于顶点
- 每个顶点都是一个基础可行解BFS
- 可以从一个BFS移到另一个BFS
- 可以判断一个BFS是否最优
- 从任何BFS出发,都能找到方法得到更优的BFS
(1)找到基础可行解:选择m个变量作为基础变量(basic variables),其余变量为非基础变量(non basic variables),用非基础变量表达基础变量,如右图所示,如果b全部非负,则找到了一个可行解,非基础变量取值0,基础变量取值b(i)。
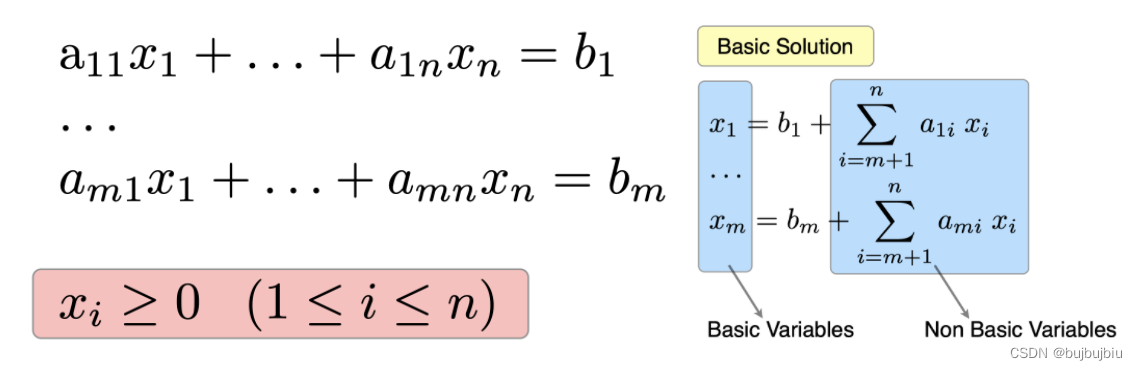
如果约束为不等式,增加松弛变量

找到基础可行解就可以得到这样一个求解思路:通过上述方法生成所有的基础可行解,然后选择最优的一个。但是对于大规模问题,基础解随变量和约束数量指数增加,完全遍历不可行
3.单纯形法(simplex algorithm)
前面提到完全遍历所有可行解不可行,需要更高效的搜索方法,采用局部搜索,由于线性规划解空间是凸集,因此一定能找到全局最优。
(2)从基础可行解移动到另一个基础可行解:使用局部搜索的思路,交换一个基础变量和非基础变量
- entering variable:选择一个在右边等式里系数均为负的非基础变量作为换入变量,然后变成基础变量
- leaving variable:选择一个基础变量换出变成非基础变量,某些基础变量换出后解可能不可行,因此不能随机选择leaving variable,为了保存可行性,选择常数值和换入变量系数负比值最小的行的基础变量作为换出变量,在执行完高斯消除后能保证右侧b>0

(3)判断一个基础可行解是否为最优:找到一个BFS后,消除目标函数里的所有基础变量,如果消除后的函数里非基础变量的系数非负,则已经找到最优解

(4)每次从BFS移动到另一个BFS都是改进:局部移动假设了右侧的b值永远是正的,并且目标函数有下届,因此按照单纯形法迭代一定能最终找到最优解结束。但是有以下特殊情况
- 没有换出变量,表明可能目标函数值无解。如下x1无法被换出,表明目标函数不能消除x1,不能实现非基础变量的系数非负,没有最优解,即无边界解
- 有些b为0,无论怎么交换,换出变量都会是其对应行
针对这些会造成单纯形法迭代无法终止的情况,可以设置一些换入换出原则,如总是选择第一个变量换出,增加扰动等

4.线性规划矩阵分析(Linear programming matrix)
一个线性规划模型包含两类变量:基础变量和非基础变量,其对应系数矩阵分为基础矩阵和非基础矩阵
,因此模型可以用矩阵表示为
,经过转化可得基础可行解
,目标函数值同样可以用基础变量和非基础变量表示
,代入
公式转换得到
,其中
。根据前面的结论,如果
非负,则
为最优解。

单纯形法迭代通常以表格的形式,简单直观,如下图,基础变量为x3,x4,x5,换入变量选择x2,根据换出原则选择x3
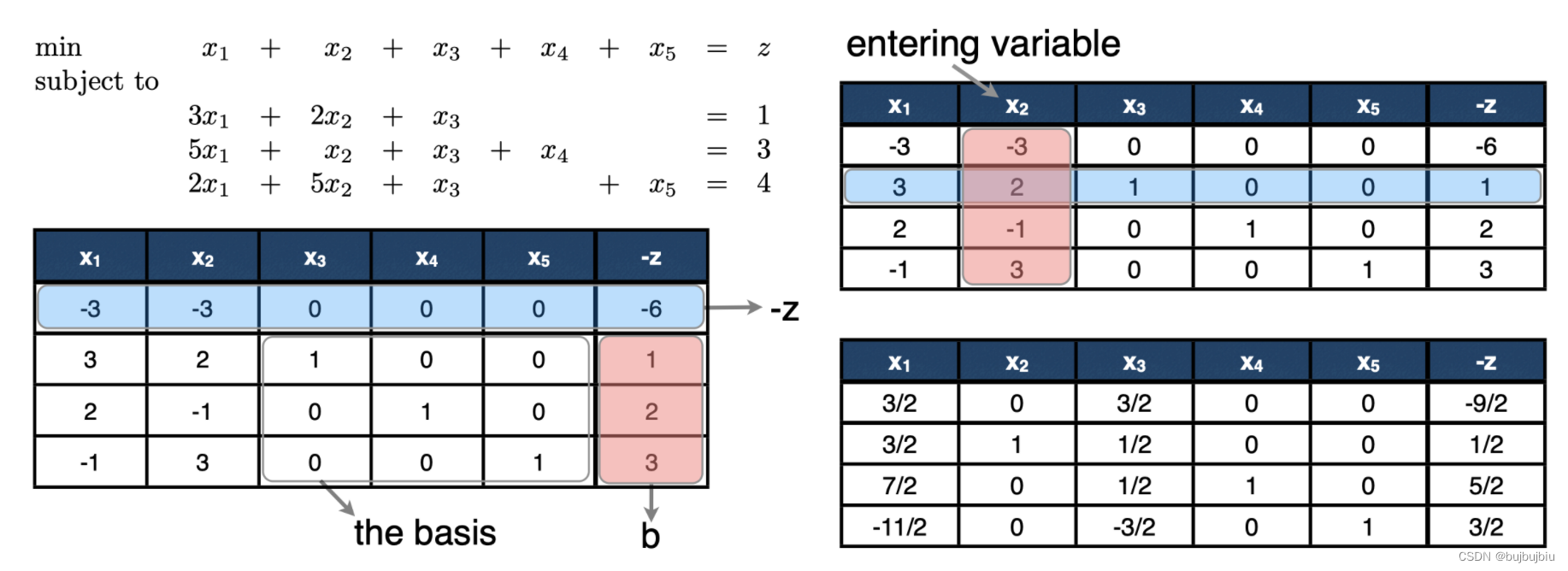
5.对偶模型(Duality)
给定一个线性规划模型,可以通过一些规则得到其对偶模型,Prima模型的约束条件对应Dual模型的变量,Prima的b值变成Dual目标函数的系数,Prima的约束条件系数转置变成Dual约束条件系数,Dual约束符号和变量符号取决于原先变量和约束的符号,见下右图对应。
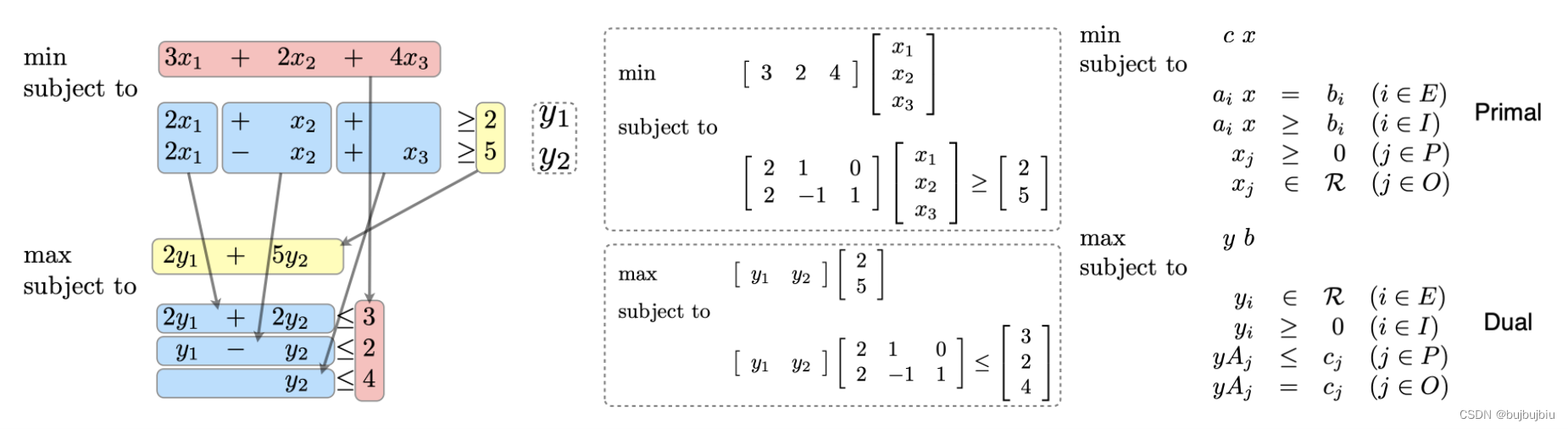
对偶理论:如果原始模型有最优解,那么对偶模型也有使目标函数取值相同的最优解
原始模型(最小化)的目标函数值一定大于对偶模型(最大化)的目标函数值,原始模型向着目标值变小的方向,对偶模型向着目标值变大的方向,最终两者目标值相同,都找到最优解。

对偶的对偶是原始,如果原始模型无可行解,那么对偶模型无可行解或者无界解
对偶模型提供了一种证明当前解最优的思路, 给定原始模型解x,对偶模型解y,如果两者的目标函数值相同,那么x,y分别是最优解

互补松弛定理(Complementarity Slackness):如果和
分别是原始和对偶问题的可行解,如果代入值后原始模型某个约束条件不等,那么对应的对偶变量一定为0,如果某个原始变量取值不为0,那么对应的对偶约束取等号。

使用对偶模型的好处在于:假设我有一个最优解,现在要添加一个新约束,添加约束后原始模型不可行,但是对偶模型可行,因此可以优化对偶模型找到最优解。原始模型和对偶模型的单纯形法迭代可以使用同一个表格
