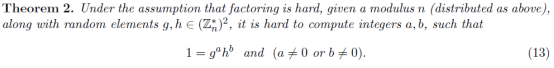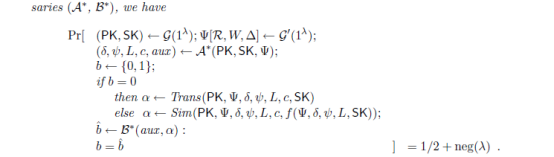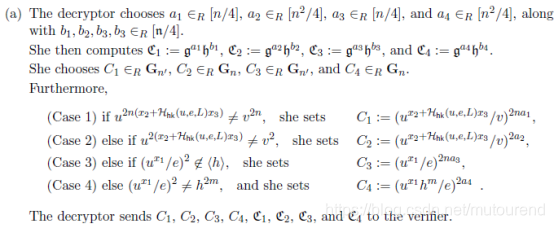Practical Verifiable Encryption and Decryption of Discrete Logarithms 学习笔记

1 引言

Jan Camenisch 和 Victor Shoup 2003年论文《Practical Verifiable Encryption and Decryption of Discrete Logarithms》。

对应的代码实现在：https://github.com/KZen-networks/dlog-verifiable-enc

经验证，node版本用V10.20.1可以，用12版本存在兼容问题。
该代码用到了neon框架：Rust bindings for writing safe and fast native Node.js modules. 即内部是rust程序，外部是nodejs。

在该论文中主要关注的是proving properties about encrypted data.
在public-key encryption场景下，主要存在两方：

• 生成密文的一方；
• 拥有私有的一方。

协议也可分为：

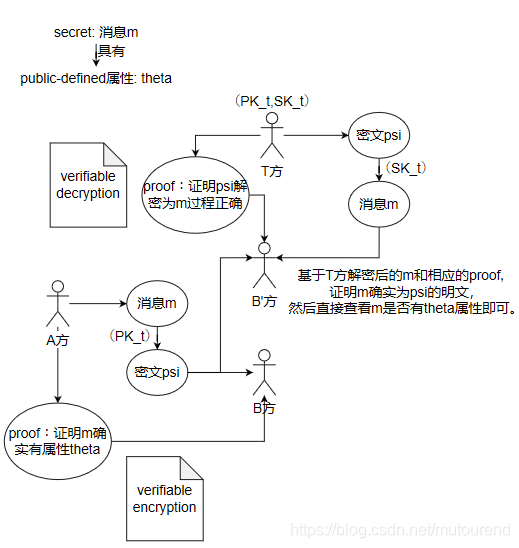
• 若由加密方来提供证明，则称为verifiable encryption protocol；（本文主要关注verifiable encryption of discrete logarithm）
• 若由解密方来提供证明，则称为verifiable decryption protocol。（本文主要关注verifiable decryption of discrete logarithm）

具体描述如下图所示：

本论文只关注discrete logarithm属性：

• $\psi=Enc_{pk}(m)$，且 $m$具有 $\delta=\gamma^m$属性，其中 $\psi,PK,\delta,\gamma$ 对A方和B方均已知（为common input）；
• $\psi=Enc_{pk}(m_1,m_2,\cdots,m_k)$，且 $(m_1,m_2,\cdots,m_k)$具有 $\delta=\gamma_1^{m_1}\gamma_2^{m_2}\cdots\gamma_k^{m_k}$属性，其中 $\psi,PK,\delta,(\gamma_1,\gamma_2,\cdots,\gamma_k)$ 对A方和B方均已知（为common input）。

以上两类discrete logarithm属性在 key escrow秘钥托管，optimistic fair exchange乐观公平交互，publicly verifiable secret and signature sharing可公开验证的密码和签名共享，universally composable commitments通用组合承诺，group signatures群签名，和confirmer signatures确认人签名 等密码学应用场景中均非常有用。

• 本文的encryption scheme在Cramer and Shoup public key encryption scheme的基础上做了改进，可抵抗chosen ciphertext attack选择密文攻击；
• 本文的proof protocol，采用的是常用的three move “ $\Sigma$-protocol”。
• 本文的decryption过程除了verifiable decryption protocol外，也可以用threshold decryption protocol来实现，这样可以减少对decryptor的信任依赖。

1.1 verifiable encryption protocol

本文的verifiable encryption protocol 主要基于以下关键技术：

• Fujisaki and Okamoto’s method for proving relations on committed values [FO97] (with some refinements, as in [CS00, DF02])；
• the related interval proofs [CM98, CFT98]；
• Paillier encryption [Pai99]；
• Cramer and Shoup’s universal hash proof encryption technique [CS02]。

1.2 verifiable decryption protocol

本文的verifiable decryption protocol主要基于以下关键技术：

• Cramer, Damg˚ard, and Schoenmakers’ proofs of partial knowledge [CDS94]；
• Boudot’s exact interval proofs [Bou00]；
• new protocols for proving the inequality of discrete logarithms。

1.3 一些定义

$a,b,c$为整数，且 $b>0$。

• non-negative remainder
  $c=a\mod b$，其中 $c=a-\left \lfloor a/b \right \rfloor b$，所以有 $0\leq c<b$。

• balanced remainder
  $c=a\ rem\ b$，其中 $c=a-\left \lfloor a/b \right \rceil b$，所以有 $-b/2 \leq c<b/2$。若 $b$为奇数，则对所有的 $a$均满足 $-(b-1)/2 \leq a\ rem\ b \leq (b-1)/2$。

• ordinary honest-verifier zero-knowledge protocol
  是指若Prover在生成commitment $t$之前，已经预知了challenge $c$的值，则Prover在不知道witness $x$的情况下，可伪造任意的 $(t,s)$，使得Verifier验证均可通过。（可参见博客 基于Sigma protocol实现的零知识证明protocol集锦 第1.2.2节内容。）

• 支持附加label的secure public-key encryption
  A label is an arbitrary bit string that is input to the encryption and decryption algorithms, specifying the “context” in which the encryption or decryption operation is to take place.

public key encryption scheme中主要包含三类算法：
– probabilistic, polynomial-time key generation算法：输入为 $1^{\lambda}$，其中 $\lambda \geq 0$为security parameter，输出公私钥对 $(PK,SK)$，其中公钥 $PK$ 明确规定了a finite, easy-to-recognize message space $M_{PK}$。
– probabilistic, polynomial-time encryption算法：输入为公钥 $PK$、消息 $m\in M_{PK}$、label $L$，输出为密文 $\psi$。
– deterministic, polynomial-time decryption算法：输入为私钥 $SK$、密文 $\psi$、label $L$，输出为消息 $m\in M_{PK}$（其中 $PK$为 $SK$对应的公钥），或者为特别的reject标识。

2. Encryption Scheme

假设 $p,q,p’,q’$均为不同的odd primes，满足 $p=2p’+1,q=2q’+1$，其中 $p’,q’$的长度均为 $l$。素数 $p’,q’$被称为Sophie Germain primes，素数 $p,q$被称为safe primes。
目前无证据证明存在无穷多的Sophie Germain primes，有经验证明 a random $l$-bit number is Sophie Germain prime的概率为 $\Omega(1/{l^2})$。

设置 $n=pq,n’=p’q’$。
Group： $\mathbb{Z}_{n^2}^*$
Subgroup of $\mathbb{Z}_{n^2}^*$： $\mathbf{P}$，包含了all $n$-th powers of elements in $\mathbb{Z}_{n^2}^*$。
即 $x\in \mathbb{Z}_{n^2}^*$， $y=x^n\mod n^2$， $y\in \mathbf{P}$

根据Paillier’s Decision Composite Residuosity (DCR)假设：
若仅知 $n$的情况下，it is hard to distinguish random elements of $\mathbb{Z}_{n^2}^*$ from random elements of $\mathbf{P}$。

Paillier’s DCR假设中未对safe primes $p,q$ 做约束，为了描述更清楚，本论文中添加了约束。

将 $\mathbb{Z}_{n^2}^*$分解为 an internal direct product：
$\mathbb{Z}_{n^2}^*=\mathbf{G}_n\cdot \mathbf{G}_{n’}\cdot \mathbf{G}_2\cdot \mathbf{T}$
其中：

• $\mathbf{G}_n$为a cyclic group of oreder $n$。唯一的。
• $\mathbf{G}_{n’}$为a cyclic group of oreder $n’$。唯一的。
• $\mathbf{T}$为subgroup of $\mathbb{Z}_{n^2}^*$ generated by $-1 \mod n^2$。唯一的。
• $\mathbf{G}_2$ 存在2种可能的选择。
• 对于任意的 $x\in \mathbb{Z}_{n^2}^*$，可将其唯一的表示为 $x=x(\mathbf{G}_n)x(\mathbf{G}_{n’})x(\mathbf{G}_2)x(\mathbf{T})$，其中 $x(\mathbf{G}_n)\in \mathbf{G}_n, x(\mathbf{G}_{n’})\in \mathbf{G}_{n’}, x(\mathbf{T})\in \mathbf{T}$。
• 注意element $h=(1+n\mod n^2)\in \mathbb{Z}_{n^2}^*$具有order $n$，同理对于 $0\leq a<n$有 $h^a=(1+an\mod n^2)$ 具有的order也为 $n$。

对应地，subgroup $\mathbf{P}$可分解为：
$\mathbf{P}=\mathbf{G}_{n’}\cdot \mathbf{G}_2\cdot \mathbf{T}$

定义map $abs: \mathbb{Z}_{n^2}^* \rightarrow \mathbb{Z}_{n^2}^*$：【即相当于balanced remainder】【引入 $abs(\cdot)$来保证non-malleability。】

• 当 $n^2/2<a<n^2$时，对应为将 $a\mod n^2$ map to $(n^2-a\mod n^2)$；
• 否则当 $0<a\leq n^2/2$时，对应为将 $a\mod n^2$ map to $a\mod n^2$。

对应地有：

• 对于任意的 $v\in \mathbb{Z}_{n^2}^*$， $v^2=(abs(v))^2$ 恒成立。

2.1 Key Generation

Key Generation 基本流程为：

• 随机选择两个 $l$-bit Sophie Germain primes $p’,q’$， $p’\neq q’$。
• 计算： $p=2p’+1,q=2q’+1,n=pq,n’=p’q’$，其中 $l=l(\lambda)$为辅助security parameter。
• 选择随机数 $x_1,x_2,x_3\in_R [n^2/4]$，选择随机数 $g’\in_R \mathbb{Z}_{n^2}^*$。
• 计算： $g=(g’)^{2n}, y_1=g^{x_1},y_2=g^{x_2},y_3=g^{x_3}$。
• 生成hash key $hk$ from the key space of the hash scheme $H$ associated with the security parameter $\lambda$。

对应的公钥为 $(hk, n, g, y_1,y_2,y_3)$，私钥为 $(hk,n,x_1,x_2,x_3)$。

设置 $h=(1+n\mod n^2)\in \mathbb{Z}_{n^2}^*$， $h$为an element of order $n$。

2.2 Encryption

使用公钥 $(hk, n, g, y_1,y_2,y_3)$对消息 $m\in [n]$ with label $L\in {0,1}^*$进行加密，加密流程为：

• 选择随机数 $r\in_R[n/4]$。
• 计算： $u=g^r,e=y_1^rh^m,v=abs((y_2y_3^{H_{hk}(u,e,L)})^r)$

生成的密文信息为 $(u,e,v)$。

2.3 Decryption

使用私钥 $(hk,n,x_1,x_2,x_3)$对密文 $(u,e,v)\in \mathbb{Z}_{n^2}^*\times \mathbb{Z}_{n^2}^*\times \mathbb{Z}_{n^2}^*$ with label $L$ 进行解密，解密流程为：

• 验证 $abs(v)=v$是否成立，以及 $u^{2(x_2+H_{hk}(u,e,L)x_3)}=v^2$是否成立，若不成立直接返回reject，不做后续处理。
• 设置 $t=2^{-1}\mod n$。
• 计算： $\hat{m}=(e/u^{x_1})^{2t}$。
• 若 $\hat{m}$ is of the form $h^m$ for some $m\in [n]$，则输出 $m$；否则输出reject。

注意，若将 $abs(\cdot)$替换为identity function，那么整个encryption scheme具有延展性malleable， $(u,e,v)$和 $(u,e,-v)$均为消息 $m$ with label $L$的密文。

若DCR assumption成立且 $H$为collision resistant，则以上encryption scheme可抵抗adaptive chosen ciphertext attack。

2.4 扩展至Threshold Decryption

由于在decryption时不需要知道the knowledge of the factorization of $n$，所以2.3节的decryption可很容易转换为threshold decryption。可参考[SG98]或[CG99]的思路来实现。

3. Strong RAS Assumption and Factoring Assumption

Strong RSA Assumption：（可参看博文 密码学中的各种假设——DL/SDH…）

4. Verifiable Encryption

• $(\mathcal{G},\varepsilon, \mathcal{D})$表示a public key encryption scheme。
• $(PK,SK)$表示公私钥对。

所谓verifiable encryption scheme：
Proves that a ciphertext encrypts a plaintext satisfying a certain relation $\mathcal{R}$。
证明某密文所加密的信息满足特定的relation $\mathcal{R}$。

4.1 Verifiable Encryption Scheme定义

【其实就是证明2.2节的Encryption算法执行正确。】
verifiable encryption scheme中：

• 加密方：输入有 $\delta$，满足 $\delta=\gamma^{w}$的 $w$，以及label $L$，基于 $L$和 $w$加密生成密文 $\psi$。（encrypts $w$ under $L$, yielding a ciphertext $\psi$）
  加密算法为 $\varepsilon(PK,m,L)=\psi$
• 加密方：生成proof，证明 $\psi$ decrypts under $L$ to a witness for $\delta$。需要用到密文及生成密文所使用的随机数值 $coins$（参见第2.2节Encryption中的随机数 $r$）。
  $\varepsilon'(PK,m,L)=(\psi,coins)$。
  instead of requiring $\psi$ decrypts under $L$ to a witness，改为要求存在有效的reconstruction算法， $recon(PK,\Psi,\delta,m)=w$，其中 $m\in M_{PK} \cup \{reject\}$， $w\in W\cup \{reject\}$。对于所有的 $(w,\delta)\in\mathcal{R}$， $recon(PK,\Psi,\delta,w)=w$均成立。

verifiable encryption scheme详细定义如下图所示，其中：

• $\mathcal{G}$为public key encryption scheme的generator算法，用于生成公私钥对 $(PK,SK)$。（参见第2.1节中的Key Generation算法）
• $\varepsilon$为public key encryption scheme的加密算法，用于生成密文。
• $\mathcal{G}’$为 relation $\mathcal{R}$的generator算法，输入为 $1^{\lambda}$，输出为a description $\Psi=\Psi[\mathcal{R},W,\Delta]$ of a binary relation on $\mathcal{R}$ on $W\times \Delta$。
  
  本文主要关注的relation $\mathcal{R}$ 为discrete logarithm 属性。
  如 $\delta=\gamma^{w}$，表示为 $\delta\in\Delta,w\in W$， $(w,\delta)\in \mathcal{R}$，被称为a witness $w$ for $\delta$。

4.2 Verifiable Encryption of a Discrete Logarithm

以2.1节的公钥 $(hk,n,g,y_1,y_2,y_3)$为例，相应的message space associated with this public key is $[n]$。

设置 $\Gamma$为a cyclic group of order $\rho$ generated by $\gamma$，假设 $\gamma,\rho$为publicly known，且 $\rho$为prime。
设置 $W=[\rho],\Delta=\Gamma$， $\mathcal{R}=\{(w,\delta)\in W\times \Delta:\gamma^w=\delta\}$。本节主要关注的内容是“discrete logarithm” relation $\mathcal{R}$。

要求 $n>\rho$、 $2^k<min\{p’,q’,\mathfrak{p’},\mathfrak{q’},\rho\}$且 $\rho<n2^{-k-k’-3}$。其中 $k=k(\lambda),k’=k’(\lambda)$为further security parameters， $2^{-k(\lambda)}和2^{-k’(\lambda)}$为negligible functions， $\{0,1\}^k$为Verifier的challenge space， $k’$ controls the quality of the zero-knowledge property。使得 $\log_{\gamma}\delta$ “fits into an encryption”。（If this condition is not meet, the value $\log_{\gamma}\delta$ could be split into smaller pieces, each of which would then be verifiably encrypted.）

Verifiable Encryption of a Discrete Logarithm 生成proof时需用到的augmented public key信息：

• Setup：需引入辅助信息 $\mathfrak{n}$，为 $\mathfrak{l}+1$-bit safe primes $\mathfrak{p}=2\mathfrak{p’}+1$和 $\mathfrak{q}=2\mathfrak{q’}+1$的乘积，即 $\mathfrak{n}= \mathfrak{p} \mathfrak{q}, \mathfrak{n‘}= \mathfrak{p’} \mathfrak{q‘}$。
  $\mathfrak{g}, \mathfrak{h}$为 $\mathfrak{G}_{\mathfrak{n’}}\subset \mathbb{Z}_{\mathfrak{n}}^*$的两个generators。 $\mathfrak{G}_{\mathfrak{n’}}$为subgroup of $\mathbb{Z}_{\mathfrak{n}}^*$ of order $\mathfrak{n’}$， $\mathfrak{l}=\mathfrak{l}(\lambda)$。

以上辅助信息用于生成proof使用，注意 $\mathfrak{n}$的因式分解应对prover未知。整个setup由可信第三方来构建。（该辅助信息可与Encryption scheme中共用相同的 $\mathfrak{n}=n$。）

对Prover和Verifier的common input有：

• public key $(hk,n,g,y_1,y_2,y_3)$
• augmented public key $(\mathfrak{n},\mathfrak{g},\mathfrak{h})$
• group element $\delta$
• ciphertext $(u,e,v)$
• label $L$

Prover additional input有：

• 消息m，使得 $\delta=\gamma^m$成立。
• 加密过程中用到的随机数 $r\in_R[n/4]$，使得 $u=g^r,e=y_1^rh^m,v=abs((y_2y_3^{H_{hk}(u,e,L)})^r)$成立。

Verifiable Encryption of a Discrete Logarithm生成proof流程为：

• Prover：选择随机数 $s\in_R [\mathfrak{n}/4]$，计算 $\mathfrak{k}=\mathfrak{g}^m\mathfrak{h}^s$。将 $\mathfrak{k}$发送给Verifier。
• Prover：选择随机数 $r’\in_R [-n2^{k+k’-2},n2^{k+k’-2}], s’\in_R [-\mathfrak{n}2^{k+k’-2},\mathfrak{n}2^{k+k’-2}],m’\in_R [-\rho2^{k+k’},\rho2^{k+k’}]$，计算 $u’=g^{2r’},e’=y_1^{2r’}h^{2m’},v’=(y_2y_3^{H_{hk}(u,e,L)})^{2r’},\delta’=\gamma^{m’},\mathfrak{k’}=\mathfrak{g}^{m’}\mathfrak{h}^{s’}$。将 $u’,e’,v’,\delta’, \mathfrak{k’}$发送给Verifier。
• Verifier：选择随机challenge $c\in_R \{0,1\}^k$，将 $c$发送给Prover。
• Prover：计算response $\tilde{r}=r’-cr, \tilde{s}=s’-cs, \tilde{m}=m’-cm$ (computed in $\mathbb{Z}$)，将 $\tilde{r},\tilde{s},\tilde{m}$发送给Verifier。
• Verifier：验证 $u’=u^{2c}g^{2\tilde{r}},e’=e^{2c}y_1^{2\tilde{r}}h^{2\tilde{m}},v’=v^{2c}(y_2y_3^{H_{hk}(u,e,L)})^{2\tilde{r}},\delta’=\delta^c\gamma^{\tilde{m}},\mathfrak{k’}=\mathfrak{k}^c\mathfrak{g}^{\tilde{m}}\mathfrak{h}^{\tilde{s}},-n/4<\tilde{m}<n/4$所有公式均成立。
• Verifier：验证 $v=abs(v)$成立。

4.3 Verifiable Encryption of $l$ Discrete Logarithms

在4.2节对1个消息的encryption Discrete Logarithm属性的基础上，扩展至 $l$个消息。
实现方式是用多个 $y_1$来生成多个 $e$。
在2.1节的基础上，secret key变为 $(hk, x_1^{(1)},\cdots,x_1^{(l)},x_2,x_3)$，其中 $x_1^{(1)},\cdots,x_1^{(l)},x_2,x_3\in_R [n^2/4]$，public key变为 $(hk,n,g,y_1^{(1)},\cdots,y_1^{(l)},y_2,y_3)$，其中 $y_1^{(i)}=g^{x_1^{(i)}}$。

encrypt消息 $m^{(i)}\in [n]$ with label $L\in \{0,1\}^*$ under the public key as above，选择随机数 $r\in_R [n/4]$，计算：
$u=g^r,e^{(i)}=(y_1^{(i)})^rh^{m^{(i)}},v=abs((y_2y_3^{H_{hk}(u,e,L)})^r)$

对应的，decrypt流程类似如2.3节所示。

5. Prove inequality of discrete logarithms

可参加博客 基于Sigma protocol实现的零知识证明protocol集锦 第2.7节内容。

6. Verifiable Decryption

【其实就是证明2.3节的Decrypt算法执行正确。】
Verifiable Decryption proof其实是由第1节所画图中的T方执行生成的。

本论文中提到的PK protocol指的是博客 基于Sigma protocol实现的零知识证明protocol集锦 第2.5节内容 “Equality of the opening of 2 Pedersen commitment “。

待证明：
$u^{2(x_2+H_{hk}(u,e,L)x_3)}/{v^2}=1$ 且 $(e/{u^{x_1}})^2/{h^{2m}}=1$

以上为AND证明，对应该证明不成立存在以下四种情况：

Prover（ $T$方，即decryptor）和Verifier（ $B‘$方）的Common input有：

• public key $(hk,n,g,y_1,y_2,y_3)$
• augmented public key $(\mathfrak{n},\mathfrak{g},\mathfrak{h})$
• ciphertext $(u,e,v)$
• message $m$
• label $L$

Prover（ $T$方，即decryptor）的additional input为：

• 私钥 $(x_1,x_2,x_3)$

Verifiable Decryption基本流程为：

• 1）Prover：判断 $m,( u, e,v)$是否合法，若 $m\notin [n]$或者 $v\neq abs(v)$，则返回-1，不执行后续步骤。

• 2）Prover：若 $( u, e,v)$为有效密文，且确实在Label $L$的基础上解密为 $m$，则输出1给Verifier。同时，生成AND proof，证明Prover确实知道相应的私钥 $(x_1,x_2,x_3)$使得如下协议成立。
  $PK\{(x_1,x_2,x_3):y_1=g^{x_1} \wedge y_2=g^{x_2} \wedge y_3=g^{x_3} \wedge v^2=u^{2x_2}u^{2H_{hk}(u,e,L)x_3} \wedge \frac{e^2}{h^{2m}}=u^{2x_1}\}$

• 3）Prover：若 $(u,e,v)$在Label $L$下为无效密文或者解密结果不同于 $m$，则输出-1给Verifier。同时，要生成OR proof，证明Prover的判断解密是正确的。（OR证明思路可参见博客 基于Sigma protocol实现的零知识证明protocol集锦 第2.3节内容 和 博客 Proof Systems for General Statements about Discrete Logarithms 学习笔记 第3节内容。）

7. Verifiable Decryption of a Discrete Logarithm

【注意，此时消息 $m$并不直接发送给Verifier。】

在第6节的基础上，额外增加的内容是：要求所解密的消息 $m$满足 $\delta=\gamma^{m}$。
即需要满足的方程式有：
$ u^{{2(x_2+H_{hk}(u,e,L)x_3)}/{v}2}=1$ 且 $(e/{u^{x_1}})^2/{h^{2m}}=1$ 且 $\delta=\gamma^{m}$

由于 $h=(1+n\mod n^2)\in\mathbb{Z}_{n^2}^*$具有的order为 $n$，于是有 $h^n\mod n^2=1$，相应的由 $(e/{u^{x_1}})^2/{h^{2m}}=1$可推导出 $(e/{u^{x_1}})^{2n}=1\mod n^2$。
同时 $\delta=\gamma^{m}$即对应要求 $(m\ rem\ n)\equiv \log_{\gamma}\delta(\mod \rho)$。

于是待证明的内容演变为：
$ u^{{2(x_2+H_{hk}(u,e,L)x_3)}/{v}2}=1$ 且 $(e/{u^{x_1}})^{2n}=1$ 且 $\delta=\gamma^{(\log_{h^2}(e/u^{x_1})^2\ rem\ n)}$

前两个等式成立的证明可采用第6节类似的方式。

$\delta=\gamma^{(\log_{h^2}(e/u^{x_1})^2\ rem\ n)}$的证明可拆分为：

• 1）证明 $m=\log_{h^2}(e/u^{x_1})^2\ rem\ n$成立。
• 2）证明 $m=log_{\gamma}\delta\mod \rho$成立。
• 3）证明 $m\in[-(n-1)/2,(n-1)/2]$。

其中1）和2）可利用之前augmented public key $(\mathfrak{n},\mathfrak{g},\mathfrak{h})$采用第6节类似的方式来证明，under the strong RSA assumption。

证明 $m\in[-(n-1)/2,(n-1)/2]$。与4.2节验证 $-n/4<\tilde{m}<n/4$内容不同。此处要求the interval proof be exact。
由于 $m\in[-(n-1)/2,(n-1)/2]$为对称区间，可进一步转换为证明 $((n-1)/2)^2-m^2\geq 0$。【注意后续证明流程中的 $w_1,w_2,w_3,w_4$的取值。】

Prover（ $T$方，即decryptor）和Verifier（ $B‘$方）的Common input有：

• public key $(hk,n,g,y_1,y_2,y_3)$
• augmented public key $(\mathfrak{n},\mathfrak{g},\mathfrak{h})$
• ciphertext $(u,e,v)$
• group element $\delta$
• label $L$

Prover（ $T$方，即decryptor）的additional input为：

• 私钥 $(x_1,x_2,x_3)$

Verifiable Decryption of a Discrete Logarithm的基本流程如下所示：