基于粒子群和麻雀搜索的LMS自适应滤波算法

文章目录

基于粒子群和麻雀搜索的LMS自适应滤波算法

摘要：在自适应滤波算法中，LMS算法是最常用的算法之一，因为具备结构简单，易于实现，性能稳定，计算复杂度低等特
点。然而， LMS算法也存在缺点，比如，收敛速度较慢，收敛精度低的问题，这就影响LMS算法在收敛性要求较高的领域中的
应用。使用粒子群算法和麻雀搜索算法对 LMS算法进行改进，可以将 LMS滤波设计变成对 LMS滤波参数优化的问题，利用粒子群算法的优化能力，使得滤波参数得到全局最优解。以此可以提高 LMS滤波算法的收敛性能，从而提高滤波性能。

1.LMS 自适应滤波算法

LMS滤波器的基本结构，如图1所示。根据如图1所示，该图为LMS滤波器的基本原理框图：

在这里插入图片描述

图1.LMS滤波器基本结构

初始化时，如式（1）：
$w(0)=w(0)=[0 0 0 ... 0]^T$
当ｋ ≥０时，如式(２)、式(３)
$x^T(k)w(k) \tag{2}$

$=w(k)-2ue(k)x(k)\tag{3}$

其中，(k)为瞬时的误差，u为收敛因子，e(k)是误差信号，w(k)为的滤波器系数。按照梯度特性,w(k)在每次迭代运算中会自动调整，逐步是均值 $E[e^2(k)]$ 最小化， $E[e^2(k)]$ 就是最小均方差。

2.自适应滤波在降噪中的应用

当自适应滤波被应用在降噪应用中是，它的结构框图，如图 2 所示.

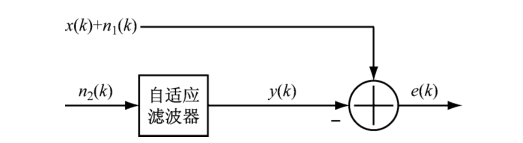
在这里插入图片描述

图2.信号降噪结构

与看见的自适应滤波器结构是不同的。信号 $x (k)$ 受到噪声 $n_1(k)$ 的影响。而信号 $n_2(k)$ 是与噪声相关的信号，它可以被测量到的信号。 $n_2(k)$ 也作为自适应滤波器的输入信号，受到干扰的信号 $x(k) + n_1(k)$ 作为期望信号。

输出信号 $y (k)$ 与输入信号 $n_2(k)$ 的数学关系式根据图１是式(4)
$\sum_{l=0}^{N}w_ln_2(k-l)\tag{4}$
按照均方误差方程，可以得到式(5)
$E[e^2(k)] = E[x^2(k)] + E{[n_1(k) - y(k)]^2}\tag{5}$
假如 $x (k)$ 与 $n_1(k)$ 和 $n_2(k)$ 无关，那么该函数的最小 $M S E$ 为式(6)
$\xi_{min} = E[e^2(k)] = E[x^2(k)]\tag{6}$
其中 $x (k)$ 就是我们滤波所要得到的信号。

3.粒子群算法对LMS滤波算法的改进

式２和式３所示的更新方程是LMS算法的最重要的工作步骤。根据梯度特性 $E[e^2(k)]$ 会不断趋于最小均方差。其中。从式2能够推倒出下式(7)。
$x^T(k+1)[w(k)-2ue(k)x(k)]\tag{7}$
$e (k)$ 是瞬时误差，根据式 7 所示，收敛因子2u决定了 $E[e^2(k)]$ 的最小值。许多研究都是针对2u ，通过动态调整2u使得值逐 $E[e^2(k)]$ 步达到最小，从而提高收敛性。而文献[1]则使用粒子群算法优化能力，使得 $E[e^2(k)]$ 每次迭代中做到最小化，实现 LMS 滤波的最优收敛效果，从而提升滤波降噪能力。

首先将收敛因子u设为搜索空间内的粒子，那么对 u的调整操作就转换为寻找粒子在空间的最优位置。

根据式（7），本文设定适应度函数，如下式（8）
$\tag{8}$
该适应度函数能够实现瞬时误差的最小化，从而是最小均方差 MSE达到最小。

4.PSO—LMS算法实验

利用正弦信号加噪声生成模拟数据，数据如下图所示：

在这里插入图片描述

经过原始LSM和PSO-LSM滤波后的对比图如下并且利用绝对误差和做为评价标准：
在这里插入图片描述

在这里插入图片描述

从结果上来看改进后的LMS明显优于基础LMS滤波，滤波后的信号更接近原始信号，误差更小。

5.SSA—LMS算法实验

根据同样的原理利用麻雀搜索算法对LMS滤波算法进行改进

麻雀搜索算法的具体原理参考博客：https://blog.csdn.net/u011835903/article/details/108830958。

测试结果如下：

在这里插入图片描述

可以看到麻雀搜索算法对LMS滤波的提升仍然是比较明显的。

同时运行PSO-LMS和SSA-LMS得到如下结果：

在这里插入图片描述

可以看到SSA-LMS的效果更好，误差和更小。

6.参考文献

[1]赵轶骁,汪镭.基于粒子群的LMS算法在信号滤波降噪中的应用[J].微型电脑应用,2017,33(09):71-74.

7.Matlab代码

基于粒子群的LMS滤波算法
基于麻雀搜索算法的LMS滤波算法
个人资料介绍