自适应t分布与黄金正弦改进的麻雀搜索算法
文章目录
摘要:针对麻雀搜索算法存在的容易陷入局部最优、收敛速度慢等问题,提出一种基于自适应t分布与黄金正弦改进的麻雀搜索算法(t-GSSA)。首先,通过黄金正弦算法改进发现者的位置更新方式,增强算法局部开发和全局探索能力,并且提高算法的收敛能力;其次,利用自适应t分布变异方法,对个体位置进行扰动,提升算法跳出局部最优的能力;
1.麻雀优化算法
基础麻雀算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/108830958
2. 改进麻雀算法
2.1 黄金正弦策略
Golden-SA 是受到正弦函数的启发, 利用数学 中的正弦函数进行迭代寻优, 具有较强的全局搜索 能力。同时在位置更新过程中引入黄金分割系数来 使算法能够对局部区域进行充分搜索, 使全局搜索 和局部开发能力达到良好的平衡。Golden-SA 的核 心是其位置更新公式, 首先随机产生 s s s 个个体, 第 i ( i = 1 , 2 , 3 ⋯ , s ) i(i=1,2,3 \cdots, s) i(i=1,2,3⋯,s) 个个体第 t t t 次迭代中在 d d d 维解空间 的位置为 X i t = ( X i 1 , X i 2 ⋯ X i d ) , P i t = ( P i 1 , P i 2 ⋯ P i d ) X_i^t=\left(X_{i 1}, X_{i 2} \cdots X_{i d}\right), P_i^t=\left(P_{i 1}, P_{i 2} \cdots P_{i d}\right) Xit=(Xi1,Xi2⋯Xid),Pit=(Pi1,Pi2⋯Pid) 表示第 t t t 代个体 i i i 的最优位置。然后利用公式(4)对每 个个体进行更新:
X i t + 1 = X i t × ∣ sin ( R 1 ) ∣ + R 2 × sin ( R 1 ) × ∣ x 1 × P i t − x 2 × X i t ∣ (4) X_i^{t+1}=X_i^t \times\left|\sin \left(R_1\right)\right|+R_2 \times \sin \left(R_1\right) \times\left|x_1 \times P_i^t-x_2 \times X_i^t\right| \tag{4} Xit+1=Xit×∣sin(R1)∣+R2×sin(R1)×∣
∣x1×Pit−x2×Xit∣
∣(4)
其中, R 1 ∈ [ 0 , 2 π ] R_1 \in[0,2 \pi] R1∈[0,2π] 是决定下次迭代中个体的移动距 离的一个随机数, , R 2 ∈ [ 0 , π ] R_2 \in[0, \pi] R2∈[0,π] 是决定下次移动方向 的随机数。 x 1 = − π + ( 1 − τ ) ∗ 2 π 、 x 2 = − π + τ ∗ x_1=-\pi+(1-\tau) * 2 \pi 、 x_2=-\pi+\tau * x1=−π+(1−τ)∗2π、x2=−π+τ∗ 2 π 2 \pi 2π 是根据黄金分割系数 τ ( τ = ( 5 − 1 ) / 2 ) \tau(\tau=(\sqrt{5}-1) / 2) τ(τ=(5−1)/2) 得到的 系数, 这些系数缩小了算法的搜索空间, 引领个体 逐渐去向最优值。
根据 S S A \mathrm{SSA} SSA 算法发现者位置更新公式可知, 当 R 2 < S T R_2<S T R2<ST 时, 发现者的每一维都在变小, 当 R 2 ≥ S T R_2 \geq S T R2≥ST 时, 发现者会按照正态分布随机移动到当前位置。 这样一来算法在迭代初就有向全局最优解靠近的 趋势, 容易导致算法出现早熟收敛, 陷入局部最优。因此, 本文引入 Golden-SA 改进 SSA 中发现者的位 置更新公式, 改进后的位置更新方式如公式 (5) 所 示:
{ X i , j t + 1 = X i j t × ∣ sin ( R 1 ) ∣ + R 2 × sin ( R 1 ) × ∣ x 1 × X best t − x 2 × X i j t ∣ , R 2 < S T X i , j t + Q ⋅ L , R 2 ≥ S T (5) \left\{\begin{array}{c} X_{i, j}^{t+1}= X_{i j}^t \times\left|\sin \left(R_1\right)\right|+R_2 \times \sin \left(R_1\right) \times \left|x_1 \times X_{\text {best }}^t-x_2 \times X_{i j}^t\right|, R_2<S T \\ X_{i, j}^t+Q \cdot L, \quad R_2 \geq S T \end{array}\right.\tag{5} {
Xi,jt+1=Xijt×∣sin(R1)∣+R2×sin(R1)×∣
∣x1×Xbest t−x2×Xijt∣
∣,R2<STXi,jt+Q⋅L,R2≥ST(5)
改进后的位置更新公式中, 一方面, 在每一次 迭代时麻雀个体都会与最优个体进行信息交流, 以 便充分利用当前最优解的信息, 改善了原算法中缺 乏个体间信息交流的缺陷;另一方面, 针对原算法 容易陷入局部最优的问题, Golden-SA 的引入可以 在一定程度上扩大搜索空间, 从而提升算法的全局 寻优能力; 同时, 黄金分割系数逐步缩小了搜索空 间, 并通过 R 1 R_1 R1 和 R 2 R_2 R2 控制麻雀的搜索距离和方向, 优 化了 SSA 算法的寻优方式, 进一步协调了算法的全 局探索和局部开发能力。
2.2 自适应 t 分布和动态选择策略
标准高斯分布和柯西分布是 t \mathrm{t} t 分布的两个边界 特例分布 [ 7 ] { }^{[7]} [7], 三者的函数图像如图 1 所示。本文采 用以迭代次数iter为 t \mathrm{t} t 分布的自由度参数的 t \mathrm{t} t 分布 变异算子对麻雀位置进行扰动, 使得算法在迭代前 期具有较好的全局开发能力, 在迭代后期具有良好 的局部探索能力, 并提高算法的收敛速度, 具体的 位置更新方式如下:
X i t + 1 = X i t + X i t ⋅ t ( iter ) (6) X_i^{t+1}=X_i^t+X_i^t \cdot t(\text { iter })\tag{6} Xit+1=Xit+Xit⋅t( iter )(6)
其中, X i t + 1 X_i^{t+1} Xit+1 为扰动后麻雀的位置, X i t X_i^t Xit 为麻雀 i i i 第 t t t 次 迭代时位置。所提更新公式在 X i t X_i^t Xit 的基础上, 增加了 随机干扰项 X i t ⋅ t ( X_i^t \cdot t( Xit⋅t( iter ) ) ), 既充分利用了当前位置信 息, 又增加了随机干扰信息, 有利于算法跳出局部 最优。而随着迭代次数iter增加, t \mathrm{t} t 分布逐渐向高斯 分布靠拢, 有利于增强算法的收敛速度。
自适应 t \mathrm{t} t 分布变异算子的引入, 虽然能够很大 程度上提升算法的寻优性能, 但是若无差别的对每 次迭代中的所有个体使用, 一方面会增加算法的计 算时间, 另一方面不利于发挥原算法本身的特点。 因此, 本文采用动态选择概率 p p p 来调节自适应 t \mathrm{t} t 分布 变异算子的使用。其计算公式如下:
p = w 1 − w 2 × ( maxiter − iter ) / maxiter (7) p=w_1-w_2 \times(\text { maxiter }-\text { iter }) / \text { maxiter } \tag{7} p=w1−w2×( maxiter − iter )/ maxiter (7)
其中, maxiter为最大迭代次数, iter为当前迭代次 数, w 1 w_1 w1 决定了动态选择概率的上限, w 2 w_2 w2 决定了动态 选择概率的变化幅度, 本文经过反复试验发现当 w 1 = 0.5 、 w 2 = 0.1 w_1=0.5 、 w_2=0.1 w1=0.5、w2=0.1 时, 调节作用最优。动态选择概 率 p p p 使得算法在迭代前期有较大概率于利用自适应 t \mathrm{t} t 分布变异算子对麻雀的位置进行扰动, 改善原算 法在迭代初期就存在收敛于最优解得倾向; 同时在 迭代后期, 充分发挥原算法良好的局部开发能力, 并以较小概率的 t \mathrm{t} t 分布变异作为补充, 提升算法的 收敛速度。
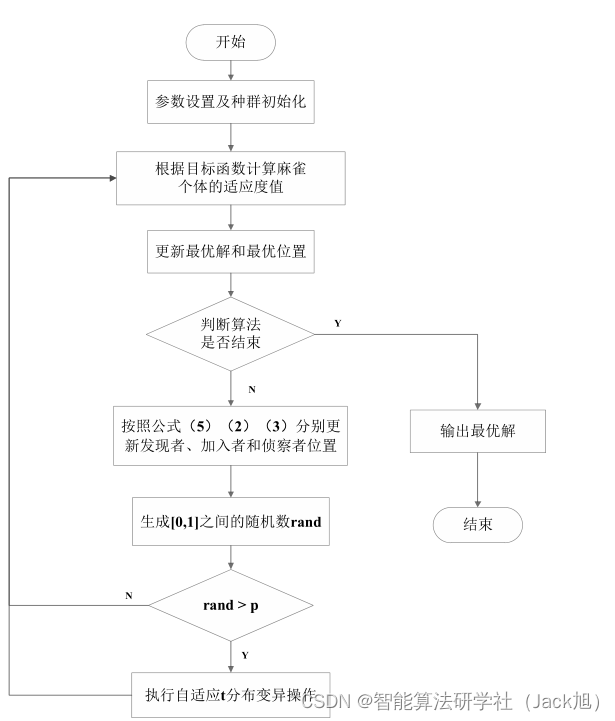
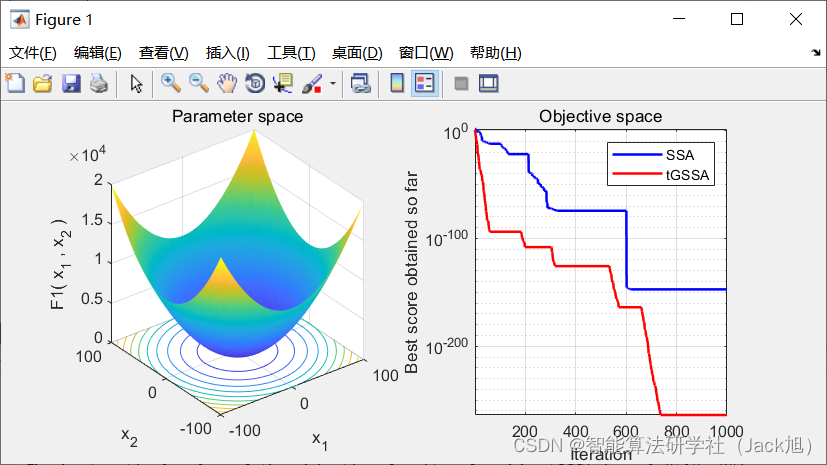
3.实验结果
4.参考文献
[1]张伟康,刘升.自适应t分布与黄金正弦改进的麻雀搜索算法及其应用[J/OL].微电子学与计算机:1-8[2021-12-17].https://doi.org/10.19304/J.ISSN1000-7180.2020-0026.