前言
Barbalat引理在非线性系统的分析中引用广泛,本博文提供相应的证明。
一、Barbalat 引理
(Barbalat 引理)
如果可微函数 f ( t ) f(t) f(t), 当 t → ∞ t \rightarrow \infty t→∞ 时存在有限极限, 且 f ˙ ( t ) \dot{f}(t) f˙(t) 一致连续, 那么当 t → ∞ t \rightarrow \infty t→∞ 时, f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0。
二、反证法
证明(反证法):
假设当 t → ∞ t \rightarrow \infty t→∞ 时, f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0 不成立,那么存在一个递增无穷序列 { t n } n ∈ N \{t_n\}_{n\in\mathbb{N}} {
tn}n∈N 使得(1)当 n → ∞ n \rightarrow \infty n→∞ 有 t n → ∞ t_n \rightarrow \infty tn→∞ ;(2) ∣ f ˙ ( t n ) ∣ ⩾ ϵ > 0 |\dot{f}(t_n) | \geqslant \epsilon>0 ∣f˙(tn)∣⩾ϵ>0 对于所有 { t n } \{t_n\} {
tn}。
考虑 f ˙ ( t ) \dot{f}(t) f˙(t) 的一致连续性,根据 ϵ − δ \epsilon-\delta ϵ−δ 理论,存在某个 ϵ > 0 \epsilon>0 ϵ>0 ,使得对于所有 n ∈ N n\in\mathbb{N} n∈N 和 所有 t ∈ R t \in \mathbb{R} t∈R,当
∣ t n − t ∣ ⩽ δ |t_n -t|\leqslant\delta ∣tn−t∣⩽δ则有 ∣ f ˙ ( t n ) − f ˙ ( t ) ∣ ≤ ϵ 2 \left|\dot{f}\left(t_{n}\right)-\dot{f}(t)\right| \leq \frac{\epsilon}{2}
f˙(tn)−f˙(t)
≤2ϵ
考虑 f ˙ ( t n ) \dot f(t_n) f˙(tn)的值和上式,可以知道 f ˙ ( t n ) \dot{f}\left(t_{n}\right) f˙(tn)和 f ˙ ( t ) \dot{f}(t) f˙(t)一定是同符号。
因此,对于所有 t ∈ [ t n , t n + δ ] t\in[t_n,t_n+\delta] t∈[tn,tn+δ],和所有 n ∈ N n\in\mathbb{N} n∈N,有 ∣ f ˙ ( t ) ∣ = ∣ f ˙ ( t n ) − ( f ˙ ( t n ) − f ˙ ( t ) ) ∣ ⩾ ∣ f ˙ ( t n ) ∣ − ∣ f ˙ ( t n ) − f ˙ ( t ) ∣ ⩾ ϵ − ϵ 2 = ϵ 2 \begin{aligned} |\dot{f}(t)| =\left|\dot{f}\left(t_{n}\right)-\left(\dot{f}\left(t_{n}\right)-\dot{f}(t)\right)\right| \geqslant \left|\dot{f}\left(t_{n}\right)\right|-\left|\dot{f}\left(t_{n}\right)-\dot{f}(t)\right| \geqslant \epsilon-\frac{\epsilon}{2}=\frac{\epsilon}{2} \end{aligned} ∣f˙(t)∣= f˙(tn)−(f˙(tn)−f˙(t)) ⩾ f˙(tn) − f˙(tn)−f˙(t) ⩾ϵ−2ϵ=2ϵ因此,对于所有 n ∈ N n\in\mathbb{N} n∈N,有 ∣ ∫ 0 t n + δ f ˙ ( t ) d t − ∫ 0 t n f ˙ ( t ) d t ∣ = ∣ ∫ t n t n + δ f ˙ ( t ) d t ∣ = ∫ t n t n + δ ∣ f ˙ ( t ) ∣ d t ≥ ϵ δ 2 > 0 \left|\int_{0}^{t_{n}+\delta} \dot{f}(t) d t-\int_{0}^{t_{n}} \dot{f}(t) d t\right|=\left|\int_{t_{n}}^{t_{n}+\delta} \dot{f}(t) d t\right|=\int_{t_{n}}^{t_{n}+\delta}|\dot{f}(t)| d t \geq \frac{\epsilon \delta}{2}>0 ∫0tn+δf˙(t)dt−∫0tnf˙(t)dt = ∫tntn+δf˙(t)dt =∫tntn+δ∣f˙(t)∣dt≥2ϵδ>0
可微函数 f ( t ) f(t) f(t), 当 t → ∞ t \rightarrow \infty t→∞ 时存在有限极限,因此可知, ∫ 0 ∞ f ˙ ( t ) d t < β \int_0^\infty \dot f(t) dt<\beta ∫0∞f˙(t)dt<β 存在,因此,当 n → ∞ n\rightarrow \infty n→∞, ∣ ∫ 0 t n + δ f ˙ ( t ) d t − ∫ 0 t n f ˙ ( t ) d t ∣ → 0 , \left|\int_{0}^{t_{n}+\delta} \dot{f}(t) d t-\int_{0}^{t_{n}} \dot{f}(t) d t\right| \rightarrow 0, ∫0tn+δf˙(t)dt−∫0tnf˙(t)dt →0,和上式产生矛盾,因此反证法可证,当 t → ∞ t \rightarrow \infty t→∞ 时, f ˙ ( t ) → 0 \dot{f}(t) \rightarrow 0 f˙(t)→0。
三、连续和一致连续
什么是一致连续,和连续的区别是什么
一致的意思是“统一”
epsilon - sigma 对某点连续定义:

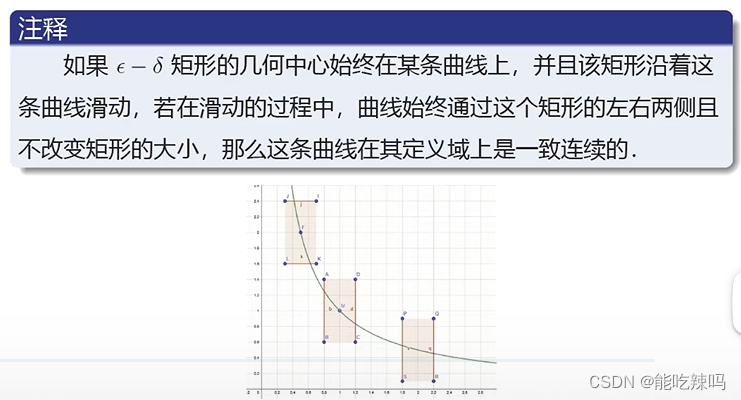
一致连续

四、Cauchy数列

https://www.bilibili.com/video/BV1cP4y1b7Fn/?spm_id_from=333.788.recommend_more_video.-1&vd_source=5138fcb56aada2b6f1c51dfff686251a