消费与储蓄的决定-中国视角下的宏观经济

消费与储蓄的决定 – 潘登同学的宏观经济学笔记

中国消费不足、储蓄过剩的事实

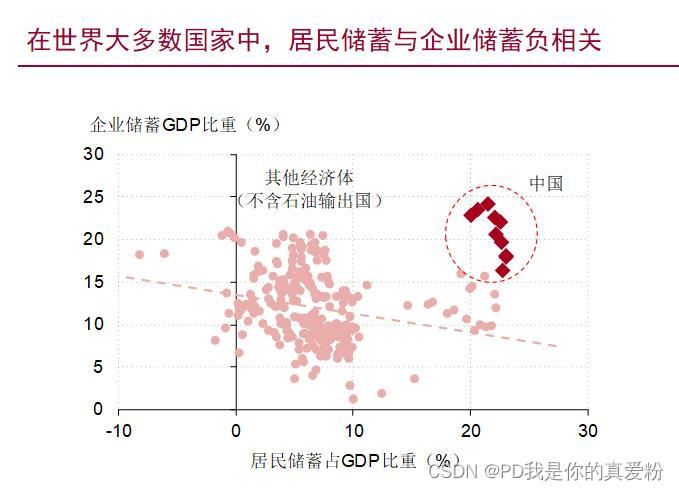
有关中国经济需求面的关键问题

• 不包含价值判断的对客观事实的陈述（实然）
  • 中国的居民消费占GDP比重明显低于世界平均水平
  • 中国的储蓄率明显高于世界平均水平
• 价值判断（应然）
  • 中国的居民消费（占比）是不是太低？
  • 中国的储蓄率是否太高？
  • 中国是否存在消费不足、储蓄过剩的现象？
  • 中国的消费与储蓄占比是否合适？

关键问题：中国消费占比应该是多少？中国的储蓄率应该是多少？

• 判断这个“应该”的标准又是什么？

拉姆齐模型

单期单个消费者的优化问题

单期的消费者偏好可以写成
$$U=u(c_1)+\delta u(c_2)$$
$\delta$表示消费者的主观贴现因子，反映了居民缺乏耐心的倾向。

以消费品为计价物写出第1期和第2期居民的预算约束
$$\begin{gathered} c_1+k_1\le k_0+r_1{k}_0+w_{1}L \\ {c}_2\le k_1+r_2{k}_1+w_{2}L \end{gathered}$$
其中，$k$为资本存量(可以理解为财富),$r$为资本回报率，$w$为工资率， $L$为居民可向外提供的劳动量。 为了简化，我们假设资本不会折旧，并且居民每期都会无弹性地将所有劳动力提供出去。 显然，居民效用最大化时，约束条件中的不等号一定会取等号。所以居民的优化问题写为
$$\begin{array}{rl}\underset{c_1,c_2,k_1}{\max }& u(c_1)+\delta u(c_2)\\ s.t.& c_1+k_1=k_0+r_1{k}_0+w_{1}L\\ & c_2=k_1+r_2{k}_1+w_{2}L\\ \Rightarrow L& =u(c_1)+\delta u(c_2)+{\lambda }_1(k_0+r_1{k}_0+w_{1}L-c_1-k_1)+{\lambda }_2(k_1+r_2{k}_1+w_{2}L-c_2)\\ FOC:& \{\begin{array}{l}\frac{\partial L}{\partial c_1}=0\Rightarrow u^{\prime }(c_1)={\lambda }_1\\ \frac{\partial L}{\partial c_2}=0\Rightarrow \delta u^{\prime }(c_2)={\lambda }_2\\ \frac{\partial L}{\partial k_1}=0\Rightarrow -{\lambda }_1+(1+r_2){\lambda }_2=0\end{array}\Rightarrow u^{\prime }(c_1)=\delta u^{\prime }(c_2)(1+r_2)\end{array}$$
这是居民跨期优化的最优条件，也称为欧拉方程。这个方程左边$u^{\prime }(c_1)$表示了把第1期的消费增加1单位，居民总效用在边际上增加的幅度。 等式右边$\delta u^{\prime }(c_2)(1+r_2)$表示把第1期的1单位产品储蓄起来留待第2期消费，居民总效用提升的幅度。

从欧拉方程来看，居民的消费与储蓄取决于两个东西。

• 一个是居民两期之间的边际效用比$\frac{u^{\prime }(c_1)}{\delta u^{\prime }(c_2)}$,它代表了居民的主观偏好。
• 另一个是储蓄回报率$1+r_2$,它代表了居民面对的客观环境。

单期多个消费者的优化问题

仅居民积累资本

一般均衡中，求解多个消费者的优化等价于求解中央计划者的优化问题。

基本假设：

• 居民总数量被正规化为1；
• 企业并不拥有资本和劳动力两种生产要素；
• 企业处于完全竞争状态，且只存在一期(期末把所有资本返还给消费者);

时间下标对应着变量取值被决定的时期，动态宏观模型中内生变量总能被划分为两类

1. 控制变量： 取值在当期决定(如消费，工资率)
2. 前定变量: 取值在上一期决定(如资本需求(由上一期的资本供给决定))

那么每一期企业的最优化问题为
$$\begin{gathered} \underset{k_{t-1}^d,l_t^d}{\max }AF(k_{t-1}^d,l_t^d)-(1+r_t)k_{t-1}^d-w_t{l}_t^{d}t=1,2 \\ FOC:\{\begin{array}{l}A{F}_1(k_{t-1}^d,l_t^d)=(1+r_t)\\ A{F}_2(k_{t-1}^d,l_t^d)=w_t\end{array} \\ 市场出清：\{\begin{array}{l}{l}_1^d=l_2^d=L\\ k_0^d=k_0\\ k_1^d=k_1\end{array} \\ 代入一阶条件：\{\begin{array}{l}A{F}_1(k_0,L)=(1+r_1)\\ A{F}_1(k_1,L)=(1+r_2)\\ A{F}_2(k_0,L)=w_1\\ A{F}_2(k_1,L)=w_2\end{array} \end{gathered}$$
将上式代入欧拉方程中，可得
$$u^{\prime }(c_1)=\delta u^{\prime }(c_2)A{F}_1(k_1,L)$$
结合消费者的预算约束
$$\{\begin{array}{l}{c}_1+k_1=AF(k_0,L)\\ c_2=AF(k_1,L)\end{array}$$
结合上面三条等式，三个未知数$(c_1,c_2,k_1)$随之被确定。

可以看出仅居民积累资本时，一般均衡与居民自己储蓄消费的均衡结果几乎一样；在仅居民积累资本下，客观世界的投资回报率就由居民的主观偏好决定

仅企业积累资本

假设企业长期存在(在两期模型中存活两期)，企业拥有资本，也负责做资本积累的决策。 为了简化，居民就不再积累任何资本；

因为企业拥有资本，所有会有正的利润(资本回报被企业所有)。所以，在这个模型中，企业产权归属必须被清晰地设定出来。因为谁拥有企业，谁就拥有企业的利润。 我们这里假设企业被居民所有，其股份由居民所持有。

• 企业拥有经济中所有的初始资本$k_0$；
• 而居民拥有企业的所有股份$s_0=1$(股份总量被正规化为1)；
• 居民仍然拥有劳动力禀赋L；

• 在第一期，企业每股分红$d_1$,居民在第1期收到的红利总量为$s_0{d}_1$
• 在第一期红利支付后，居民可以交易自己手中的企业股权(此时股价为$v_1$),从而将自己的股份持有量变为$s_1$
• 在第二期，居民获得红利支付为$s_1{d}_2$,在第二期后，企业股价变为0；

居民的优化问题可以写为
$$\begin{array}{rl}\underset{c_1,c_2,s_1}{\max }& u(c_1)+\delta u(c_2)\\ c_1+v_1{s}_1& =w_{1}L+d_1{s}_0+v_1{s}_0\\ c_2& =w_{2}L+d_2{s}_1+0\cdot s_2\\ \Rightarrow L& =u(c_1)+\delta u(c_2)+{\lambda }_1(w_{1}L+d_1{s}_0+v_1{s}_0-c_1-v_1{s}_1)\\ FOC:& \{\begin{array}{l}\frac{\partial L}{\partial c_1}=0\Rightarrow u^{\prime }(c_1)={\lambda }_1\\ \frac{\partial L}{\partial c_2}=0\Rightarrow \delta u^{\prime }(c_2)={\lambda }_2\\ \frac{\partial L}{\partial s_1}=0\Rightarrow -{\lambda }_1{v}_1+{\lambda }_2{d}_2=0\end{array}\Rightarrow v_1=\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}{d}_2\end{array}$$
上式可以视为资产定价的表达式，$\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}$是随机贴现因子；随机贴现因子虽然包含了不可观测的居民的主观偏好，但是这种主观偏好可以通过资产价格反映；

关键是企业第一期的分红如何决定

• 企业选择合适的分红来最大化它分红前的股票价值，也就是$d_1+v_1$。
• 因为如果不这样，拥有企业所有权的居民就会罢免管理层；

根据上面最优化得出的结论,有
$$d_1+v_1=d_1+\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}{d}_2$$

因此企业的最优化问题可以写成
$$\begin{array}{rl}\underset{l_1^d,l_2^d,d_1,d_2,k_1}{\max }& d_1+\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}{d}_2\\ s.t.& d_1+k_1\le AF(k_0,l_1^d)-w_1{l}_1^d+k_0\\ & d_2\le AF(k_1,l_2^d)-w_2{l}_2^d+k_1\end{array}$$
将两个约束条件不等号变为等号，代入目标函数中，可得
$$\begin{array}{rl}\underset{l_1^d,l_2^d,k_1}{\max }& AF(k_0,l_1^d)-w_1{l}_1^d+k_0-k_1\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}[AF(k_1,l_2^d)-w_2{l}_2^d+k_1]\\ FOC:& \{\begin{array}{l}A{F}_2(k_0,l_1^d)=w_1\\ A{F}_2(k_0,l_2^d)=w_2\\ \delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}[1+A{F}_1(k_1,l_2^d)]=1\end{array}\end{array}$$
均衡时，有$l_1^d=l_2^d=L,s_1=s_0=1$,所以一阶条件的第三个等式化为
$$u^{\prime }(c_1)=\delta u^{\prime }(c_2)[1+A{F}_1(k_1,L)]$$
可以看出，这与居民积累资本得出的结论时一样的；

企业和居民同时积累资本

在第1期期初， 居民和企业分别拥有$k_{c0}与k_{f0}$的资本存量。假设在第1期社会初始总资本存量为非负数$k_0$.其他的与仅企业积累资本一致；

居民的优化目标函数与之前一致
$$\begin{array}{rl}\underset{c_1,c_2,k_{c1},s_1}{\max }& u(c_1)+\delta u(c_2)\\ s.t.& \{\begin{array}{l}{c}_1+k_{c1}+v_1{s}_1=(1+r_1)k_{c0}+w_{1}L+d_1{s}_0+v_1{s}_0\\ c_2=(1+r_2)k_{c1}+w_{2}L+d_2{s}_1\end{array}\\ L& =u(c_1)+\delta u(c_2)+{\lambda }_1((1+r_1)k_{c0}+w_{1}L+d_1{s}_0+v_1{s}_0-c_1-k_{c1}-v_1{s}_1)+{\lambda }_2((1+r_2)k_{c1}+w_{2}L+d_2{s}_1-c_2)\\ FOC:& \{\begin{array}{l}\frac{\partial L}{\partial c_1}=0\Rightarrow u^{\prime }(c_1)={\lambda }_1\\ \frac{\partial L}{\partial c_2}=0\Rightarrow \delta u^{\prime }(c_2)={\lambda }_2\\ \frac{\partial L}{\partial s_1}=0\Rightarrow -{\lambda }_1{v}_1+{\lambda }_2{d}_2=0\\ \frac{\partial L}{\partial k_{c1}}=0\Rightarrow -{\lambda }_1+{\lambda }_2(1+r_2)=0\end{array}\Rightarrow \{\begin{array}{l}{v}_1=\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}{d}_2\\ 1=\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}(1+r_2)\end{array}\end{array}$$
上述两式分别对应着股票和资本的定价方程，由这两个方程可以得到无套利条件： 股权收益率应该等于资本租借的收益率，即
$$\frac{d_2}{v_1}=1+r_2$$

企业的优化目标则是最大化两期分红的贴现
$$\begin{array}{rl}\underset{k_0^d,k_1^d,l_1^d,l_2^d,d_1,d_2,k_{f1}}{\max }& d_1+\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}{d}_2\\ s.t.& \{\begin{array}{l}{d}_1+k_{f1}=AF(k_{f0}+k_0^d,l_1^d)-w_1{l}_1^d-r_1{k}_0^d+k_{f0}\\ d_2=AF(k_{f1}+k_1^d,l_2^d)-w_2{l}_2^d-r_2{k}_1^d+k_{f1}\end{array}\\ \Rightarrow \underset{k_0^d,k_1^d,l_1^d,l_2^d,k_0}{\max }& [AF(k_{f0}+k_0^d,l_1^d)-w_1{l}_1^d-r_1{k}_0^d+k_{f0}-k_{f1}]+\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}[AF(k_{f1}+k_1^d,l_2^d)-w_2{l}_2^d-r_2{k}_1^d+k_{f1}]\\ FOC:& \{\begin{array}{l}\frac{\partial L}{\partial k_0^d}=0\Rightarrow A{F}_1(k_{f0}+k_0^d,l_1^d)=r_1\\ \frac{\partial L}{\partial k_1^d}=0\Rightarrow A{F}_1(k_{f1}+k_1^d,l_2^d)=r_2\\ \frac{\partial L}{\partial l_1^d}=0\Rightarrow A{F}_2(k_{f0}+k_0^d,l_1^d)=w_1\\ \frac{\partial L}{\partial l_2^d}=0\Rightarrow A{F}_2(k_{f1}+k_1^d,l_2^d)=w_2\\ \frac{\partial L}{\partial k_{f1}}=0\Rightarrow 1=\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}[A{F}_1(k_{f1}+k_1^d,l_2^d)+1]\end{array}\end{array}$$
均衡时，劳动力市场、资本市场以及股权市场出清
$$\{\begin{array}{l}{l}_1^d=l_2^d=L\\ k_0^d=k_{c0}\\ k_1^d=k_{c1}\\ s_0=s_1=1\end{array}$$

定义$k_0=k_{c0}+k_{f0},k_1=k_{c1}+k_{f1}$带回企业优化的一阶条件
$$\begin{gathered} A{F}_1(k_0,L)=r_1,A{F}_1(k_1,L)=r_2 \\ A{F}_2(k_0,L)=w_1,A{F}_2(k_1,L)=w_2 \end{gathered}$$

对于居民部门，在两期持有的企业股份数量是一样的，都为1;
$$\{\begin{array}{l}{c}_1+k_{c1}=(1+r_1)k_{c0}+w_{1}L+d_1\\ c_2=(1+r_2)k_{c1}+w_{2}L+d_2\end{array}$$
对于企业部门的资源约束可以写成
$$\{\begin{array}{l}{d}_1+k_{f1}=AF(k_0,L)-w_{1}L-r_1{k}_{c0}+k_{f0}\\ d_2=AF(k_0,L)-w_{2}L-r_2{k}_{c1}+k_{f1}\end{array}$$
将企业部门的约束代入居民部门，消去$d_1与d_2$
$$\{\begin{array}{l}{c}_1=AF(k_0,L)+k_0-k_1\\ c_2=AF(k_1,L)+k_1\end{array}$$
结合消费者的欧拉方程
$$1=\delta \frac{u^{\prime }(c_2)}{u^{\prime }(c_1)}(1+r_2)$$
三个式子，三个未知数$(c_1,c_2,k_1)$可以确定，而这个结果与前面的仅居民积累资本，仅企业积累资本的结果一样；

刺穿企业帷幕

资本即为财富，初始资本在由居民和企业拥有的两种情况下，居民消费完全相同；这一结论说明，在企业为居民所拥有时，财富在居民和企业之间的分配并不重要，因为企业会以最大化其股票价值为经营目标。

• 而由于股票价格由居民决定，所以最大化股票价值，也就间接最大化了居民的效用

刺穿企业帷幕：

• 居民与企业两部门之间的收入分配政策不影响居民的消费与储蓄决策

这也是很多宏观经济模型假设企业是短命的，在每一期都清算，因为其清算与否都不影响最终的结论；

理性预期

在前面分析中，优化问题在第一期做出，而第二期的状况(资本回报率$r_2$与工资率$w_2$)也是在第一期被决定，这样的分析方法是基于经济分析中的理性预期的应用；

想象一个农产品市场，市场中的需求有一条向下倾斜的需求曲线所表示，
$$Q_t=10-P_t$$
与一般市场不一样的是，这个农产品市场的供给具有滞后性，当前的产出在上一期决定。当前的小麦供给由之前的小麦的播种量所决定，农夫在决定究竟播种多少的时候，只能基于未来产品价格的预期。 我们将市场供给曲线写成
$$Q_t=P_{t|t-1}^e$$
$P_{t|t-1}^e$表示在$t-1$时期对第$t$期产品价格的预期。

静态预期

在静态预期中，人认为未来价格等于当前的价格。用公式来描述
$$P_{t|t-1}^e=P_{t-1}$$
将其代入供给曲线可得
$$Q_t=P_{t-1}$$
在带回需求曲线
$$P_t=10-P_{t-1}$$
这表明市场价格将形成持续震荡的态势，这便是蛛网模型所描述的现象–蛛网波动

当供给曲线与需求曲线的斜率乘积不为-1时，就会在震荡中走向收敛或者发散；但不管哪种情况，震荡都是价格运行的关键特征；

显然，静态预期这种预期的形成发生得太过简单，并不符合现实。 做静态预期的人会不断发现自己的预期是错误的，进而改变自己的预期；

理性预期

最好的预期方式就是预期等于未来情形，所以考虑理性预期的时候，我们会反其道而行之，从预期总会被未来所应验这一理性预期的条件出发，反过来推导理性预期是什么。

农夫在第$t-1$期对第$t$期价格的理性预期写作$P_{t|t-1}^e$,根据供给曲线
$$Q_t=P_{t|t-1}^e$$
由需求曲线可知，第$t$期的产品价格应该为
$$P_t=10-Q_t=10-P_{t|t-1}^e$$
由于理性预期要求预期价格与未来相符,即
$$P_t=P_{t|t-1}^e$$
代入上式，可得
$$P_{t|t-1}^e=5$$
当农夫的价格预期为5时，他的播种量也为5，在未来，5的产品供给量确实会导致产品的价格为5。于是农夫的预期就与未来发生的一致，可以说农夫精确地预期到了未来。

从这个意义上来说，“未来价格等于5”这个理性预期是自我预言的实现；

前面对理性预期的推导并没有告诉我们理性预期究竟是怎样做出的。事实上，我们也不可能知道理性预期究竟应该怎样做出。如果真有人知道怎样做出理性预期，他早就是个预言大师，相信不会再来研究经济学了。理性预期就像我们之前介绍的理性人假设一样，是帮助我们分析现实世界的思维工具。尽管现实世界中可能没有任何人具有理性预期，但在激烈的社会竞争中，那些在形成预期上老犯错的人会逐步被淘汰，从而让人群的行为逐渐向理性预期通近。因此，可以说理性预期是现实世界收敛的方向。

理性预期革命的旗手卢卡斯早就指出了这一点。卢卡斯在他1978年发表的一篇著名的资产定价文章中说了这么一段话：

就像穆思所清楚阐明的那样，理性预期这个假设（就像“效用极大化”假设一样）并不是一个“行为假设”。也就是说，它并不试图描述人们怎样理解环境、怎样学习、怎样处理信息等这些方面。
它更应该是一种结果（近似上）应该满足的性质。而这种结果是由某种未被明确设定的学习与适应过程所产生的。

储蓄的分析

因为模型假设只有两期，所以第一期有储蓄，则第一期的储蓄为
$$s=AF(k_0,L)-c_1$$
注意： 全社会的总储蓄并不等于第2期期初的资本存量$k_1$,这是因为$k_1$中的一部分来自第一期期初的资本$k_0$。储蓄等于资本的增量$k_1-k_0$。 储蓄是一个流量概念，而资本是一个存量概念。

考虑微观层面单个居民的储蓄, 其等于居民收入(工资收入、资本回报以及分红收入)减去居民消费
$$s_c^{Micro}=r_1{k}_{c0}+w_{1}L+d_1{s}_0-c_1=(k_{c1}-k_{c0})+(v_1{s}_1-v_1{s}_0)$$
从上式看出，居民的储蓄用在了两个方面： 一是增加其资本持有量，二是增加企业股份持有量；

对于宏观层面，整个居民部门持有的股份都是1，上式变形为
$$s_c=r_1{k}_{c0}+w_{1}L+d_1-c_1=k_{c1}-k_{c0}$$

再考虑企业部门的储蓄
$$s_f=AF(k_0,L)-w_{1}L-r_1{k}_{c0}-d_1=k_{f1}-k_{f0}$$
有此式可知，企业第一期的储蓄用来增加企业企业持有的资本量。企业储蓄比企业会计报表中利润口径的数据要大。在会计中，企业的资本性开支被算成企业成本，因而并不包含在企业利润中。但在经济分析中，企业的资本性开支要算在企业储蓄之中。所以，尽管企业储蓄是个不小的正数，但是可以看到中国企业部门每年都会借入大量别的部门的储蓄，这是因为企业储蓄的规模赶不上企业投资的规模；

如果将居民和企业部门的储蓄表达式相加
$$s_c+s_f=AF(k_0,L)-c_1=k_1-k_0$$

总储蓄与净储蓄

总储蓄

• 一个部门的收入减去其消费； 在前面的分析都是总储蓄

净储蓄

• 一个部门的总储蓄减去投资所得的差额

如果一个部门净储蓄为正，就说明这个部门的投资并没有将其总储蓄用完，而是留给了别的部门；

各个部门的净储蓄状况对应着金融资金的净流向–资金总是从净储蓄为正的部门流向净储蓄为负的部门

总储蓄、净储蓄的概念对国家同样适用
$$\begin{gathered} S=Y-C \\ {S}_{net}=S-I \end{gathered}$$
一个国家总储蓄与总投资之间的缺口，需要通过国际贸易及国际资本流动来填平。一个国家如果有正的净储蓄需要外借给外国，这个国家就必然在国际贸易上表现为产品和服务的净流出，因而在国际收支上形成经常账户的顺差。于是可以写出国民收入恒等式
$$CA=S-I=S_{net}$$
即经常账户等于国内净储蓄

模型与中国经济的数量对比

我们假设居民效用函数取为CRRA形式
$$U=\frac{c_1^{1-\sigma }}{1-\sigma }+\delta \frac{c_2^{1-\sigma }}{1-\sigma }$$
其中，$\sigma$是居民的相对风险厌恶系数。根据微观个体在风险下的行为，$\sigma$大概为2；$\delta$一般取0.98

定义贴现率为$\rho \triangleq \frac{1}{\delta }-1$,根据欧拉方程
$$\begin{gathered} \frac{u^{\prime }(c_1)}{u^{\prime }(c_2)}=\delta (1+r_2) \\ \Rightarrow (\frac{c_2}{c_1}{)}^{\sigma }=\frac{1}{1+\rho }(1+r_2) \\ \Rightarrow \sigma \log (1+\frac{c_2-c_1}{c_1})=-\log (1+\rho )+\log (1+r_2) \end{gathered}$$
可以近似化为
$$r_2=\sigma \frac{△c}{c}+\rho$$
其中，$\sigma =2,\rho =2\%$,而在2000-2015年中，我国人均消费平均真实增长率为7.7%; 将这些数字代入上式，可得真实利率$r_2=17.4\%$,比我们在现实观察到的真实利率高了一个数量级；

具体来说，如果这个模型是正确的，那么考虑到我国这么高的消费增长率，我国居民的储蓄应该很少才对。但是在均衡的时尤不可能不储蓄，所以必定需要一个很高的储蓄回报率。 但在现实中，我们并没有看到理论上所计算出来的这么高的利率水平。从一个角度来看，可以说是现实中的利率太低了。而从另外一个角度来看，也可以说现实中的储蓄太多了；

在学术界，中国消费数据与理论模型的差异被称为中国的“消费之谜”；