1 正则项损失
L(W)= 1 N ∑ i L i ( f ( x i , W ) , y i ) ⏟ 数据损失:模型预测需要和训练集相匹配 \underbrace{\frac{1}{N} \sum\limits_{i}L_{i}(f(x_{i},W),y_{i})}_{数据损失:模型预测需要和训练集相匹配} 数据损失:模型预测需要和训练集相匹配 N1i∑Li(f(xi,W),yi)+ λ R ( W ) ⏟ 正则损失:防止模型在训练集上学习得“太好” \underbrace{\lambda R(W)}_{正则损失:防止模型在训练集上学习得“太好”} 正则损失:防止模型在训练集上学习得“太好” λR(W)
- 损失函数L是一个与参数W有关的函数,优化的目标就是找到使损失函数L达到最优的那组参数W。
- R(W)是一个与权值有关,跟图像数据无关的函数
- 直接方法: ⅁ L ⅁ W \frac{\Game L}{\Game W} ⅁W⅁L = 0
- λ \lambda λ是一个超参数控制着正则损失在总损失中所占的比重
- λ \lambda λ = 0优化结果仅与数据损失相关
- λ \lambda λ = ∞ \infty ∞优化结果与数据损失无关,仅考虑权重损失。此时,系统最优解为W = 0。
- 常用的正则项损失
-
L1正则项:R(W) = ∑ k \sum_{k} ∑k ∑ l \sum_{l} ∑l|W k , l _{k,l} k,l|
-
L2正则项:R(W) = ∑ k \sum_{k} ∑k ∑ l \sum_{l} ∑lW k , l 2 _{k,l}^{2} k,l2
-
Elastic net(L1+L2):R(W) = ∑ k \sum_{k} ∑k ∑ l \sum_{l} ∑l β \beta βW k , l 2 _{k,l}^{2} k,l2+|W k , l _{k,l} k,l|
-
2 优化算法
2.1 什么是参数优化
利用损失函数的输出值作为反馈信号来调整分类器参数,以提升分类器对训练样本的预测性能。
2.2 梯度下降算法
- 利用所有样本计算损失并更新梯度
- 往哪走?
- 答:负梯度方向
- 走多远?
- 答:步长决定
2.2.1 梯度计算
(1) 数值法
一维变量,函数求导:
d L ( w ) d w \frac{dL(w)}{dw} dwdL(w) = lim h → 0 L ( w + h ) − L ( w ) h \lim_{h\to0} \frac{L(w+h)-L(w)}{h} limh→0hL(w+h)−L(w)
示例:损失函数L(w) = w 2 ^{2} 2 求w = 1点处的梯度
d L ( w ) d w \frac{dL(w)}{dw} dwdL(w) = lim h → 0 L ( w + h ) − L ( w ) h \lim_{h\to0} \frac{L(w+h)-L(w)}{h} limh→0hL(w+h)−L(w) ≈ L ( 1 + 0.0001 ) − L ( 1 ) 0.0001 \frac{L(1 + 0.0001) - L(1)}{0.0001} 0.0001L(1+0.0001)−L(1) = 2.0001
(2) 解析法
示例:损失函数L(w) = w 2 ^{2} 2 ,求w = 1点处的梯度
▽ \bigtriangledown ▽L(w) = 2w
▽ \bigtriangledown ▽ w = 1 _{w = 1} w=1L(w) = 2
(3) 梯度计算总结
- 数值梯度:近似,慢,易写
- 解析梯度:精确,快,易错
- 求梯度一般使用解析梯度,数值梯度主要用于解析梯度的正确性校验
- 缺点:运算量大、时间慢
2.3 随机梯度下降算法
随机梯度下降:每次随机算账一个样本x i _{i} i,计算损失并更新梯度
L(W) = L i _{i} i(x i _{i} i,y i _{i} i,W) + λ \lambda λR(W)
▽ \bigtriangledown ▽ w _{w} wL(W) = ▽ \bigtriangledown ▽ w _{w} wL i {i} i(x i _{i} i,y i _{i} i,W) + λ \lambda λ ▽ \bigtriangledown ▽ W _{W} WR(W)
while True
\qquad 数据 <- 从训练数据采样(训练数据,1)
\qquad 权值的梯度 <- 计算梯度(损失,数据,权值)
\qquad 权值 <- 权值 <- 学习率* 权值的梯度
单个样本的训练可能会带来很多噪声,不是每次迭代都向着整体最优化方向
2.4 小批量梯度下降算法
小批量随机梯度下降:每次随机选择m(批量的大小)个样本,计算损失并更新梯度
L(W) = 1 m \frac{1}{m} m1 ∑ i = 1 m \sum\limits_{i=1}^m i=1∑mL i _{i} i(x i _{i} i,y i _{i} i,W) + λ \lambda λR(W)
▽ \bigtriangledown ▽ w _{w} wL(W) = 1 m \frac{1}{m} m1 ∑ i = 1 m \sum\limits_{i=1}^m i=1∑m ▽ \bigtriangledown ▽ w _{w} wL i {i} i(x i _{i} i,y i _{i} i,W) + λ \lambda λ ▽ \bigtriangledown ▽ W _{W} WR(W)
while True
\qquad 数据 <- 从训练数据采样(训练数据,批量大小)
\qquad 权值的梯度 <- 计算梯度(损失,数据,权值)
\qquad 权值 <- 权值 <- 学习率* 权值的梯度
3 数据集划分
3.1 划分1
数据集:所有带标签数据
- 训练集 -> 训练模型 -> 寻找最优分类器
- 测试集 -> 评估模型 -> 评测泛化能力
3.2 划分2
数据集:所有带标签数据
- 训练集 :给定的超参数时分类器参数的学习
- 验证集:用于选择超参数
- 测试集:评估泛化能力
4 K折交叉验证
拟解决问题:如果数据很少,那么可能验证集包含的样本就太少,从而无法在统计上代表数据。
发现该问题:如果在划分数据前进行不同的随机打乱,最终得到的模型性能差别很大,那么就存在这个问题。
接下来会介绍K折验证与重复的K折验证,它们是解决这一问题的两种方法。
4.1 3折验证
除训练集外的所有样本
第1折 验证 | 训练 | 训练 ->第1个验证分数 --|
第2折 训练 | 验证 | 训练 ->第2个验证分数 |-最终分数取平均
第3折 训练 | 训练 | 验证 ->第3个验证分数 --|
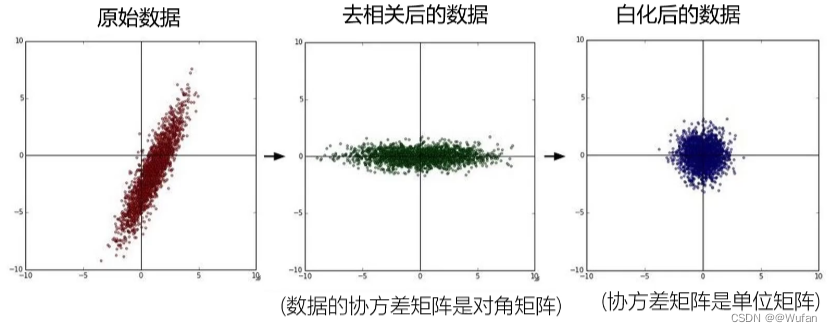
5 数据预处理
数据预处理 1

数据预处理 2