一、理论基础
1、麻雀搜索算法
请参考这里。
2、GSSA搜索算法
(1)佳点集
佳点集是由我国数学家华罗庚等提出,其原理为:设 G s G_s Gs是 s s s维欧氏空间中的单位立方体,如果 r ∈ G s r\in G_s r∈Gs,形为: P n ( k ) = { ( { r 1 ( n ) ⋅ k } , { r 2 ( n ) ⋅ k } , ⋯ , { r s ( n ) ⋅ k } ) , 1 ≤ k ≤ n } (1) P_n(k)=\left\{\left(\left\{r_1^{(n)}\cdot k\right\},\left\{r_2^{(n)}\cdot k\right\},\cdots,\left\{r_s^{(n)}\cdot k\right\}\right),1\leq k\leq n\right\}\tag{1} Pn(k)={
({
r1(n)⋅k},{
r2(n)⋅k},⋯,{
rs(n)⋅k}),1≤k≤n}(1)其偏差 φ ( n ) \varphi(n) φ(n)满足 φ ( n ) = C ( r , ε ) n − 1 + ε \varphi(n)=C(r,\varepsilon)n^{-1+\varepsilon} φ(n)=C(r,ε)n−1+ε,其中 C ( r , ε ) n − 1 + ε C(r,\varepsilon)n^{-1+\varepsilon} C(r,ε)n−1+ε是只与 r r r和 ε \varepsilon ε( ε \varepsilon ε是任意的正数)有关的常数,则称 P n ( k ) P_n(k) Pn(k)为佳点集, r r r为佳点。 { r s ( n ) ⋅ k } \left\{r_s^{(n)}\cdot k\right\} {
rs(n)⋅k}代表取小数部分, n n n表示点数,取 r = { 2 cos ( 2 π k / p ) , 1 ≤ k ≤ s } r=\left\{2\cos(2\pi k/p),1\leq k\leq s\right\} r={
2cos(2πk/p),1≤k≤s}( p p p是满足 ( p − 3 ) / 2 ≥ s (p-3)/2\geq s (p−3)/2≥s的最小素数)。将其映射到搜索空间为: x i ( j ) = ( u b j − l b j ) ⋅ { r j ( i ) ⋅ k } + l b j (2) x_i(j)=(ub_j-lb_j)\cdot\left\{r_j^{(i)}\cdot k\right\}+lb_j\tag{2} xi(j)=(ubj−lbj)⋅{
rj(i)⋅k}+lbj(2) u b j ub_j ubj和 l b j lb_j lbj表示第 j j j维的上下界。
图1.(a)为佳点集在 [ 0 , 1 ] [0,1] [0,1]内的种群个数为500,维度为1时的随机生成的初始种群分布图。图1.(b)为上述条件下,佳点集和Tent混沌映的频率分布直方图。可以看出佳点集成均匀分布,且效果较Tent误差更小,在初始化过程中可增加种群的多样性,有利于摆脱局部最值的吸引。

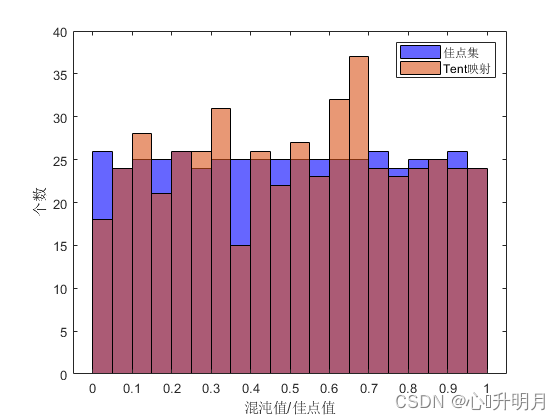
(2)改进的迭代局部搜索
局部搜索算法是从爬山法改进而来的,简单来说,是一种简单的贪心搜索算法。局部搜索从一个初始解开始,然后搜索解的邻域,如有更优的解则更新该解,否则返回当前解。迭代局部搜索(Iterative Local Search, ILS)则是在局部搜索得到的局部最优解上,加入扰动再重新进行局部搜索,具有一定的探索性。
改进后的迭代局部搜索,共有三次修改过程,即第一次修改采用SSA方法(采取当 i < N / 2 i<N/2 i<N/2时,SSA算法的加入者具有向发现者最优解快速靠拢的独特更新机制进行扰动)进行扰动,使个体跳跃到当前全局最优位置的附近,用来跳出局部最优;第二次修改采用ILS方法,即对初始解和扰动后中间解进行局部搜索,以期稳定的优化结果,提升局部搜索的精度;第三次修改利用贪婪策略对初始解和中间解局部搜索后的局部解1和2进行比较,选取较优值作为最终解 X X X,以期获得最优的局部搜索结果,保证解的质量。改进后的迭代局部搜索既充分利用了当前个体的位置信息,又充分利用了当前最优解的位置信息,寻优更加灵活。
算法流程如下:
Step 1:借助当前最优解 X b e s t X_{best} Xbest对初始解 X ∗ X^* X∗进行扰动,得到中间解 X ∗ ∗ X^{**} X∗∗,扰动公式如下: X ∗ ∗ = X b e s t + ∣ X ∗ − X b e s t ∣ ⋅ A + ⋅ L (3) X^{**}=X_{best}+\left|X^*-X_{best}\right|\cdot A^+\cdot L\tag{3} X∗∗=Xbest+∣X∗−Xbest∣⋅A+⋅L(3)原SSA加入者公式如下: x i , j t + 1 = x P t + 1 + ∣ x i , j t − x P t + 1 ∣ ⋅ A + ⋅ L , i < N 2 (4) x_{i,j}^{t+1}=x_P^{t+1}+\left|x_{i,j}^t-x_P^{t+1}\right|\cdot A^+\cdot L,\quad i<\frac N2\tag{4} xi,jt+1=xPt+1+∣∣xi,jt−xPt+1∣∣⋅A+⋅L,i<2N(4)其中 X b e s t X_{best} Xbest为 x P t + 1 x_P^{t+1} xPt+1,表示发现者当前所占据的最佳位置; X ∗ X^* X∗为 x i , j t x_{i,j}^t xi,jt,即麻雀的当前位置; X ∗ ∗ X^{**} X∗∗为 x i , j t + 1 x_{i,j}^{t+1} xi,jt+1,即更新完后的位置。
Step 2:对初始解 X ∗ X^* X∗进行局部搜索,公式如下: X 1 = X ∗ ⋅ rand ( ) (5) X^1=X^*\cdot\text{rand}()\tag{5} X1=X∗⋅rand()(5)其中, rand ( ) \text{rand}() rand()是一个属于0到1之间的随机数。
Step 3:对中间解 X ∗ ∗ X^{**} X∗∗进行局部搜索,公式如下: X 2 = X ∗ ∗ ⋅ rand() (6) X^2=X^{**}\cdot\text{rand()}\tag{6} X2=X∗∗⋅rand()(6)Step 4:计算 X 1 X^1 X1的适应度 f ( X 1 ) f(X^1) f(X1)。
Step 5:计算 X 2 X^2 X2的适应度 f ( X 2 ) f(X^2) f(X2)。
Step 6:比较 f ( X 1 ) f(X^1) f(X1)和 f ( X 2 ) f(X^2) f(X2),选择较优的个体进行位置更新,即: X = { X 1 , f ( X 1 ) ≤ f ( X 2 ) X 2 , f ( X 1 ) > f ( X 2 ) (7) X=\begin{dcases}X^1,\quad f(X^1)\leq f(X^2)\\[2ex]X^2,\quad f(X^1)>f(X^2)\end{dcases}\tag{7} X=⎩⎨⎧X1,f(X1)≤f(X2)X2,f(X1)>f(X2)(7)根据SSA算法和上述三次的修改,将SSA算法中 i < N / 2 i<N/2 i<N/2的加入者公式更新如下: x i , j t + 1 = { x i , j t ⋅ rand() , i < N 2 and f ( X 1 ) ≤ f ( X 2 ) ( x P t + 1 + ∣ x i , j t − x P t + 1 ∣ ⋅ A + ⋅ L ) ⋅ rand ( ) , i < N 2 and f ( X 1 ) > f ( X 2 ) (8) x_{i,j}^{t+1}=\begin{dcases}x_{i,j}^t\cdot\text{rand()},\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad i<\frac N2\,\,\text{and}\,\,f(X^1)\leq f(X^2)\\[2ex]\left(x_P^{t+1}+\left|x_{i,j}^t-x_P^{t+1}\right|\cdot A^+\cdot L\right)\cdot\text{rand}(),\quad i<\frac N2\,\,\text{and}\,\,f(X^1)>f(X^2)\end{dcases}\tag{8} xi,jt+1=⎩⎪⎪⎨⎪⎪⎧xi,jt⋅rand(),i<2Nandf(X1)≤f(X2)(xPt+1+∣∣xi,jt−xPt+1∣∣⋅A+⋅L)⋅rand(),i<2Nandf(X1)>f(X2)(8)
(3)逐维透镜反向学习
具体原理请参考这里。将透镜成像扩展到每个维度,对每个维度进行透镜成像反向学习,公式扩展如下: x j ∗ = a j + b j 2 + a j + b j 2 k − x j k (9) x_j^*=\frac{a_j+b_j}{2}+\frac{a_j+b_j}{2k}-\frac{x_j}{k}\tag{9} xj∗=2aj+bj+2kaj+bj−kxj(9)其中, j j j为当前维度, a j a_j aj为第 j j j维的下界, b j b_j bj为第 j j j维的上界。
同时采取动态边界即: a j = min ( x j ) (10) a_j=\min(x_j)\tag{10} aj=min(xj)(10) b j = max ( x j ) (11) b_j=\max(x_j)\tag{11} bj=max(xj)(11)
(4)GSSA算法流程
GSSA算法利用佳点集初始化种群,在加入者和警戒者位置更新时分别加入了改进的迭代局部搜索和逐维透镜成像反向学习,增加了种群多样性和对当前解的利用,提升了算法摆脱局部极值吸引的能力,具有更加灵活细致的搜索性能,其具体实现步骤如下:
Step 1:设置初始化参数,包括种群规模 N N N、发现者比例 P D PD PD、警戒者比例 S D SD SD、目标函数维度 D D D、上下界 u b ub ub和 l b lb lb、最大迭代次数 T T T、安全阈值 S T ST ST、聚焦能力系数 k k k。
Step 2:利于2.1节佳点集中的式(2)初始化种群。
Step 3:计算每个个体的适应度值 f i f_i fi,对适应度排序,选出当前最优适应度值 f g f_g fg及其所对应的位置 X b e s t X_{best} Xbest,当前最差适应度值 f w f_w fw及其所对应的位置 X w o r s t X_{worst} Xworst。
Step 4:选取适应度值前 P D ⋅ N PD\cdot N PD⋅N的个体作为发现者,根据原始SSA对应公式更新其位置,并确定发现者当前所占据的最优位置 X p X_p Xp。
Step 5:选取剩下的个体作为加入者,根据原始SSA对应公式和(8)更新其位置。
Step 6:从麻雀种群中随机选取 S D ⋅ N SD\cdot N SD⋅N的个体作为警戒者,根据原始SSA对应公式和式(9)更新其位置。
Step 7:计算适应度值,更新麻雀位置和 f g f_g fg、 X b e s t X_{best} Xbest、 f w f_w fw、 X w o r s t X_{worst} Xworst。
Step 8:判断是否满足输出条件,满足则输出结果,否则重复Step 4~7。
二、仿真实验和结果分析
将GSSA与PSO、GWO、WOA和SSA进行对比,以文献[1]中表1的12个函数为例,实验设置种群规模为30,最大迭代次数为500,每种算法独立运算30次,结果显示如下:












函数:F1
PSO:最差值: 7.3866, 最优值: 1.358, 平均值: 4.6413, 标准差: 1.4714, 秩和检验: 1.2118e-12
GWO:最差值: 2.1197e-26, 最优值: 1.3501e-29, 平均值: 1.6443e-27, 标准差: 3.9147e-27, 秩和检验: 1.2118e-12
WOA:最差值: 3.1105e-69, 最优值: 1.3292e-83, 平均值: 1.0394e-70, 标准差: 5.6785e-70, 秩和检验: 1.2118e-12
SSA:最差值: 1.1193e-78, 最优值: 2.7108e-289, 平均值: 3.7309e-80, 标准差: 2.0435e-79, 秩和检验: 1.2118e-12
GSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F2
PSO:最差值: 373.4374, 最优值: 153.2352, 平均值: 250.7457, 标准差: 50.1594, 秩和检验: 1.2118e-12
GWO:最差值: 3.5847e-15, 最优值: 2.4897e-16, 平均值: 1.2551e-15, 标准差: 7.9261e-16, 秩和检验: 1.2118e-12
WOA:最差值: 7.4609e-49, 最优值: 1.1991e-56, 平均值: 5.0744e-50, 标准差: 1.7973e-49, 秩和检验: 1.2118e-12
SSA:最差值: 2.5222e-31, 最优值: 6.9196e-315, 平均值: 1.2379e-32, 标准差: 4.8349e-32, 秩和检验: 1.2118e-12
GSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F3
PSO:最差值: 9.3267, 最优值: 2.8962, 平均值: 6.0096, 标准差: 1.4524, 秩和检验: 1.2118e-12
GWO:最差值: 4.5355e-06, 最优值: 4.6881e-08, 平均值: 8.3394e-07, 标准差: 8.9061e-07, 秩和检验: 1.2118e-12
WOA:最差值: 89.4675, 最优值: 4.3858, 平均值: 44.4708, 标准差: 27.4916, 秩和检验: 1.2118e-12
SSA:最差值: 4.2463e-30, 最优值: 0, 平均值: 1.4154e-31, 标准差: 7.7526e-31, 秩和检验: 1.6572e-11
GSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F4
PSO:最差值: 1921.1445, 最优值: 197.3311, 平均值: 709.1427, 标准差: 500.7525, 秩和检验: 3.0199e-11
GWO:最差值: 28.7684, 最优值: 26.0183, 平均值: 27.0541, 标准差: 0.89066, 秩和检验: 3.0199e-11
WOA:最差值: 28.7636, 最优值: 26.9599, 平均值: 27.9967, 标准差: 0.54643, 秩和检验: 3.0199e-11
SSA:最差值: 0.00040439, 最优值: 6.969e-09, 平均值: 5.1453e-05, 标准差: 8.2019e-05, 秩和检验: 0.063533
GSSA:最差值: 0.00042144, 最优值: 4.0903e-08, 平均值: 9.2796e-05, 标准差: 0.00010634, 秩和检验: 1
函数:F5
PSO:最差值: 7.8709, 最优值: 1.7474, 平均值: 3.7399, 标准差: 1.397, 秩和检验: 3.0199e-11
GWO:最差值: 1.4933, 最优值: 0.00010514, 平均值: 0.82245, 标准差: 0.36438, 秩和检验: 3.0199e-11
WOA:最差值: 1.2028, 最优值: 0.089566, 平均值: 0.33256, 标准差: 0.21617, 秩和检验: 3.0199e-11
SSA:最差值: 4.8048e-08, 最优值: 4.5413e-12, 平均值: 9.2174e-09, 标准差: 1.2813e-08, 秩和检验: 0.0026243
GSSA:最差值: 4.0319e-07, 最优值: 1.2852e-12, 平均值: 6.7436e-08, 标准差: 9.5255e-08, 秩和检验: 1
函数:F6
PSO:最差值: -2426.1785, 最优值: -3927.0634, 平均值: -3139.168, 标准差: 407.2728, 秩和检验: 3.0199e-11
GWO:最差值: -3592.179, 最优值: -8177.7368, 平均值: -6213.893, 标准差: 837.2262, 秩和检验: 0.016955
WOA:最差值: -7491.1384, 最优值: -12569.2438, 平均值: -10452.7436, 标准差: 1835.4013, 秩和检验: 3.0199e-11
SSA:最差值: -6370.5275, 最优值: -9461.1512, 平均值: -7995.8426, 标准差: 540.5661, 秩和检验: 1.7769e-10
GSSA:最差值: -5998.3983, 最优值: -7428.0148, 平均值: -6575.7085, 标准差: 386.4233, 秩和检验: 1
函数:F7
PSO:最差值: 16.6183, 最优值: 5.0776, 平均值: 10.7029, 标准差: 3.4705, 秩和检验: 1.2118e-12
GWO:最差值: 0.029821, 最优值: 0, 平均值: 0.0048254, 标准差: 0.0093544, 秩和检验: 0.002788
WOA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
SSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
GSSA:最差值: 0, 最优值: 0, 平均值: 0, 标准差: 0, 秩和检验: NaN
函数:F8
PSO:最差值: 10.3892, 最优值: 2.5312, 平均值: 5.1028, 标准差: 2.0657, 秩和检验: 3.0199e-11
GWO:最差值: 0.082051, 最优值: 0.019747, 平均值: 0.042535, 标准差: 0.018145, 秩和检验: 3.0199e-11
WOA:最差值: 0.10545, 最优值: 0.0050238, 平均值: 0.023367, 标准差: 0.020094, 秩和检验: 3.0199e-11
SSA:最差值: 5.9463e-09, 最优值: 2.4511e-12, 平均值: 4.8034e-10, 标准差: 1.1129e-09, 秩和检验: 2.959e-05
GSSA:最差值: 9.4681e-08, 最优值: 4.261e-12, 平均值: 6.5968e-09, 标准差: 1.7597e-08, 秩和检验: 1
函数:F9
PSO:最差值: 61.2061, 最优值: 1.4565, 平均值: 18.9374, 标准差: 17.5265, 秩和检验: 3.0199e-11
GWO:最差值: 1.0268, 最优值: 0.19887, 平均值: 0.67375, 标准差: 0.23031, 秩和检验: 3.0199e-11
WOA:最差值: 1.1996, 最优值: 0.11362, 平均值: 0.54816, 标准差: 0.29715, 秩和检验: 3.0199e-11
SSA:最差值: 6.024e-08, 最优值: 5.0309e-11, 平均值: 7.6724e-09, 标准差: 1.3783e-08, 秩和检验: 0.042067
GSSA:最差值: 2.9373e-07, 最优值: 4.5184e-12, 平均值: 4.43e-08, 标准差: 7.8019e-08, 秩和检验: 1
函数:F10
PSO:最差值: 5.9288, 最优值: 0.998, 平均值: 1.4606, 标准差: 0.96109, 秩和检验: 0.88939
GWO:最差值: 10.7632, 最优值: 0.998, 平均值: 4.9144, 标准差: 4.2863, 秩和检验: 1.6822e-11
WOA:最差值: 10.7632, 最优值: 0.998, 平均值: 2.6682, 标准差: 2.9611, 秩和检验: 1.6822e-11
SSA:最差值: 12.6705, 最优值: 0.998, 平均值: 7.8821, 标准差: 5.3702, 秩和检验: 5.4849e-07
GSSA:最差值: 0.998, 最优值: 0.998, 平均值: 0.998, 标准差: 2.2395e-16, 秩和检验: 1
函数:F11
PSO:最差值: 0.020363, 最优值: 0.00030749, 平均值: 0.0035463, 标准差: 0.0068725, 秩和检验: 0.37897
GWO:最差值: 0.020363, 最优值: 0.00030751, 平均值: 0.0024633, 标准差: 0.0060747, 秩和检验: 4.6159e-10
WOA:最差值: 0.0017275, 最优值: 0.00034417, 平均值: 0.00068587, 标准差: 0.00035016, 秩和检验: 3.0199e-11
SSA:最差值: 0.00071324, 最优值: 0.00030749, 平均值: 0.00032114, 标准差: 7.4057e-05, 秩和检验: 0.80727
GSSA:最差值: 0.00030807, 最优值: 0.00030749, 平均值: 0.00030756, 标准差: 1.2731e-07, 秩和检验: 1
函数:F12
PSO:最差值: -2.4273, 最优值: -10.5364, 平均值: -8.5399, 标准差: 3.3933, 秩和检验: 0.011241
GWO:最差值: -10.5327, 最优值: -10.5362, 平均值: -10.5345, 标准差: 0.00090389, 秩和检验: 0.0019312
WOA:最差值: -1.6708, 最优值: -10.5347, 平均值: -6.9574, 标准差: 3.2899, 秩和检验: 1.3187e-07
SSA:最差值: -5.1285, 最优值: -10.5364, 平均值: -9.4548, 标准差: 2.2002, 秩和检验: 0.049697
GSSA:最差值: -5.1285, 最优值: -10.5364, 平均值: -9.4504, 标准差: 2.198, 秩和检验: 1
实验结果表明改进算法具有更好的寻优性能,算法更加稳定且收敛速度更快。
三、参考文献
[1] 闫少强, 杨萍, 朱东林, 等. 基于佳点集的改进麻雀搜索算法[J/OL]. 北京航空航天大学学报: 1-13 [2022-06-06].