sklearn机器学习（四）线性回归算法拟合正弦函数

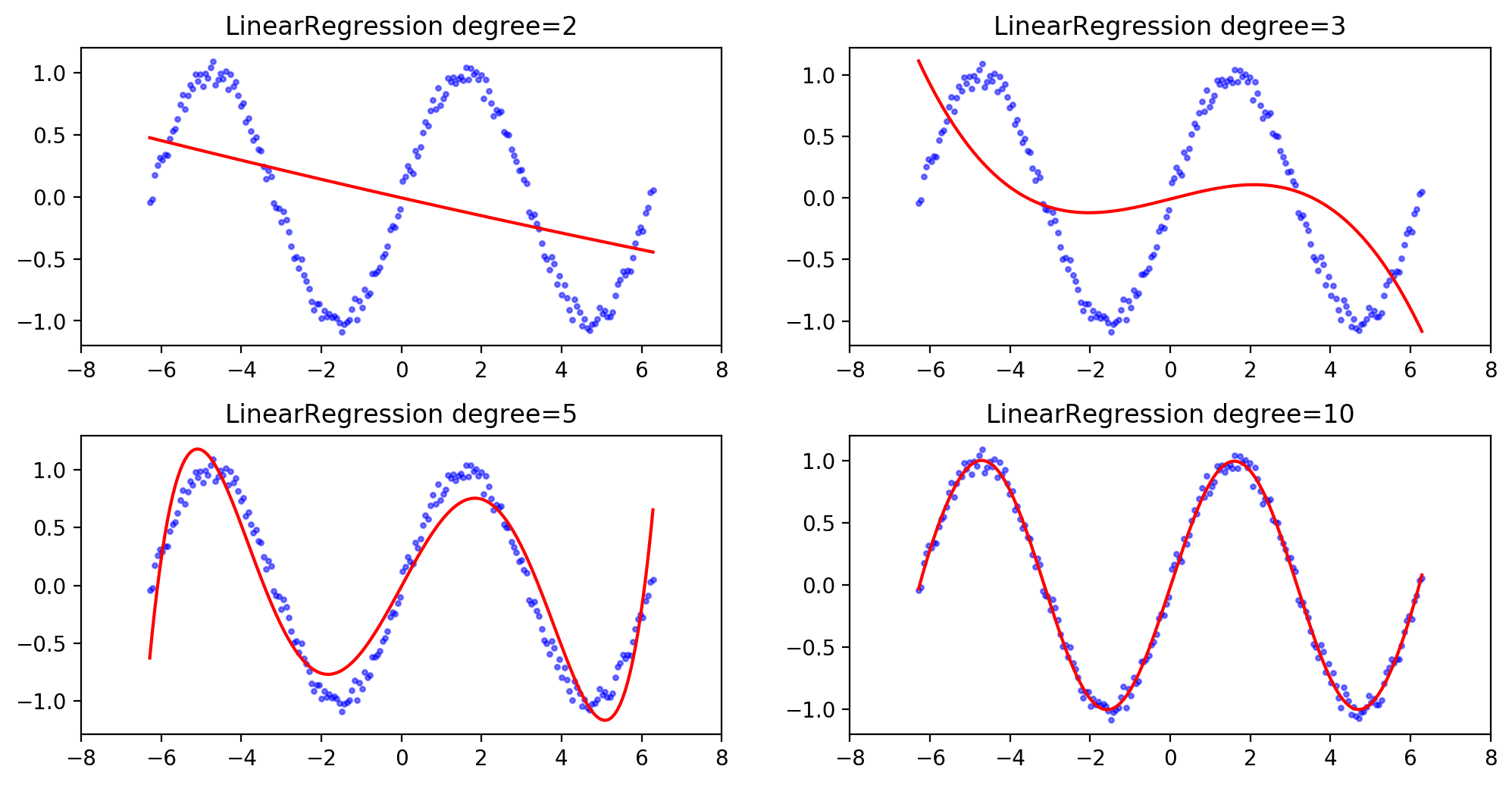
今天，我们开始使用线性回归算法来拟合正弦函数。
首先这里我们需要做的就是回顾一下学习曲线的知识，就是本系列的第一篇文章。
如果看过就不多说，没看过可以去看看。以下是链接：
https://blog.csdn.net/qq_41487299/article/details/90596990

因为下面有用到这方面的知识，所以我就不再过多赘述，会有些简洁。
第一个代码块，还是老样子，生成数据

import numpy as np
import matplotlib.pyplot as plt
n_dots=200

X=np.linspace(-2*np.pi,2*np.pi,n_dots)#生成-2*3.14到2*3.14的200个数
Y=np.sin(X)+0.2*np.random.rand(n_dots)-0.1#将X正弦化，然后加入噪音
X=X.reshape(-1,1)#扁平化，就是features只能为1
Y=Y.reshape(-1,1)

第二个代码块，就是流水线生成degree阶多项式，用设计模式的话说就是工厂模式

from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

def polynomial_model(degree=1):
    polynomial_features=PolynomialFeatures(degree=degree,include_bias=False)#生成degree阶多项式
    linear_regression=LinearRegression(normalize=True)#线性回归实例化，并且正规化
    pipeline=Pipeline([("polynomial_features",polynomial_features),("linear_regression",linear_regression)])#流水线
    return pipeline

第三代码块，就是具体的生成模型

from sklearn.metrics import mean_squared_error

degrees=[2,3,5,10]#多项式的阶数
results=[]#结果数组
for d in degrees:#运行四次
    model=polynomial_model(degree=d)#生产degree多项式模型
    model.fit(X,Y)#将X,Y扔到模型里面去训练
    train_score=model.score(X,Y)#得到评分
    mse=mean_squared_error(Y,model.predict(X))#计算均方根误差
    results.append({"model":model,"degree":d,"score":train_score,"mse":mse})#追加对应数据到results里面
for r in results:
    print("degree:{};train score:{};mean squared error:{}".format(r["degree"],r["score"],r["mse"]))

degree:2;train score:0.14228316444628064;mean squared error:0.4305736796171162
degree:3;train score:0.2653705201788461;mean squared error:0.368783851698095
degree:5;train score:0.901777344360999;mean squared error:0.04930775345332575
degree:10;train score:0.9941441892665257;mean squared error:0.0029396158150792563
上面的是第三代码块的输出。
从中我们可以看到在线性拟合中，多项式的阶数越高，其拟合的效果也就越好。
下面我将贴出results数组里面的值：

[{‘model’: Pipeline(memory=None,
steps=[(‘polynomial_features’, PolynomialFeatures(degree=2, include_bias=False, interaction_only=False)), (‘linear_regression’, LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True))]), ‘degree’: 2, ‘score’: 0.15016025416103307, ‘mse’: 0.4289391880883589}, {‘model’: Pipeline(memory=None,
steps=[(‘polynomial_features’, PolynomialFeatures(degree=3, include_bias=False, interaction_only=False)), (‘linear_regression’, LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True))]), ‘degree’: 3, ‘score’: 0.28175785775693585, ‘mse’: 0.3625179957198201}, {‘model’: Pipeline(memory=None,
steps=[(‘polynomial_features’, PolynomialFeatures(degree=5, include_bias=False, interaction_only=False)), (‘linear_regression’, LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True))]), ‘degree’: 5, ‘score’: 0.8963213564851418, ‘mse’: 0.05232966966903011}, {‘model’: Pipeline(memory=None,
steps=[(‘polynomial_features’, PolynomialFeatures(degree=10, include_bias=False, interaction_only=False)), (‘linear_regression’, LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=True))]), ‘degree’: 10, ‘score’: 0.9932882609748797, ‘mse’: 0.0033876126672023367}]

我们可以从中看出不少东西，首先是它里面的各个degree的值正好对应了对象是的阶数，还有数组中的score与mse正好与上面的输出中的score与mse相对应。说明了我们的数据不是凭空得来的

第四代码块就是绘制图形

from matplotlib.figure import SubplotParams
plt.figure(figsize=(12,6),dpi=200,subplotpars=SubplotParams(hspace=0.3))
                  #subplotpars只是控制各下属图形高度上的间距为0.3
for i,r in enumerate(results):#循环四次
    fig=plt.subplot(2,2,i+1)#四张图，绘画顺序对应i+1
    plt.xlim(-8,8)#每张图的x轴的限制为-8到8，对应上面的-2*3.14到2*3.14
    plt.title("LinearRegression degree={}".format(r["degree"]))#标题
    plt.scatter(X,Y,s=5,c='b',alpha=0.5)#蓝色的散点
    plt.plot(X,r["model"].predict(X),'r-')#预测的曲线

在这里插入图片描述
从以上结果，可以看出十阶多项式的拟合效果是最好的。只是前面进行了学习曲线的绘制的我，还是有着这么一个疑问，就是阶数越大拟合效果就更好，那13阶，15阶呢？会出现过拟合现象吗？

于是我选择将第三代码块进行了一点小小的修改。

from sklearn.metrics import mean_squared_error

degrees=[5,10,13,15]#修改这里的阶数
results=[]
for d in degrees:
    model=polynomial_model(degree=d)
    model.fit(X,Y)
    train_score=model.score(X,Y)
    mse=mean_squared_error(Y,model.predict(X))
    results.append({"model":model,"degree":d,"score":train_score,"mse":mse})
for r in results:
    print("degree:{};train score:{};mean squared error:{}".format(r["degree"],r["score"],r["mse"]))

得到的结果如下：
degree:5;train score:0.8982314289785879;mean squared error:0.05033878673813532
degree:10;train score:0.9931102513620349;mean squared error:0.0034079439642805773
degree:13;train score:0.9933429099055534;mean squared error:0.0032928617862816533
degree:15;train score:0.9933582413606227;mean squared error:0.0032852782382435095
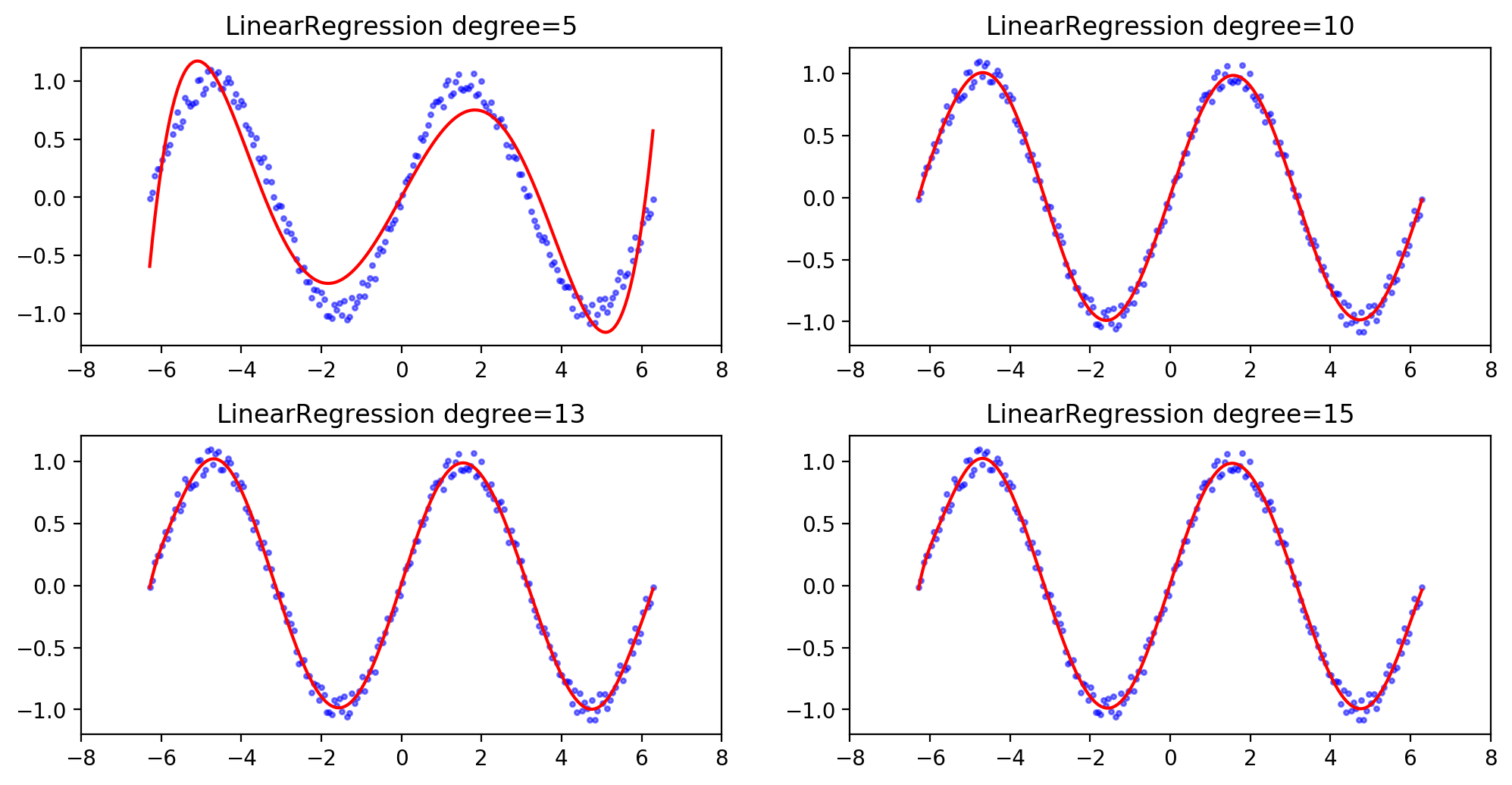
从上我们可以看到，在degree超过10之后，模型的score依旧在上涨，虽然上涨的幅度很小，但是确是实实在在的在上升的。因此我得到以下结论，在线性回归算法拟合正弦函数这个示例中，多项式的阶数越大其模型的score也会不断上升。只是后面的涨幅力度趋于平滑，而且貌似没有过拟合的状态。
本人尚在学习阶段，得到的结论皆属个人意见。如有错误，望请指出。
下面贴出5，10，13，15的拟合曲线图。
在这里插入图片描述

sklearn机器学习（四）线性回归算法拟合正弦函数

猜你喜欢