参考B站视频新手狂喜！目前B站最全最清晰的【机器学习算法】教程，从零开始详细解读，原理+代码实现，通通都在这里了！收藏慢慢学！！决策树/随机森林/聚类分析/人工智能_哔哩哔哩_bilibili
线性回归
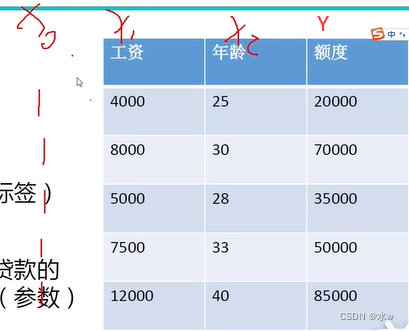
eg：银行贷款
- 数据：工资和年龄（特征，2个：x1,x2）
- 目标：预测银行会贷款给我多少钱（标签,Y）
- 考虑：工资和年龄都会影响最终银行贷款的结果，那么它们各自有多大的影响？（参数）
（1）可以列一个回归方程：
。整个方程只有参数不知道，那么方程的核心目标就是求出一个参数是最合适的？这就是我们要求解的目标。
通俗解释：x1,x2就是我们的两个特征（年龄和工资），Y就是银行最终会借给我们多少钱。我们现在要找的最合适的一条线（想象一个高维）来可以最好地拟合我们的数据点。
（2）那么现在，我们要怎么描述最拟合、最满足 这样的情况呢？我们假设：θ1是年龄的参数，θ2是工资的参数。
其中θ0是偏置项，θ1和θ2是权重项。当θ0改变时，平面会进行上下的浮动，就相当于把预测结果又进行了一个微调。核心的影响是θ1和θ2，微调是θ0。
我们在前面再添加一列X0都为1（补位，为了便于计算），那么拟合的平面就变成了下面这样：
（3）对于每一个样本(x1,x2)来说，其真值与方程计算出来的预测值之间存在的差距就是所谓的“误差”，因为此时真值与方程计算出来的预测值的X1和X2都是一样的。
不同样本的误差是不同的。
我希望我的误差项越小越好，并且接近于0才是一个完美的。通常损失函数就是这么定义的。损失函数等于0的时候，代表做到了一个极限。损失函数越接近0，代表者这件事情做得越好。这个就是机器学习当中无论什么样的损失函数，基本来说都是这样的一个出发点。
另外，
（4）求解时，把式子中与误差项相关的转换成与θ项相关的，做了一个代替之后就变成了最下面的式子。
通俗解释：要找一个θ，跟X组合之后，我希望它跟真实值越接近越好，也就是θ跟X组合之后能成为Y真实值的可能性应该越大越好。
（5）其中涉及到了似然函数：
参数跟数据是相关的，数据能验证这组参数。说白了似然函数描述了这样一件事：
什么样的参数跟我们的数据组合完之后，恰好是真实值
- i从1到m：我们是希望通过大量的数据去找到最合适的一个参数，相当于我们要做这样一个估计：希望用的数据越多，结果应该更准确一些。
- 累乘：独立同分布的前提下时，联合概率密度等于边缘概率密度的乘积
（6）为了似然函数中的累乘更好求解一些，我们在式子的两边取对数，将累乘转化为累加，就得到了一个对数似然
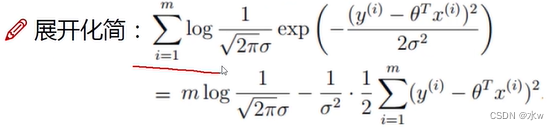
那么就要使
后面这部分越小，才能让式子的整体结果越大越好，即成为Y真实值的可能性越大。
常数项不用管，就变成了
这样一个目标函数，此时的目标函数当然是越小越好。我们要求什么样的θ，在此时能够使得整体的式子越小越好。这个式子还有一个通俗的叫法，叫最小二乘法。
（7）整个目标函数的求解过程：
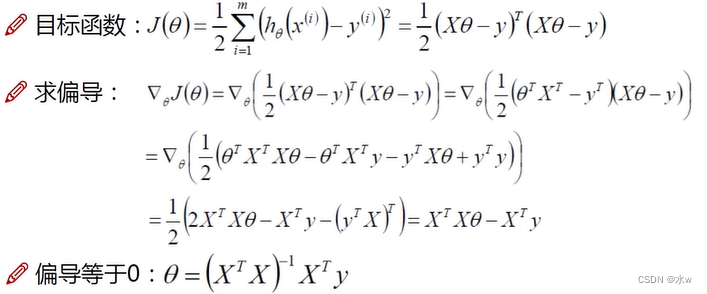
解释：
1、
此时的目标函数中的 X，是第几列特征，不能把它当成一个数，要当成一个矩阵。θ也是要当成一个矩阵。我们的目标是什么样的θ，能使得当前式子整个的J(θ)越小越好。
2、用J(θ)对θ求偏导。
3、让偏导=0，
， 即
，那么我们求出来的θ就是当前的一个极值点。
（8）另外，我们注意到这样的一个求解过程，对于机器学习来说，并没有一个学习的过程。那么学习的过程一个长什么样子？
感觉应该是机器先看到第一个样本（x1,x2），它得到一个结果，看和真实值之间做的怎么样。差了一些，那就需要调一调。再看下一个样本。这样重复进行。应该有一个渐进的过程。
还有求逆：
很多条件下，不可逆时，一旦矩阵是不可逆的时候，我的X，或者θ，就没办法求解了。
那么就引入了梯度下降，
- 引入：当我们得到了一个目标函数之后，如何进行求解？直接求解？（并不一定可解，线性回归可以当做是一个特例）。
- 常规套路：机器学习的套路就是我交给机器一堆数据，然后告诉它什么样的学习方式是对的（目标函数），然后让它去朝着这个方向去做。
当我们沿着梯度的反方向走时，是最快下山的方法。因此就叫梯度下降法。
每走一步（可以走大一点，也可以走小一点。通常情况下应该是小范围慢慢移动），重新计算梯度（可能方向会改变）。
- 如何优化：一口吃不成大胖子，我们要静悄悄地一步一步完成迭代（每次优化一点点，累积起来就是个大工程了）。
我们现在需要优化方程，找到最优的θ0和θ1。当我在找这些最优值的过程中，既要找θ0，也要找θ1，此时应该是分别找θ0和θ1，而不是一起找。因为数据样本之间是独立的，θ0对应X0，θ1对应X1，因此θ0和θ1之间也没有关系。
在图中，θ0表示一个轴，θ1也表示一个轴。我们先找的θ0最合适的一个方向，再找θ1最合适的一个方向，它俩一起前进，最终找到一个综合的方向。
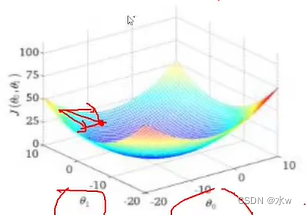
那么我们现在，
- 目标函数
- 寻找山谷的最低点，也就是我们的目标函数终点（什么样的参数能使得目标函数达到极值点）
- 下山分几步走？（更新参数）1、找到当前最合适的方向。2、走那么一小步，走快了该“跌倒”了。3、按照方向与步伐去更新我们的参数。
（9）我们将目标函数变为下面这样，
m：是为了建立的模型，在评估过程当中，尽可能多的满足样本。
加平方项：是为了使结果的差异更大一些。
除以m：相当于计算的是平均值。
其中
表示沿着梯度的反方向
走了一步，得到了一个新的θj，也就是完成了参数的更新。
注意：批量是求的所有样本的一个平均的最优的方向。但是一旦样本多了之后，做起来就非常慢。
注意：每次只找一个样本，虽然快但是不一定合适，有离群点或者噪音点，数据每一次朝着一个方向不一定都是朝着一个收敛方向，也不一定都是朝着一个好的方向，不太可控。
a：表示学习率（步长），对结果会产生巨大的影响，一般小一些。
如何选择：从小的时候，不行再小
每次更新只选择一小部分数据来计算，实用！！！数据样本数量选的大时，说明数据样本越多，当前希望这个结果越精确越好，但是速度会变慢。
