机器学习-线性回归的推导过程

表面理解的线性

对于给定的一组输入值x和输出值y，我们假定其关系为线性的，就会得出：
y = kx+b，即我们在大学前接触到的最基本的线性方程，只要我们求出k和b来，就可以求出整条直线上的点，这就是很多人认为的线性：

简单来说很多人认为：
线性回归模型假设输入数据和预测结果遵循一条直线的关系

但是，这种理解是一叶障目。

线性的含义

线性回归模型是：利用线性函数对一个或多个自变量 （x 或 (x1,x2,…xk)）和因变量（y）之间的关系进行拟合的模型。

也就是说，线性回归模型构建成功后，这个模型表现为线性函数的形式。

线性函数的定义是：一阶（或更低阶）多项式，或零多项式。

当线性函数只有一个自变量时，y = f(x)。
f(x) 的函数形式是：

f(x) = a + bx （a、b 为常数，且 b≠0）—— 一阶多项式
或者 f(x) = c (c 为常数，且 c≠0) —— 零阶多项式
或者 f(x) = 0 —— 零多项式

但如果有多个独立自变量，y=f(x1,x2,…,xk) 的函数形式则是：

f(x1,x2,…,xk)=a+b1x1+b2x2+…+bkxk
也就是说，只有当训练数据集的特征是一维的时候，线性回归模型可以在直角坐标系中展示，其形式是一条直线。

换言之，直角坐标系中，除了平行于 y 轴的那些直线之外，所有的直线都可以对应一个一维特征（自变量）的线性回归模型(一元多项式函数)。

但如果样本特征本身是多维的，则最终的线性模型函数是一个多维空间内的[一阶|零阶|零]多项式。

总结一下：特征是一维的，线性模型在二维空间构成一条直线；特征是二维的，线性模型在三维空间中构成一个平面；若特征是三维的，则最终模型在四维空间中构成一个体，以此类推。

线性回归的推倒

拟合

举个例子，我们的一个系统里边有两个特征值（x1和x2），这两个特征值共同决定了一个标签（y），而我们需要采用线性回归的方法去推倒x1和x2对于y的影响程度（参数）。
此时假设θ1是x1的参数，θ2是x2的参数，则有：

这个式子是代表了一个点，如果将所有的点都带入其中，就会在一个三维空间中描出所有的店，进而绘制出一个拟合平面，如下图：

将上述的式子整合为简短的表达方法为：

其中n为特征值的个数

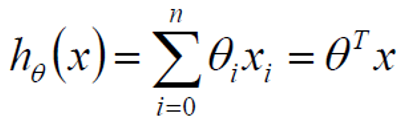
误差

众所周知，当我们吧数据进行拟合后，不可能所有的数据均落在拟合线或者拟合平面内，因此拟合值跟实际值之间肯定会产生一个误差（我们用ε来表示误差），因此对于每个样本点来说：

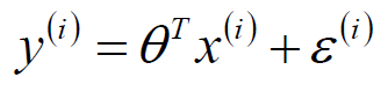
一般来说误差具有独立同分布的特点，并且符合正态分布，其均值为0，方差为θ的平方：

由于误差服从正态分布：

我们将误差函数与正态分布的公式组合（其中μ为0 ）：

将误差公式代入上述式子中：

在这里我们引入似然函数，似然函数在统计学中扮演着重要的角色，我们可以简单理解为什么样的参数跟我们的数据组合后恰好是真实值：

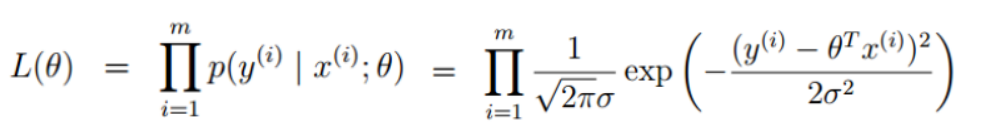
因为这个函数是一个累乘的式子，为了方便计算，我们将其取对数，将乘法变成加法，即为对数似然：

将式子展开化简：

根据概率和统计中所学的知识，我们知道，对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。 化简后减数和被减数均为正数，要使函数获得最大值，那么我们就要使减数越小越好：

此时我们要求的就是J(θ)的极小值：

因为这个函数本质上来说是一个面，因此它的极值一般会出现在偏导为0的地方，于是我们对J(θ)分别对x和y求偏导：

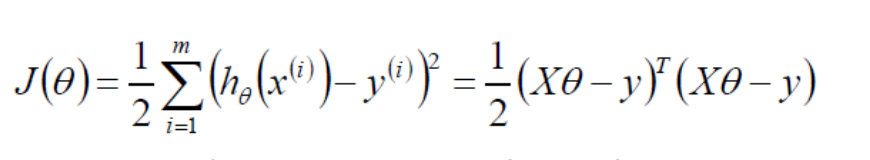
如果偏导为0，则：

评估方法

我们最常用的评估方法为：

其取值越接近于1，我们认为模型的拟合程度越好。