LLIS寒假学习(4)：动手学深度学习(pytorch版)：softmax回归解读

对比线性回归模型其输出为连续值，softmax回归模型的输出则为离散值。
对于像图像类别这样的离散值预测问题，我们可以使用诸如softmax回归在内的分类模型。

一.具体问题

考虑一个简单的图像分类问题，其输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为 $x_1$ ， $x_2$ ， $x_3$ ， $x_4$ 。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以用4像素表示出这3种动物），这些标签分别对应离散值 $y_1$ ， $y_2$ ， $y_3$ 。我们通常使用离散的数值来表示类别，例如 $y_1=1$ ， $y_2=2$ ， $y_3=3$ 。如此，一张图像的标签为1、2和3这3个数值中的一个。虽然我们仍然可以使用回归模型来进行建模，并将预测值就近定点化到1、2和3这3个离散值之一，但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。

二.softmax回归模型

softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别，所以权重包含12个标量（带下标的 $w$ ）、偏差包含3个标量（带下标的 $b$ ），且对每个输入计算 $o_1$ ， $o_2$ ， $o_3$ 这3个输出：
$o_1=x_1w_{11}+x_2w_{21}+x_3w_{31}+x_4w_{41}+b_1$ ，
$o_2=x_1w_{12}+x_2w_{22}+x_3w_{32}+x_4w_{42}+b_2$ ，
$o_3=x_1w_{13}+x_2w_{23}+x_3w_{33}+x_4w_{43}+b_3$ ，
既然分类问题需要得到离散的预测输出，一个简单的办法是将输出值 $o_i$ 当作预测类别是 $i$ 的置信度，并将值最大的输出所对应的类作为预测输出，即输出 $arg_imaxo_i$ ，例如，如果 $o_1$ ， $o_2$ ， $o_3$ 分别为0.1，10，0.1，由于 $o_2$ 最大，那么预测类别为2，其代表猫。
此时出现两个问题：

输出值的范围不确定。
由于输出值不确定，以及真实标签是离散值，因此不好衡量预测误差。

**softmax运算符（softmax operator）**解决了以上两个问题。
通过数学运算，将输出值变换成正值且和为1的概率分布：
在这里插入图片描述
其中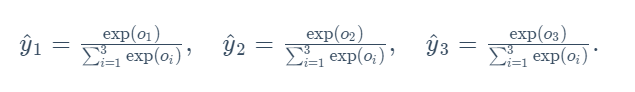
很明显，经过对数处理后，输出值全为正值且 $\hat{y}_1+\hat{y}_2+\hat{y}_3=1$ 。这时候，如果 $\hat{y}_2=0.8$ ，不管 $\hat{y}_1$ 和 $\hat{y}_3$ 的值是多少，我们都知道图像类别为猫的概率是80%。

三.矢量计算表达式

根据回归模型的定义，我们可以将上文提到的 $o_1$ ， $o_2$ ， $o_3$ 的表达式一并写成矢量的形式进行计算。
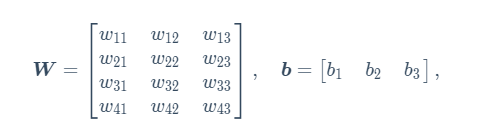
在这里插入图片描述
设高和宽分别为2个像素样本的特征为

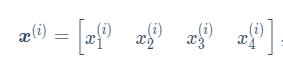
输出层的输出为

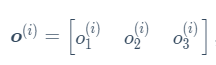
预测为狗、猫或鸡的概率为

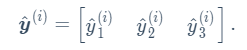
总的softmax回归计算表达式

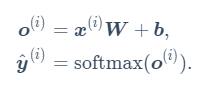
补充概念：
神经网络图：
在深度学习中，我们可以使用神经网络图直观地表现模型结构。下图使用神经网络图表示softmax回归模型。神经网络图隐去了模型参数权重和偏差。
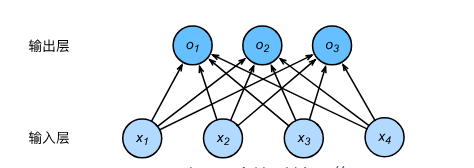
在这里插入图片描述
在所示的神经网络中，输入分别为 $x_1$ , $x_2$ , $x_3$ , $x_4$ ,因此输入层的输入个数为4。输入个数也叫特征数或特征向量维度。同理，该输出层的输出个数为3。
由于输出层的计算依赖全部的输入，也就是说，输出层中的神经元和输入层中各个输入完全连接。因此，这里的输出层又叫全连接层（fully-connected layer）或稠密层（dense layer）。

四.交叉熵损失函数

在上述图像分类的例子里，如果其中一个预测值比其他两个预测值大，那么就可以说明问题了。在衡量误差的时候，平方损失对于分类问题就显得过于严格，例如， $\hat{y}_1=\hat{y}_2=0.2$ 比 $\hat{y}_1=0$ , $\hat{y}_2=0.4$ 的损失要小很多，虽然两者都有同样正确的分类预测结果 $\hat{y}_3$ .
引入概念：交叉熵（cross entropy）

原文解释：
在这里插入图片描述
推荐博客：一文搞懂交叉熵在机器学习中的使用

交叉熵损失函数：
在这里插入图片描述