机器学习---决策树笔记

本帖为学习笔记帖，参照b站解读西瓜书、haoyutiangang以及课堂的内容来记的，如有漏错，欢迎批评指正。

在了解决策树之前，一些概念需要知道：

Question1：什么是信息熵？

熵：对一种事物的不确定性叫做熵，或者说混乱程度。

信息：

消除不确定性的事物
调整概率
排除干扰
确定情况

噪音：不能消除不确定性的事物

数据=信息+噪音

信息熵（information entropy）：是度量样本集合纯度最常用的一种指标。

Question2：熵如何量化？

参照一个不确定的事件作为单位：如抛硬币，我的不确定性相当于抛几次硬币的不确定性。如果是一枚硬币，50%正，50%反，就相当于一次抛硬币的不确定性，记为1bit。2枚硬币就是4种结果，3枚8种，以此类推，因此，抛硬币的次数与结果不确定性成指数关系。

概率均匀分布的情况：
有m种不确定情况，此时的需要抛 $n=\log_2^m$ 枚硬币，那么此时的熵就是 $n$ bit。

每种情况概率不相等情况:

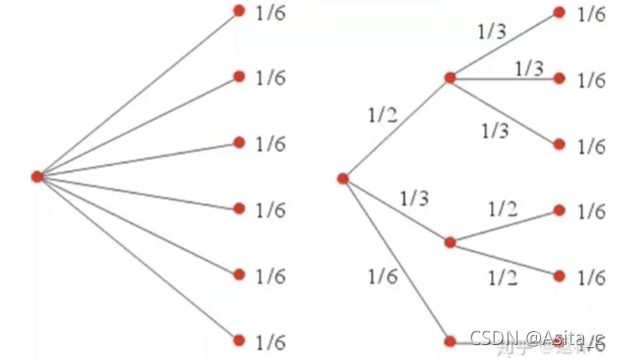
在这里插入图片描述
此时有三种情况，分布p分别为：1/2、1/3、1/6，我们这三种情况分别都拆成概率为1/6的情况，就近似转换成了左图的等概率情况，但实际上不是等概率，因此，我们就可以借助等概率情况来计算不等概率情况。
当分布为1/2时，此时需要的硬币为： $log_2^6-\log_2^3$ (因为后面三种其实是一种情况)，同理，分布为1/3为： $log_2^6-\log_2^2$ ，分布为1/6为： $log_2^6-\log_2^1$ ，因此左图总的需要硬币个数为（熵）： $\frac{1}{2}(\log_2^6-\log_2^3)+\frac{1}{3}(\log_2^6-\log_2^2)+\frac{1}{6}(\log_2^6-\log_2^1)=\frac{1}{2}\log_2^{(2/1)}+\frac{1}{3}\log_2^{(3/1)}+\frac{1}{6}\log_2^{(3/1)}$

因此，信息熵( $D$ )公式为：
$\mathbf{Ent}(D)=-\sum_{k=1}^{ \vert \mathcal{Y} \vert}p_k\log_2^{p_k}$

$\mathbf{Ent}(D)$ 越小，则 $D$ 的纯度越高。

信息如何量化：

例：小明不知道选择题（等概率事件）是ABCD哪个选项正确时的熵： $log_2^4=2$
告诉小明C有一半概率是正确的，小明知道C有一般概率后的不确定性（熵）： $\frac{1}{6}\log_2^6+\frac{1}{6}\log_2^6+\frac{1}{2}\log_2^2+\frac{1}{6}\log_2^6=1.79$ ，因此，告诉小明C有一半概率是正确的相当于提供的信息为： $2 - 1.79 = 0.21$

信息增益(ID3)：

西瓜书上的定义是这样的：
假定离散属性 $a$ 有 $V$ 个可能的取值 ${a^1,a^2,...,a^V\}$ ，若使用 $a$ 来对样本集 $D$ 进行划分，则会产生 $V$ 个分支结点，其中，第 $v$ 个分支结点包含了 $D$ 中所有在属性 $a$ 上的取值为 $a^v$ 的样本，记为 $D^v$ 。我们根据信息熵的公式，再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重 $\vert D^v \vert / \vert D \vert$ ，即样本数越多的分支结点的影响越大，于是可计算出属性 $a$ 对样本集 $D$ 的“信息增益”（information gain）
$\mathbf{Gain}(D,a)=\mathbf{Ent}(D)-\sum_{v=1}^V\frac{\vert D^v \vert}{\vert D\vert}\mathbf{Ent}(D^v)$

**注：**这里由引出了一个概念：条件熵

条件熵

条件熵 $H(Y\vert X)$ 表示在已知随机变量 $X$ 的条件下随机变量 $Y$ 的不确定性。记为随机变量 $X$ 给定条件下的随机变量 $Y$ 的条件熵 $H(Y\vert X)$

推导：
$\begin{aligned} H(Y\vert X) &=\sum_{x \in X}p(x)H(Y\vert X=x)\\ &=-\sum_{x \in X}p(x)\sum_{y \in Y}p(y \vert x)\log p(y\vert x)\\ &=-\sum_{x\in X}\sum_{y\in Y}p(x,y)\log p(y\vert x) \end{aligned}$
其中 $H (X)$ 表示的是信息熵 $\iff$ $\mathbf{Ent}(D)$ (一个意思不同描述)；
所以：条件熵也可以写成：
$\sum_{v=1}^V\frac{\vert D^v \vert}{\vert D\vert}\mathbf{Ent}(D^v)$

所以：信息增益=信息熵-条件熵

以一个具体的例子来计算信息增益，具体详情在西瓜书 $P_{75}$ ~ $P_{77}$ 页
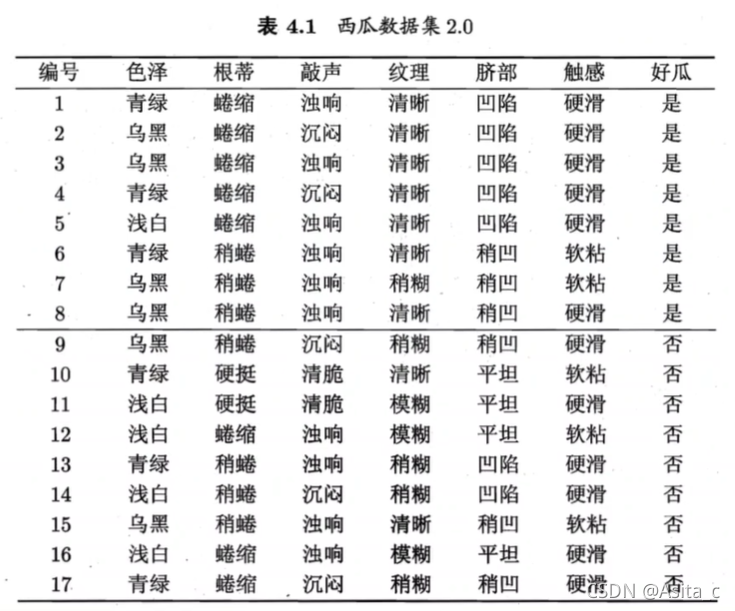
在这里插入图片描述
正例 $p_1=\frac{8}{17}$ ，反例 $p_2=\frac{9}{17}$

根结点的信息熵为：
$\begin{aligned} \mathbf{Ent}(D)&=-\sum_{k=1}^2p_k\log_2^{P_k}\\ &=-\left( \frac{8}{17}\log_2^{\frac{8}{17}} +\frac{9}{17}\log_2^{\frac{9}{17}}\right)\\ &=0.998 \end{aligned}$

以色泽为例，计算色泽的信息增益：
色泽有3种：青绿、乌黑、浅白，三种颜色的子集分别记为 $D^1,D^2,D^3$
三个分支结点的信息熵为：
$\mathbf{Ent}(D^1)=-\left( \frac{3}{6}\log_2{\frac{3}{6}}+\frac{3}{6}\log_2{\frac{3}{6}} \right)=1.000$
$\mathbf{Ent}(D^2)=-\left( \frac{4}{6}\log_2{\frac{4}{6}}+\frac{2}{6}\log_2{\frac{2}{6}} \right)=0.918$
$\mathbf{Ent}(D^3)=-\left( \frac{1}{5}\log_2{\frac{1}{5}}+\frac{4}{5}\log_2{\frac{4}{5}} \right)=0.722$

属性“色泽”的信息增益为：
$\begin{aligned} \mathbf{Gain}(D,色泽)&=\mathbf{Ent}(D)-\sum_{v=1}^3 \frac{\vert D^v \vert}{\vert D \vert}\mathbf{Ent}(D^v)\\ &=0.998-\left( \frac{6}{17}*1.000+\frac{6}{17}*0.918+\frac{5}{17}*0.722 \right)\\ &=0.109 \end{aligned}$
同理，其他属性的信息增益为：
$\mathbf{Gain}(D,根蒂)=0.143；\mathbf{Gain}(D,敲声)=0.141；$
$\mathbf{Gain}(D,纹理)=0.318；\mathbf{Gain}(D,脐部)=0.289；$
$\mathbf{Gain}(D,触感)=0.006；$
属性“纹理”的信息增益最大，因此作为第一层的划分属性，然后根据纹理属性的三个取值的基础上，继续求信息增益，一直下去得到的决策树为：
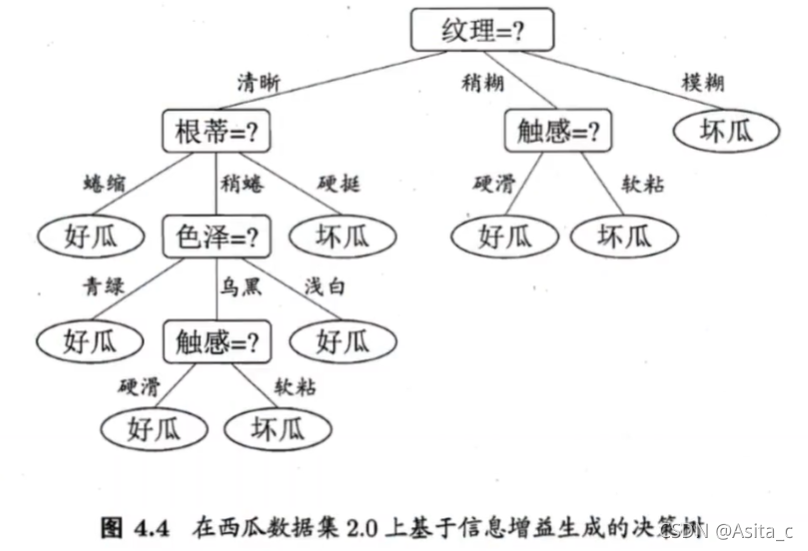
在这里插入图片描述

信息增益率( $\mathbf{C4.5}$ )

由于信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，著名的 $\mathbf{C4.5}$ 决策树算法不直接使用信息增益，而是使用“增益率”来选择最优划分属性，增益率定义为：
$\mathbf{Gain}\_\mathbf{ratio}(D,a)=\frac{\mathbf{Gain}(D,a)}{\mathbf{IV}(a)}$

其中， $\mathbf{IV}(a)=-\sum_{v=1}^V\frac{\vert D^V \vert}{\vert D \vert}\log_2^{\frac{\vert D^v \vert}{\vert D \vert}}$ ， $\mathbf{IV}(a)$ 表示属性 $a$ 的固有值，属性 $a$ 的可能取值数目越多（即 $V$ 越大），则 $\mathbf{IV}(a)$ 的通常值越大，所以信息增益率可以起到“惩罚”个数多的属性的目的。

使用方法： $[\mathbf{Quinlan,1993}]$ ：先从候选划分属性中找出信息增益高于平均水平的属性，再从中选取增益率高的。

基尼指数

$\mathbf{CART}$ 决策树 $[\mathbf{Breiman \ et \ al., \ 1984}]$ 使用“基尼系数”（ $\mathbf{Gini \ index}$ ）来选择划分属性。数据集“ $D$ ” 的纯度可用基尼值来度量：
$\begin{aligned} \mathbf{Gini}(D)&=\sum_{k=1}^{\vert \mathcal{Y} \vert} \sum_{k^{,} \neq k}p_kp_{k^,}\\ &=1-\sum_{k=1}^{\mathcal{Y}}p_k^2 \end{aligned}$
$\mathbf{Gini}(D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一样的概率，即 $\mathbf{Gini}(D)$ 越小，数据集 $D$ 纯度越高。

属性 $a$ 的基尼指数定义为：
$\mathbf{Gini\_index}(D,a)=\sum_{v=1}^{V}\frac{\vert D^v \vert}{\vert D \vert}\mathbf{Gini}(D^v)$

因此，在候选集合 $A$ 中应该选择使得划分后基尼系数最小的属性作为最优划分属性，即：
$a_*=\argmin_{a \in A}\mathbf{Gini\_index}(D,a)$

以下是三种基本算法的决策树的区别

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝	特征属性多次使用
ID3	分类	多叉树	信息增益	不支持	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益率	支持	支持	支持	不支持
CART	分类回归	二叉树	基尼指数均方差	支持	支持	支持	支持

划分标准的差异：ID3 使用信息增益偏向特征值多的特征，C4.5 使用信息增益率克服信息增益的缺点，偏向于特征值小的特征，CART 使用基尼指数克服C4.5 需要求log 的巨大计算量，偏向于特征值较多的特征。
使用场景的差异：ID3 和C4.5 都只能用于分类问题，CART 可以用于分类和回归问题；ID3 和C4.5 是多叉树，速度较慢，CART 是二叉树，计算速度很快；
样本数据的差异：ID3 只能处理离散数据且缺失值敏感，C4.5 和CART 可以处理连续性数据且有多种方式处理缺失值；从样本量考虑的话，小样本建议C4.5、大样本建议CART。C4.5 处理过程中需对数据集进行多次扫描排序，处理成本耗时较高，而CART 本身是一种大样本的统计方法，小样本处理下泛化误差较大；
样本特征的差异：ID3 和C4.5 层级之间只使用一次特征，CART 可多次重复使用特征； •剪枝策略的差异：ID3 没有剪枝策略，C4.5 是通过悲观剪枝策略来修正树的准确性，而CART 是通过代价复杂度剪枝。