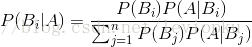【AI数学原理】概率机器学习（二）：朴素贝叶斯分类器

朴素贝叶斯分类器，英文叫’naive Bayes classifier’.顾名思义，就是很naive的一个算法。naive主要体现在一个方面 —— “属性条件独立性假设”。就是用贝叶斯算法进行分类的时候，假设所有的属性相互独立。
公式符号说明：

$A$ 表示输入属性，等价x和 $\vec{x}$ (x粗写表示这是一个多维向量)。
$B_i$ 表示分类的类别，等价 $c$ 。
$x_i$ 表示x的一个维度（属性）

1 . 预备知识

贝叶斯公式（不熟悉可参考上一篇博文：【AI数学原理】概率机器学习（一）：从贝叶斯公式开始）
贝叶斯分类原理（在下面给出解释）：
首先贝叶斯分类器具有所有分类器一样的功能：根据输入属性给出一个分类结果
比如男友质量分类器，输入属性x：
x是一个多维向量，包含:

{颜值，才艺，厨艺，脾气，对异性博爱，人品}
等6个维度。
输出的分类结构为，的取值范围是：
{优质，一般，渣男，好人卡}
        在这里我们对每个属性进行0-1编码量化（每个属性取值都在0和1之间，越大说明程度越高）。比如，输入属性x={颜值=0.5，才艺=0.3，厨艺=0，脾气=1，对异性博爱程度=0.9}，那么输出极可能为‘渣男’。但’渣男’并不是绝对答案，因为每个女生都有一套评分标准。女生的心理就是我们分类器所处的环境，我们对环境是不可知的。但是我们非要对这个男友进行分类，做法如下：我们在微博上看大量相关的新闻，看看大家的分类标准，等心里大概对大多数女生的价值观有一个把握后，再对这个男生进行分类，这样的分类结果才是比较准确的。大部分女生认为的那个类别便是最后的分类结果，这就是贝叶斯分类器的原理。（在这里扯个题外话：当年帝吧经常有颜值评分的帖子，看多了这样的贴子，大家的评分标准慢慢接近那个所谓的‘标准值’，这个标准值就是分类器对分类目标的分类把握。）
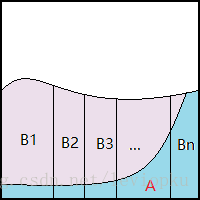
        那么，对广大女生心理标准的探索，就是贝叶斯分类器的所做的。如果认真看过上一篇博文的朋友，一定熟悉这张图：

这张图是我用来证明贝叶斯公式的：
那么，把实际问题映射到这张图上就是说：表示输入属性，表示分类结果。当输入是的时候，的可能实际类别是：，，…，。分类器只能选出一个类别作为输出结果，那么怎么选呢？当然要选可能性最大的那个分类咯：
在图上可以清晰看到， $A$ 与 $B_n$ 的相交面积最大，所以贝叶斯分类器会把 $A$ 分类到 $B_n$ 。
即：
输出类别= argmax(P(判断类别|输入属性))
公式 0
事实上，要进行更智能的分类，可以加一个风险加权值，通过最小化风险来求得分类结果（这里只讨论思维，详细可以下一篇博文再讨论）。
        接着上面的例子，在以前的微博里，女生们可能把这种属性的男生分类成，，…，。但大部分妹子还是把他分类在，所以贝叶斯分类器的分类结果就是。
        写到这里，我才发现这个例子并不是很恰当。容易误导读者以为贝叶斯分类器是一个投票分类的算法。事实上不是这样。实际分类过程中，我们没办法找大量女生来投票，只能以往经验（微博）中总结得到先验概率 ( )和似然概率 ( | )，然后通过贝叶斯公式获得结果。怎么操作呢？
- 首先进行用数据对分类器进行训练，这里的训练无非就是对训练数据进行一些统计（都有哪些类别，每种类别的概率等），根据大数定律，当训练集包含充足的独立同分布样本时，先验概率 $P$ ( $B_i$ )可通过各类样本出现的频率来进行估计。
- 然后获取似然概率 $P$ ( $A$ | $B_i$ )，由于它涉及关于 $A$ 所有属性的联合概率，难以从有限的训练样本直接估计而得。那么就可以引出这篇博文的主角——“朴素贝叶斯分类器”了。

2 . 朴素贝叶斯分类器

如上面最后一句话所说，朴素贝叶斯分类器就是解决似然概率难以统计获得的问题。假设每个属性独立地对分类结果产生影响。
怎么理解上面这句话呢，属性之间不相互独立的例子如下：一个颜值=1，才华=1的男生有着1+1>2的效果，始于颜值，忠于才华就是这个意思。还比如说，才华高人品低的情况下，才华高反而起了反作用。
现在就是要naive地认为每个属性都是独立产生影响的。
则贝叶斯公式可以重写为：

P

$P$ (

c

$c$ | x) =

\frac{P (c) P (\vec{x} | c)}{P (\vec{x})}

$\frac{P(c)P(\vec{x}|c)} {P(\vec{x})}$ =

\frac{P (c)}{P (\vec{x})}

$\frac{P(c)} {P(\vec{x})}$

\prod_{i = 1}^{d}

$\prod_{i=1}^d$

P (x_{i} | c)

$P(x_i|c)$
( x =

\vec{x}

$\vec{x}$ )
公式 1
通过统计求单独的属性对结果的似然概率是很容易的，所有单独属性似然概率的乘积就是

P

$P$ (

A

$A$ |

B_{i}

$B_i$ )了。那么，上面公式里的

P

$P$ (

x_{i}

$x_i$ |

c

$c$ )怎么求呢？

对于离散情况

离散情况的意思是：各属性的取值是离散的，比如说颜值的取值直接就是{高，中，低}这样的离散值，而不是0.889这样的连续取值，对于离散情况直接统计出来就行了：

P (x_{i} | c) = D_{c, x i} / D_{c}

$P(x_i|c) = D_{c,xi} / D_c$

D_{c, x i}

$D_{c,xi}$ 表示

D_{c}

$D_c$ 中在第i个属性取值为

x_{i}

$x_i$ 的样本组成的集合，

D_{c}

$D_c$ 表示训练集

D

$D$ 中第

c

$c$ 类样本组成的集合。
最后的

P

$P$ ( x|

c

$c$ )就把各

P

$P$ (

x_{i}

$x_i$ |

c

$c$ )累乘起来就可以了，代入 公式1可以求得

P

$P$ (

c

$c$ | x)。

对于连续情况

当x各维度连续取值时，你不可能在训练的时候遍历所有的取值。怎么理解呢？当训练数据某个属性取值有{0.1, 0.2, 0.3, 0.4, … , 1}，当你用训练后的分类器去对新对象进行分类，而这个新对象在这个属性的取值是0.15，并不存在你的训练集中，这就是问题所在。那怎么解决呢？
我们有中心极限定理：

随机变量如果是有大量独立的而且均匀的随机变量相加而成，那么它的分布将近似于正态分布。

上面是引用百度百科，这是对中心极限定理的总结。这个定理怎么证明呢？自己去百度，这里不做讨论。。。。
我用白话再翻译一遍：
如果变量的取值满足独立（可以不同分布），那么这些变量叠加之后的分布是满足正态分布的。这也是自然界随处可见各种‘钟形’分布的原因。
在这里，我们也可以假设 $P$ ( $x_i$ | $c$ )服从正态分布，求得训练样本中 $P$ ( $x_i$ | $c$ )的期望和方差，对 $P$ ( $x_i$ | $c$ )的取值做一个正态分布建模，如下：
假定 $P$ ( $x_i$ | $c$ ) ~ $N$ ( $\mu$ , $\sigma^2$ )，其中 $\mu$ 和 $\sigma^2$ 分别是第c类样本在第i个属性上取值的均值和方差：

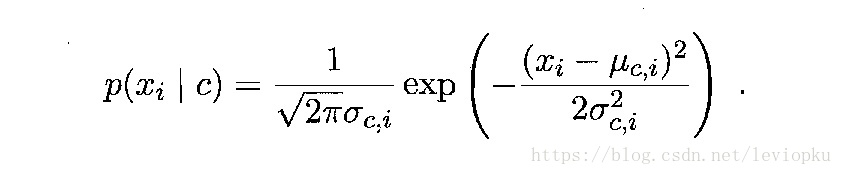
那这样就解决了连续取值问题，当输入属性取值xi并未在训练样本中出现，直接把这个取值输入

N

$N$ (

μ

$\mu$ ,

σ^{2}

$\sigma^2$ )中，获得的取值就是

P

$P$ (

x_{i}

$x_i$ |

c

$c$ )了。
同上，最后的p( x|c)就把各

P

$P$ (

x_{i}

$x_i$ |

c

$c$ )累乘起来就可以了，代入 公式1可以求得

P

$P$ (

c

$c$ | x)。

3. 总结

对于朴素贝叶斯分类器的操作可以理解如下：

输入大量训练样本，每个样本包括属性和类别，属性又有连续属性和离散属性之分。
对样本进行统计: 都有哪些类别，每种类别占比多少( $P$ ( $c$ ))，每个属性对样本分类单独造成的影响( $P$ ( $x_i$ | $c$ ))
对离散取值的属性可通过直接统计求得 $P$ ( $x_i$ | $c$ )；而对于连续取值的属性需要进行一个正态分布建模，求出训练样本中 $P$ ( $x_i$ | $c$ )的期望和方差，代入到 $N$ ( $\mu$ , $\sigma^2$ )中完成建模。
根据上述3个步骤，我们可以获得 $P$ ( $c$ )和各属性的 $P$ ( $x_i$ | $c$ )，那么直接代入公式1中，就可以求得 $P$ ( $c$ |x)了。
那最终进行分类，就比较各类别的 $P$ ( $c$ |x)（即取不同的c值），最大的那个就是我们的分类，即公式0所表示的。