前言:在正式讲述朴素贝叶斯分类器之前,先介绍清楚两个基本概念:判别学习方法(Discriminative Learning Algorithm)和生成学习方法(Generative Learning Algorithm)。
上篇博文我们使用Logistic回归解决二类分类问题,解决过程是在解空间中寻找一条直线(其实准确来说是曲线、曲面、超平面)直接把两个样本的类别区分开,作为决策边界。当我们有一个新的样本加入时,直接看它在边界的哪一侧便可。这种解决方法便是判别学习方法。而生成学习方法,则是分别对两个类别进行建模,当有新的样本加入时,我们可以看看这个样本对哪个模型匹配程度较高,便可判断它属于哪个类型。从数学上讲,就是计算这个新样本分别匹配两个模型的后验概率。更形式化来讲,判别学习方法是直接对P(y|x)进行建模或者直接学习输入空间到输出空间的映射关系,其中x是样本的特征向量,y是输出的分类类别,其本身不能反映训练数据本身的特性,反映的是异类数据之间的差异,直接面对预测,往往学习的准确率更高,简化学习问题。就好比我们区分绵羊和山羊的羊群时,给它们划一条边界;而生成学习方法则是先对P(x|y)(条件概率)和P(x)(先验概率)进行建模,然后按照贝叶斯公式计算P(y|x)。所以就可以从统计的角度表示数据的分布情况,能够反映同类数据本身的相似度,并且训练数据量较少时仍然适用。但它不关心到底划分各类的那个分类边界在哪。就好比我们区分山羊和绵羊时,先掌握它们各自的特征(有毛没毛,有角无角等),然后再进行区分(稍微想一下,如果出现一个羊羔,你很难简单地根据边界来判断它是属于绵羊或山羊,此时使用生成学习方法计算它分别属于绵羊和山羊的概率作出的决策可能会更加保险)。
常见的判别模型有:线性回归(包括局部线性)、Logistic回归、支持向量机、神经网络等。
常见的生成模型有:朴素贝叶斯模型、隐马尔科夫模型、高斯混合模型等。
一、问题引入
前言所述,本文所要介绍的算法是朴素贝叶斯分类器,分为输入的特征向量为连续和离散两种情况,属于生成模型,区别于Logistic回归的判别模型。实际上,Logistic回归有一个泛化(generalization)的模型:高斯判别模型(GDA),属于生成模型,它与Logistic回归的关系如图:
其中使用的类条件分布是多元高斯分布。
此外本文再介绍贝叶斯分类器的另一个最典型也是最常用的应用:垃圾邮件分类,此模型使用的类条件分布是多项式分布。这两种分类模型都基于贝叶斯公式,只是使用了不同的类条件分布,即条件概率的分布函数。
根据贝叶斯公式:
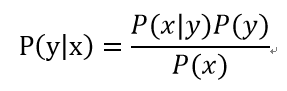
一般情况下,我们认为P(x)(先验概率)对于每个类别来说是一个常数,根据类别数而定,即
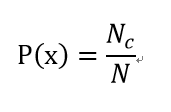
其中N是训练集的对象数目,Nc是属于C类的对象数量。P(y)是当前训练数据上y属于某一类的概率。这些变量都可以直接根据训练样本计算,不难求得。计算的重点和难点在于P(x|y),取决于它服从什么分布。
二、问题分析
我们首先分析基于高斯判别模型的贝叶斯分类器。
1.高斯判别模型
(1)在GDA中,假设P(x|y)服从多元高斯分布。多元高斯分布是高斯分布在多维变量下的扩展,它的参数是均值向量μ和协方差矩阵Σ,Σ是n阶对称正定矩阵。多元高斯分布的概率密度公式为:
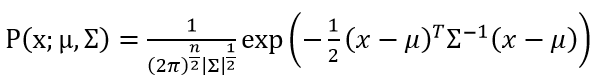
其中|Σ|是矩阵的行列式的值。协方差矩阵可以由协方差函数Cov求得,协方差函数的计算公式是:
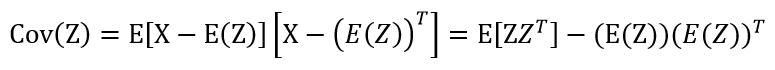
假定y有c个类别,即y∈{1, 2, … , c},那么条件概率服从以下公式:
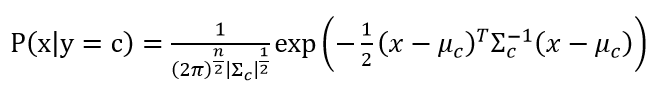
之后就是对均值向量μ和协方差矩阵∑进行参数估计了,仍然是使用最大似然估计,似然函数以及计算过程已经介绍过多次,下面直接给出结果:
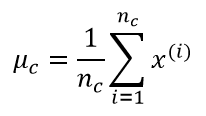
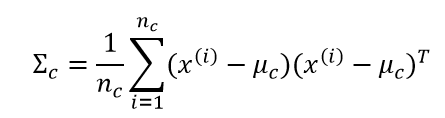
下面给出三类数据分类的Matlab代码实现。
(2)代码实现
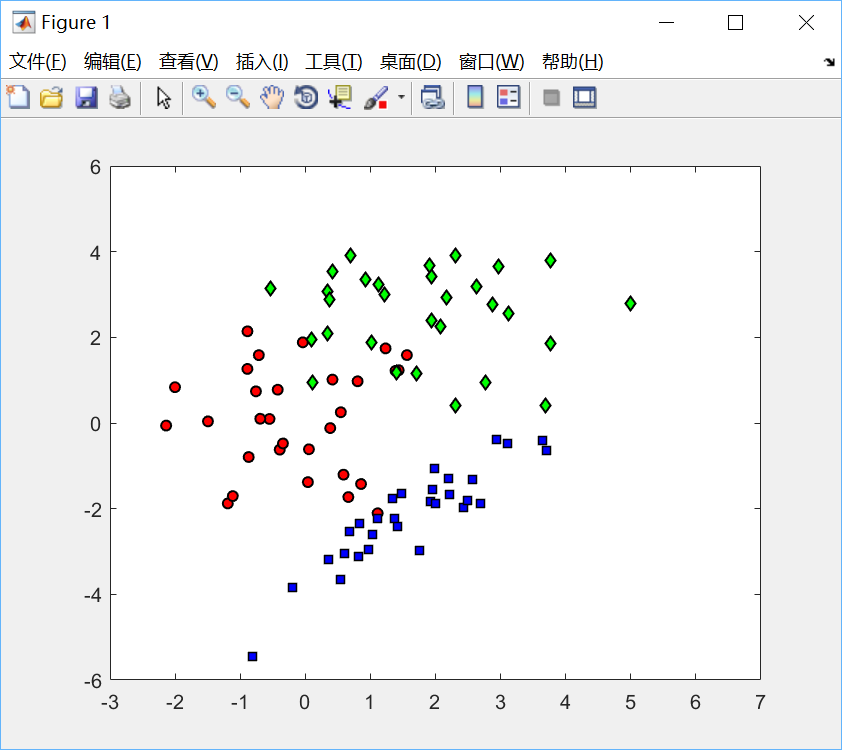
1)导入数据并绘制散点图
% 导入数据
load('bc_data')
% 绘制散点图
cl = unique(t); % 类别标签去重
col = {'ko','kd','ks'} % 指定散点形状
fcol = {[1 0 0],[0 1 0],[0 0 1]}; % 指定散点颜色
figure(1);
hold off
for c = 1:length(cl)
pos = find(t==cl(c)); % 分别查找类别1,2,3的元素位置下标
plot(X(pos,1),X(pos,2),col{c},... % 分别画出每种类别的散点图
'markersize',10,'linewidth',2,...
'markerfacecolor',fcol{c});
hold on
end
xlim([-3 7])
ylim([-6 6])
绘制效果如下:
2) 假设各类服从多元高斯分布
%% 计算各类的均值向量和协方差矩阵
class_var = [];
for c = 1:length(cl)
pos = find(t==cl(c));
class_mean(c,:) = mean(X(pos,:));
class_var(:,:,c) = cov(X(pos,:),1);
end
%% 绘制各类高斯分布图
figure(1);
hold off
[Xv,Yv] = meshgrid(-3:0.1:7,-6:0.1:6);
for c = 1:length(cl)
temp = [Xv(:)-class_mean(c,1) Yv(:)-class_mean(c,2)];
tempc = class_var(:,:,c);
const = -log(2*pi) - log(det(tempc));
Probs = exp(const - 0.5*diag(temp*inv(tempc)*temp'));% 多元高斯分布公式
contour(Xv,Yv,reshape(Probs,size(Xv)));% 绘制等概率线
end绘制效果如下:
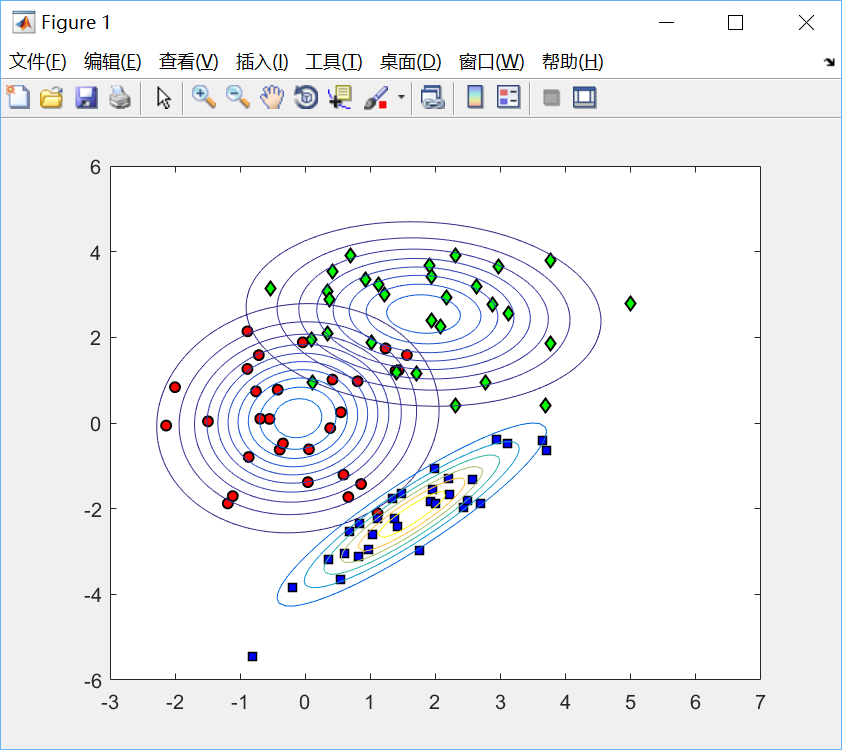
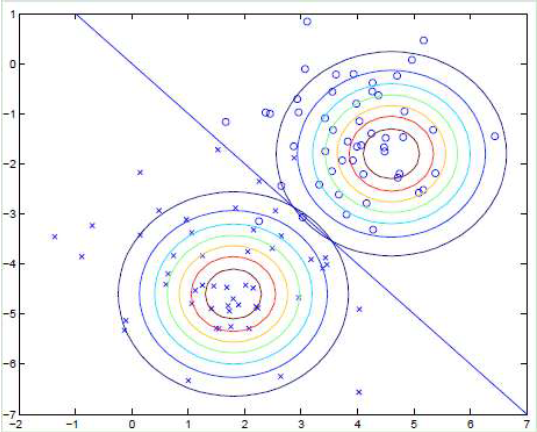
之后我们可以画出分类概率的等概率图,即具有决策概率的边界:
%% 计算样本预测分类概率
[Xv,Yv] = meshgrid(-3:0.1:7,-6:0.1:6);
Probs = [];
for c = 1:length(cl)
temp = [Xv(:)-class_mean(c,1) Yv(:)-class_mean(c,2)];
tempc = class_var(:,:,c);
const = -log(2*pi) - log(det(tempc));
Probs(:,:,c) = reshape(exp(const - 0.5*diag(temp*inv(tempc)*temp')),size(Xv));
end
Probs = Probs./repmat(sum(Probs,3),[1,1,3]); % 乘先验概率
%% 绘制分类概率的等概率线图
figure(1);hold off
for i = 1:3
subplot(1,3,i);
hold off
for c = 1:length(cl)
pos = find(t==cl(c));
plot(X(pos,1),X(pos,2),col{c},...
'MarkerSize',5,'LineWidth',1,...
'markerfacecolor',fcol{c});
hold on
end
xlim([-3 7])
ylim([-6 6])
contour(Xv,Yv,Probs(:,:,i));
ti = sprintf('class %g',i);
title(ti);
end绘制效果如下:
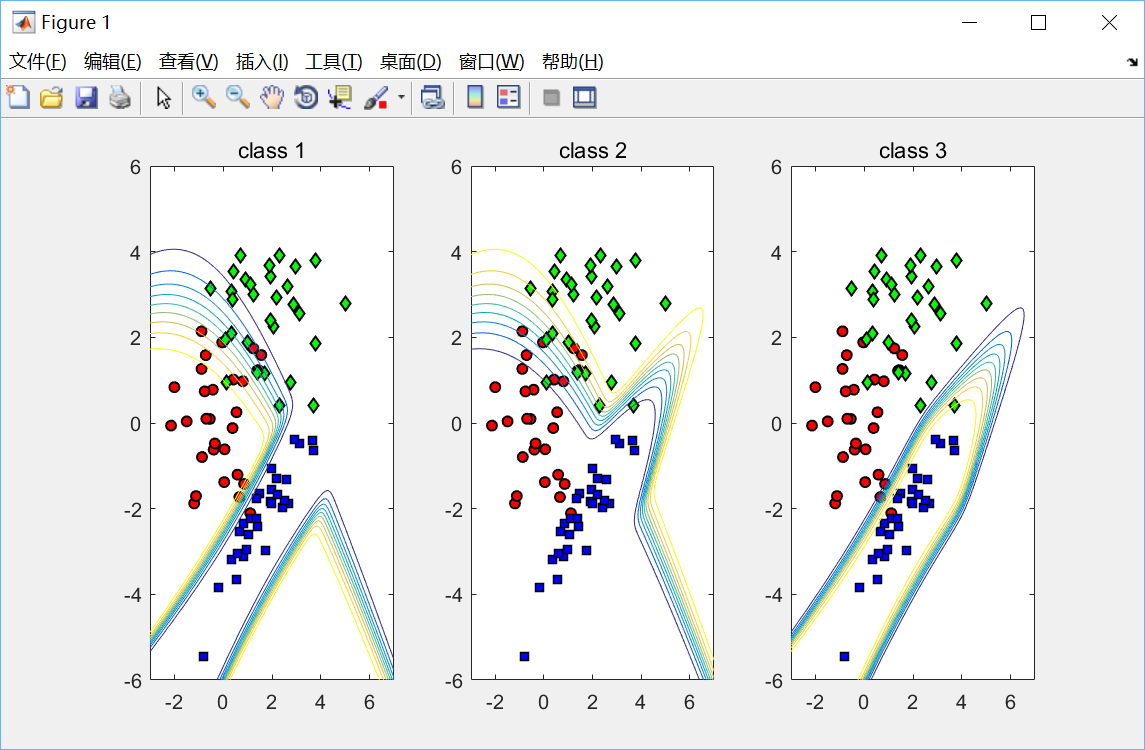
3)以上程序并未作出朴素(Naive)贝叶斯假设,即特征向量中各变量并不一定是两两相互独立的,所以参数量非常庞大,模型变得非常复杂,在一些简单问题中并无必要。因此可作出朴素贝叶斯假设:n维类条件分布能分解为n个单变量分布,此时每一维随机变量之间是相互独立,参数量大大减少,但此代价是模型灵活性降低。绘制朴素贝叶斯假设后的类条件分布的等概率线:
%% 计算各类的均值向量和协方差矩阵,并作出朴素贝叶斯假设
for c = 1:length(cl)
pos = find(t==cl(c));
% Find the means
class_mean(c,:) = mean(X(pos,:));
class_var(c,:) = var(X(pos,:),1);
end
%% 绘制各类的高斯分布图
[Xv,Yv] = meshgrid(-3:0.1:7,-6:0.1:6);
for c = 1:length(cl)
temp = [Xv(:)-class_mean(c,1) Yv(:)-class_mean(c,2)];
tempc = diag(class_var(c,:));
const = -log(2*pi) - log(det(tempc));
Probs = exp(const - 0.5*diag(temp*inv(tempc)*temp'));
contour(Xv,Yv,reshape(Probs,size(Xv)));
end
绘制效果如下:
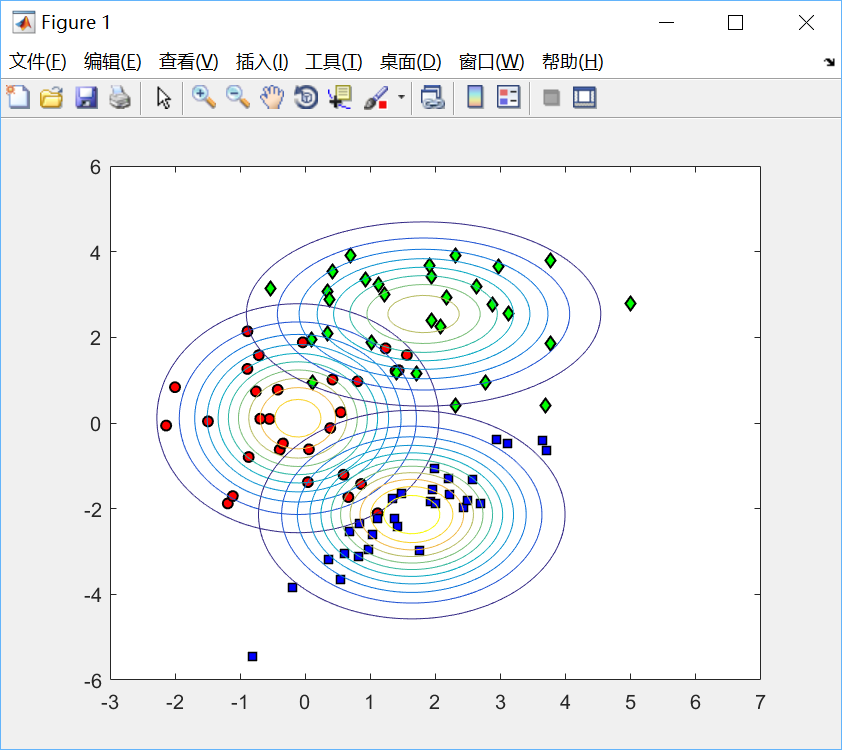
同样地,也可以继续绘制分类概率的等概率线图:
%% 计算样本预测分类概率
[Xv,Yv] = meshgrid(-3:0.1:7,-6:0.1:6);
Probs = [];
for c = 1:length(cl)
temp = [Xv(:) - class_mean(c,1) Yv(:) - class_mean(c,2)];
tempc = diag(class_var(c,:));
const = -log(2*pi) - log(det(tempc)); % 多元高斯分布
Probs(:,:,c) = reshape(exp(const - 0.5*diag(temp*inv(tempc)*temp')),size(Xv));
end
Probs = Probs./repmat(sum(Probs,3),[1,1,3]); % 乘先验概率
%% Plot the predictive contours
figure(1);hold off
for i = 1:3
subplot(1,3,i);
hold off
for c = 1:length(cl)
pos = find(t==cl(c));
plot(X(pos,1),X(pos,2),col{c},...
'markersize',5,'linewidth',1,...
'markerfacecolor',fcol{c});
hold on
end
xlim([-3 7])
ylim([-6 6])
contour(Xv,Yv,Probs(:,:,i)); % 等概率密度线
ti = sprintf('class %g',i);
title(ti);
end
绘制效果如下:
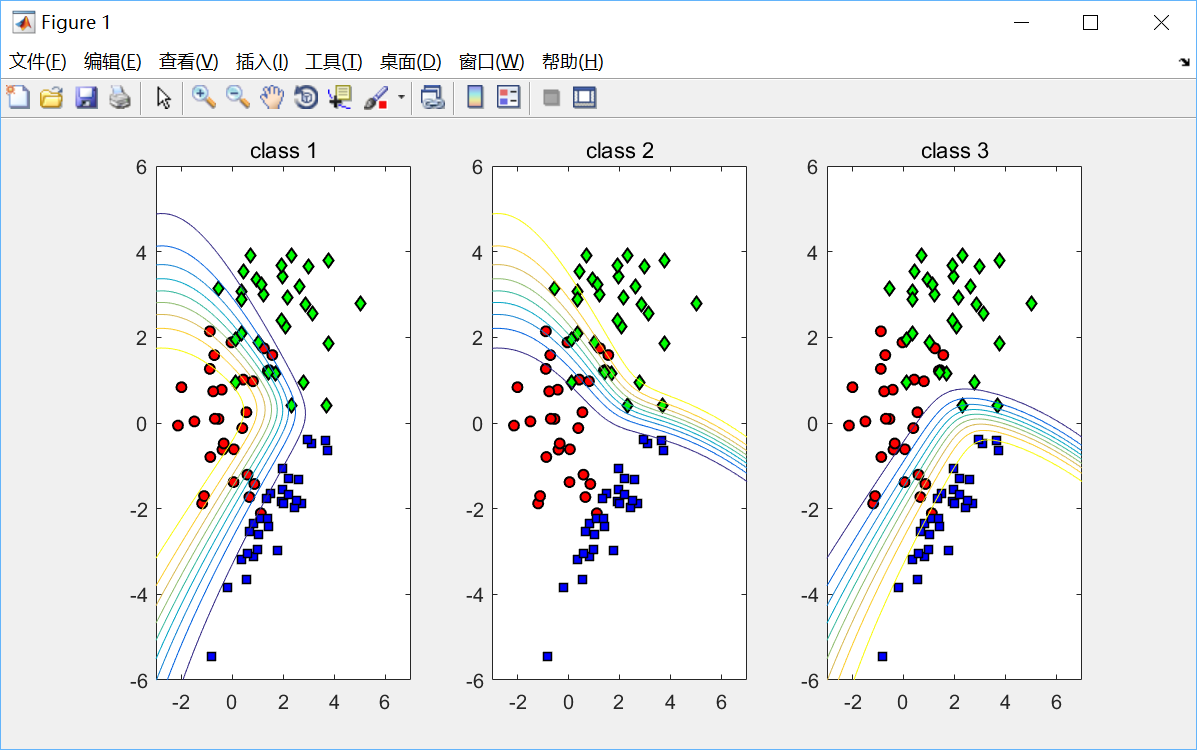
所有的多类分类问题都可分解为一类和其他类的二类分类子问题。由图可见分类边界都不是特别明确的,每一条曲线都有一定的决策把握度,即分类概率,越靠近某一类的内侧(如红色点)分类概率越高,在此空间出现的样本点可以有很大把握归为此类。
下面分析垃圾邮件分类器。
2.垃圾邮件分类器
此问题要建立的模型就稍微简单了,邮件分类就分为两类:spam or not spam.
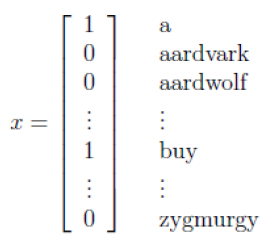
在上述基于高斯模型的贝叶斯分类器中,输入的特征向量x = [x1, x2, … , xn]是连续实数向量;在垃圾邮件分类中,我们输入的是离散的单词向量,即首先找一部英文词典,向量中每一维表示词典中的每一个单词是否在此邮件中出现,出现为1,不出现为0。比如一封邮箱中出现了”a”和”buy”,没有出现”aardvark”, “aardwolf”, “zygmurgy”,可以形式的表示为:
假如词典中有50000个词,那么向量x是50000维的,此时可以假设其服从另一种分布——多项分布。
(1)多项分布
多项分布是二项分布的扩展。某随机实验如果有k个可能结局A1、A2、…、Ak,分别将他们的出现次数记为随机变量X1、X2、…、Xk,它们的概率分布分别是p1,p2,…,pk,那么在n次采样的总结果中,A1出现n1次、A2出现n2次、…、Ak出现nk次的这种事件的出现概率P有下面公式:
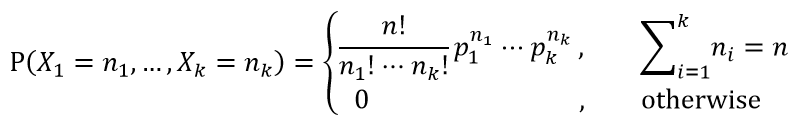
在本例中pk即可表示第k个词的概率,并且Σpk = 1.
(2)朴素贝叶斯假设
但是实际上,把每封邮件当作一次随机试验,则可能的结果有2^50000种,这是一个非常可怕的数目,不可能直接用来建模。因此又要使用利器——朴素贝叶斯假设,假设每个单词之间在一封邮件中出现是相互独立的。通常一封邮件中出现”buy”的时候,很有可能出现”price”这个词,因为这极有可能是一封推销邮件,肯定比其他一些完全不相干的单词出现的概率高。但作出朴素贝叶斯假设的时候,”buy”和”price”是否在一封邮件中同时出现就无关了。如下式所示:
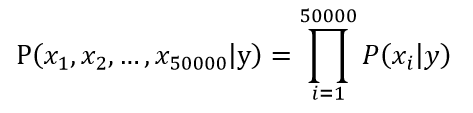
以此假设为基础,我们得到类条件分布的参数:
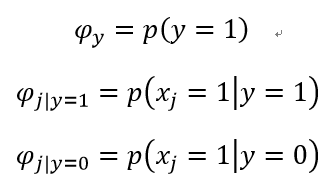
求其最大似然估计:
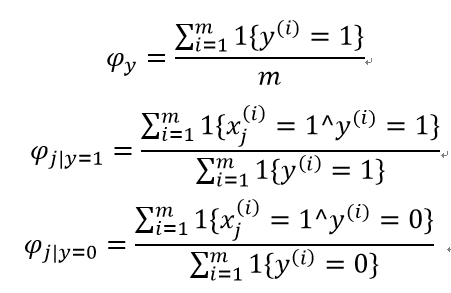
对于新样本,按照如下公式计算其概率值:
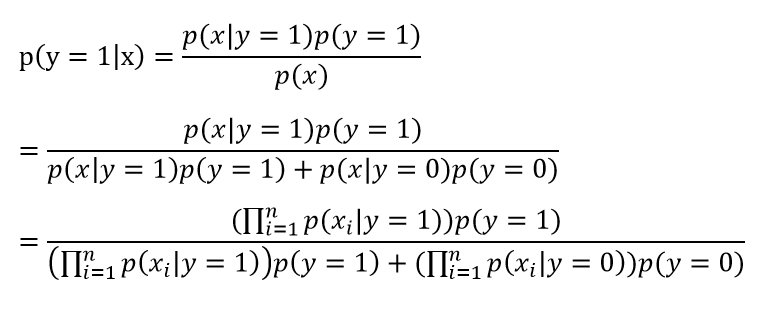
实际上只需计算出分子即可,分母对于每种类别都是相等的。
(3)拉普拉斯平滑
假如有一封新邮件,里面出现了一个词NIPS从未在训练数据中出现过,会导致整个实例的计算结果为零。为了解决这个问题,对于本例,可在原来的公式中分子加1,分母加2(类别数)。这就是拉普拉斯平滑法,其实平滑方法有很多种。
(4)代码实现:
鉴于Python的文本处理能力比较强大,此算法使用Python实现。
1)创建词汇表向量:
## 创建词汇表向量
def createVocabList(dataSet):
vocabSet = set([]) # 创建一个空集
for document in dataSet:
vocabSet = vocabSet | set(document) # 创建两个集合的并集
return list(vocabSet)2)创建词汇表特征向量:
## 创建词袋模型的词汇表特征向量,向量中的每一个元素表示文档中该单词的出现次数,输入参数是文档向量和词汇表向量
def bagOfWords2VecMN(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec
3)朴素贝叶斯训练函数:
## 朴素贝叶斯训练函数,输入文档向量和类别向量,返回类别1的单词概率向量,类别0的单词概率向量,以及垃圾邮件的概率
def trainNB0(trainMatrix,trainCategory):
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
pAbusive = sum(trainCategory) / float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords) # 此处为拉普拉斯平滑
p0Denom = 2.0; p1Denom = 2.0 # 此处为拉普拉斯平滑
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom) # 转化为对数运算,防止计算结果太过接近于0
p0Vect = log(p0Num/p0Denom)
return p0Vect, p1Vect, pAbusive4)朴素贝叶斯分类函数:
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + log(pClass1)
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 05)把文档切分成单词向量:
def textParse(bigString):
import re
listOfTokens = re.split(r'\W*', bigString)
return [tok.lower() for tok in listOfTokens if len(tok) > 2] 6)测试函数;测试样本中有25封垃圾邮件和25封正常邮件。其中10封邮件被随机选择为训练集,同时把它们从原样本中剔除。以此训练出来的模型对余下邮件进行分类,同时计算分类器的错误率。
def spamTest():
docList=[]; classList = []; fullText =[]
for i in range(1,26):
wordList = textParse(open('email/spam/%d.txt' % i).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(1)
wordList = textParse(open('email/ham/%d.txt' % i).read())
docList.append(wordList)
fullText.extend(wordList)
classList.append(0)
vocabList = createVocabList(docList)# 创建词汇表
trainingSet = list(range(50)); testSet=[] #创建测试集
for i in range(10):
randIndex = int(random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat=[]; trainClasses = []
for docIndex in trainingSet:#训练样本
trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V,p1V,pSpam = trainNB0(array(trainMat),array(trainClasses))
errorCount = 0
for docIndex in testSet: # 对余下的样本进行分类
wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
if classifyNB(array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
errorCount += 1
print("classification error",docList[docIndex])
rate = float(errorCount) / len(testSet)
print('the error rate is: ', rate)
return rate
sum = 0
n = 100
for i in range(n):
rate = bayes.spamTest()
sum += rate
average = sum / float(n)
print('The average of error rate is %f ' % average)
测试结果如下:

由于训练集是随机选择的,所以每次的输出结果可能有些差别。如果发现分类错误的话,函数会输出错分文档的单词表,这样就可以知道哪篇文档发生了错误。测试平均错误率为7%左右。
三、总结
对于分类而言,很多时候使用概率模型要比使用一些硬规则有效,个人感觉是比较温和的方法,不像Logistic回归直接画一条线分开这么粗暴。所谓的“朴素”,其实就是独立性假设,本文介绍的两种模型都很好地使用了这个假设,降低了对数据量的需求。但这个假设往往会造成输出模型过于简单,失去一定的灵活性。尽管条件独立性假设并不一定正确,但是建立起来的朴素贝叶斯模型仍然可以发挥它的作用。小小一条贝叶斯公式,看似平淡无奇,实则暗含巨大的力量。科学的力量是无穷的。这股力量鼓励着人类不断前行,不断进步!