题意:传送门
题解:这个题想了半天不知道如何下手,看了题解
题解一:首先考虑对于一个字符串,如果要拆成 n n n个’AB’串, m m m个’BA’串,那么贪心来做,考虑前面的’A’,首先给了’AB’来用,再给了‘BA’来用,对于’B‘也是这个道理,先给’BA’用,再给‘AB’用。然后就能考虑使用DP来做了,考虑 f [ i ] [ j ] f[i][j] f[i][j]表示前缀中用了 i i i个’A’,用了 j j j个’B’的方案数,考虑如何转移,如果 i < n ∣ ∣ ( i − n ) < m i n ( j , m ) i<n||(i-n)<min(j,m) i<n∣∣(i−n)<min(j,m),那么 f [ i + 1 ] [ j ] + = f [ i ] [ j ] f[i+1][j]+=f[i][j] f[i+1][j]+=f[i][j],如果 j < m ∣ ∣ ( j − m ) < m i n ( i , n ) j<m||(j-m)<min(i,n) j<m∣∣(j−m)<min(i,n),那么 f [ i ] [ j + 1 ] + = f [ i ] [ j ] f[i][j+1]+=f[i][j] f[i][j+1]+=f[i][j],最后输出 f [ n + m ] [ n + m ] f[n+m][n+m] f[n+m][n+m]即可。
#include<bits/stdc++.h>
#define sc2(a,b) scanf("%d%d",&a,&b)
#define mm(a,b) memset(a,b,sizeof(a))
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define per(i,a,b) for(int i=(a);i>=(b);i--)
using namespace std;
const int N=2*1e3+5;
const int P=1e9+7;
int n,m,f[N][N];
int main()
{
while(sc2(n,m)==2){
f[0][0]=1;
rep(i,0,n+m)rep(j,0,n+m){
if(i<n||i-n<min(j,m))f[i+1][j]=(f[i+1][j]+f[i][j])%P;
if(j<m||j-m<min(i,n))f[i][j+1]=(f[i][j+1]+f[i][j])%P;
}
printf("%d\n",f[n+m][n+m]);
rep(i,0,n+m+1)rep(j,0,n+m+1)f[i][j]=0;
}
return 0;
}
另外一种方法就是使用刷表法一样的东西,考虑一共要放 2 ∗ ( n + m ) 2*(n+m) 2∗(n+m)轮,然后放一个’A’标志 − 1 -1 −1,放一个’B’标志 + 1 +1 +1,用 d p [ i ] [ j ] dp[i][j] dp[i][j]表示当前放了 i i i个字符,标记为 j j j的方案数,对于标记 j j j可以使用一个坐标移位的小 t r i c k trick trick,考虑标记中把不合法的轮轮去掉,最后答案就是 d p [ 2 ∗ ( n + m ) ] [ E ] dp[2*(n+m)][E] dp[2∗(n+m)][E]了,当然此轮只与上一轮有关,那么用个滚动数组再次优化空间和时间。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e3+5;
const int P=1e9+7;
const int E=1e3;
ll n,m,f[N*4][N*3];
void add(ll &x,ll y)
{
x+=y;if(x>=P)x-=P;
}
int main()
{
while(scanf("%lld%lld",&n,&m)==2){
f[0][E]=1;
for(int i=1;i<=2*(n+m);i++)for(int j=E-n;j<=E+m;j++){
if(j>E-n)add(f[i][j-1],f[i-1][j]);
if(j<E+m)add(f[i][j+1],f[i-1][j]);
}
printf("%lld\n",f[2*(n+m)][E]);
for(int i=0;i<=2*(n+m);i++)for(int j=E-n;j<=E+m;j++)f[i][j]=0;
}
return 0;
}
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e3+5;
const int P=1e9+7;
const int E=1e3;
ll n,m,f[2][N*3];
void add(ll &x,ll y)
{
x+=y;if(x>=P)x-=P;
}
int main()
{
while(scanf("%lld%lld",&n,&m)==2){
memset(f,0,sizeof(f));
f[0][E]=1;
for(int i=1;i<=2*(n+m);i++){
int o=i&1;
for(int j=E-n;j<=E+m;j++){
if(j>E-n)add(f[o][j-1],f[o^1][j]);
if(j<E+m)add(f[o][j+1],f[o^1][j]);
f[o^1][j]=0;
}
}
printf("%lld\n",f[0][E]);
}
return 0;
}
最后又发现了一种方法就是这个问题其实是一个卡特兰数的变形问题,仍然哪个贪心构造答案的想法还是得想到,然后考虑一共有 2 ∗ ( n + m ) 2*(n+m) 2∗(n+m)个字符,然后从中选取 n + m n+m n+m个A,也就是 C ( n + m 2 ( n + m ) ) C\binom{n+m}{2(n+m)} C(2(n+m)n+m),减去不合法的方案数就是答案,那么对于每个时刻有两个限制条件就是
y ≤ x + n y\le x+n y≤x+n
x ≤ y + m x\le y+m x≤y+m
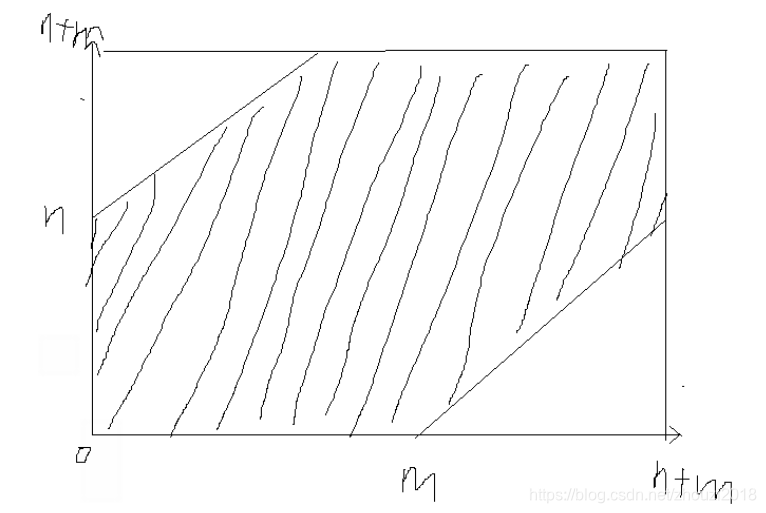
这样利用卡特兰数的算法直接可以推导出公式: C ( n + m 2 ( n + m ) ) − C ( n − 1 2 ( n + m ) ) − C ( m − 1 2 ( n + m ) ) C\binom{n+m}{2(n+m)}-C\binom{n-1}{2(n+m)}-C\binom{m-1}{2(n+m)} C(2(n+m)n+m)−C(2(n+m)n−1)−C(2(n+m)m−1)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=4e3+5;
const int M=1e9+7;
ll f[N],nf[N],inv[N];
void init()
{
inv[1]=1; for (int i=2;i<N;i++) inv[i]=M-(M/i)*inv[M%i]%M;
f[0]=nf[0]=1; for (int i=1;i<N;i++) f[i]=f[i-1]*i%M,nf[i]=nf[i-1]*inv[i]%M;
}
ll C(ll x,ll y)
{
return f[x]*nf[y]%M*nf[x-y]%M;
}
int n,m;
int main()
{
init();
while(scanf("%d%d",&n,&m)==2){
ll ans=C(2*(n+m),n+m);
ans=(ans-C(2*(n+m),n-1)+M)%M;
ans=(ans-C(2*(n+m),m-1)+M)%M;
printf("%lld\n",ans);
}
return 0;
}