Inductive and Unsupervised Representation Learning on Graph Structured Objects

• 论文地址：https://openreview.net/pdf?id=rkem91rtDB
• 源码：SEED-reimplementation
• 来源：ICLR, 2020
• 关键词：unsupervised learning, graph representation,

1 前言

该论文主要解决的是图结构数据的无监督的、inductive形式的表征问题。通常在无监督的图表征问题中，主要以重建损失为主导进行训练，但是在计算重建损失时通常要涉及到图的相似性计算，而图的相似性计算是一个十分复杂、耗时的过程，论文提出了一个通用的框架SEED（Sampling, Encoding and Embedding Distribution）用于无监督的学习图结构对象的表征。

2 问题定义

目标很简单，给定一个graph，学习它的表征。

3 SEED思路

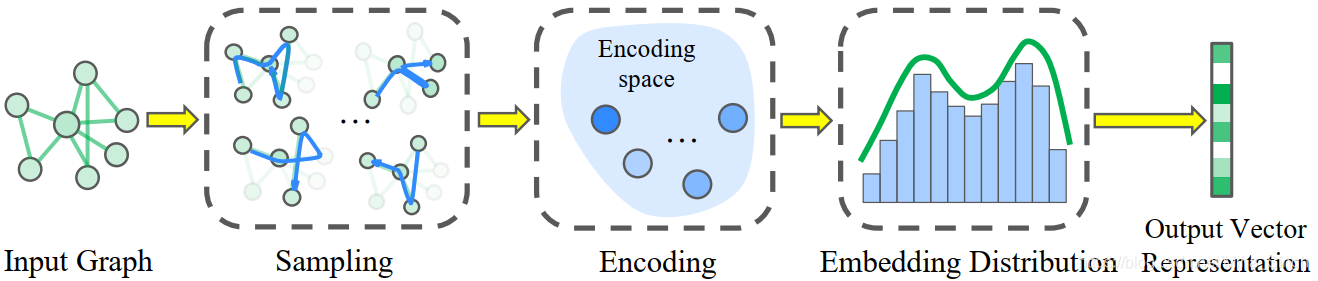
如上图所示所示，SEED主要分为三个部分：

3.1 Sampling

从输入的图中采样出多个子图。为了使得采样到的子图更具代表性，论文中提出了一种新的采样方法 — WEAVE（random Walk with EArliest Visit timE）。该方法与通常的随机游走不一样，WEAVE是带结点访问时间戳的。

如上图所示，WEAVE的区分能力比平凡的搜集游走更强。每一个WEAVE都代表一个采样到的子图，可以用一个矩阵表示：$X=\left[{\mathbf{x}}^{(0)},{\mathbf{x}}^{(1)},\cdots ,{\mathbf{x}}^{(k)}\right]$，其中${\mathbf{x}}^{(p)}=[{\mathbf{x}}_a^{(p)},{\mathbf{x}}_t^{(p)}]$，${\mathbf{x}}_a^{(p)}$表示在时间$p$时访问到的结点的特征，${\mathbf{x}}_t^{(p)}$表示访问到该结点时的时间向量。注意，如果访问到了已经访问过的结点则${\mathbf{x}}_t^{(p)}$为最早访问时的时间。在论文中，${\mathbf{x}}_t^{(p)}$采用one-hot编码。

3.2 Encoding

将每一个采样到的子图编码为向量。直觉上，如果子图的表征质量好，那么就能在子图表征地基础上较好地重建子图。论文中作者采样自编码器学习子图的表征，以重建损失作为损失函数。至此，$s$个子图 { X 1 , . . . , X s } \{X_1, ..., X_s\} { X1​,...,Xs​}被表示为$s$个向量 { z 1 , . . . , z s } \{\mathbf{z}_1, ..., \mathbf{z}_s\} { z1​,...,zs​}。

3.3 Embedding Distribution

将上一阶段获得的多个子图的表征汇集作为输入图的表征。对于两个图，它们在表征空间中的距离应该与它们的子图向量分布距离类似，因此需要找到一个好的聚集函数来保留原先的子图表征分布距离，论文中采用的是$MMD$。
给定连个图$\mathcal{G},\mathcal{H}$，子图表征分别为： { z 1 , . . . , z s } \{\mathbf{z}_1, ..., \mathbf{z}_s\} { z1​,...,zs​}和 { h 1 , . . . , h s } \{\mathbf{h}_1, ..., \mathbf{h}_s\} { h1​,...,hs​}，则两者间的$MMD$为：
$$\begin{array}{rl}\widehat{MMD}\left(P_{\mathcal{G}},P_{\mathcal{H}}\right)=& \frac{1}{s(s-1)}\sum _{i=1}^s\sum _{j\ne i}^{s}k\left({\mathbf{z}}_i,{\mathbf{z}}_j\right)+\frac{1}{s(s-1)}\sum _{i=1}^s\sum _{j\ne i}^{s}k\left({\mathbf{h}}_i,{\mathbf{h}}_j\right)\\ & -\frac{2}{s^2}\sum _{i=1}^s\sum _{j=1}^{s}k\left({\mathbf{z}}_i,{\mathbf{h}}_j\right)\\ =& {\Vert {\hat{\mu }}_{\mathcal{G}}-{\hat{\mu }}_{\mathcal{H}}\Vert }_2^2\end{array}$$
${\hat{\mu }}_{\mathcal{G}},{\hat{\mu }}_{\mathcal{H}}$分别表示两个图的kernel embedding，也就是最终的graph representation，分别定义为：
$${\hat{\mu }}_{\mathcal{G}}=\frac{1}{s}\sum _{i=1}^s\varphi \left({\mathbf{z}}_i\right),{\hat{\mu }}_{\mathcal{H}}=\frac{1}{s}\sum _{i=1}^s\varphi \left({\mathbf{h}}_i\right)$$
其中$\varphi (\cdot )$是与核函数$k(\cdot ,\cdot )$相关的特征映射函数（与SVM中的核技巧类似，将核函数的计算转化为更简单的计算形式）。
根据核函数的选择，$\varphi (\cdot )$具有不同的形式，如RBF、MLP等。为了训练$\varphi (\cdot )$，文中使用如下的近似误差，其中${\theta }_m$为$\varphi (\cdot )$的参数）：
$$J\left({\theta }_m\right)={\Vert D\left(P_{\mathcal{G}},P_{\mathcal{H}}\right)-\widehat{MMD}\left(P_{\mathcal{G}},P_{\mathcal{H}}\right)\Vert }_2^2$$
通过最小化上述误差，就能学习到较好的聚集函数，在最终的表征中保留子图表征的分布距离。

该论文的方法与核方法有一定的相似性。论文还证明了同构的图的WEAVE的子图分布是类似的，并且对子图的采样长度进行了证明，详细内容可以参考论文。

4 方法的优势与局限性

4.1 优势

• 给出了无监督形式的、inductive的图结构对象表征学习方法
• 避免了复杂的图相似性计算，以类似于核技巧的方法较好地度量了图之间地距离
• 对相关地定理进行了证明

4.2 局限性

• 当图地规模较大时，采样的子图也会非常大，且可能需要采样地子图数量会很大

---

---

欢迎访问我的个人博客~~~