反向传播算法(Backpropagation)----Gradient Descent的推导过程

BP算法是适用于多层神经网络的一种算法，它是建立在梯度下降法的基础上的。本文着重推导怎样利用梯度下降法来minimise Loss Function。

给出多层神经网络的示意图：

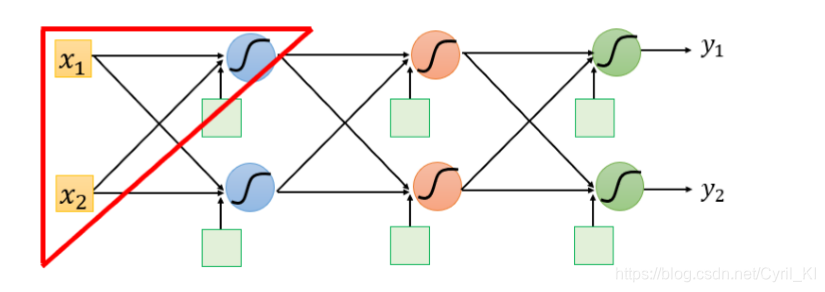
1.定义Loss Function

假设有一组数据样本 $x^{1}$， $x^{2}$，… ，每一个x都有很多个特征，输入x，会得到一个输出y，每一个输出都对应一个损失函数L，将所有L加起来就是total loss。
那么每一个L该如何定义呢？这里还是采用了交叉熵，如下所示：

这里的 $y^{i}$是真实输出， $y\hat{}$是y target，是人为定义的。最终Total Loss的表达式如下：

2.Gradient Descent

L对应了一个参数，即Network parameters θ(w1,w2…b1,b2…)，那么Gradient Descent就是求出参数 $\theta^{*}$来minimise Loss Function，即：

梯度下降的具体步骤为：

3.求偏微分

从上图可以看出，这里难点主要是求偏微分，由于L是所有损失之和，因此我们只需要对其中一个损失求偏微分，最后再求和即可。
先抽取一个简单的神经元来解释：
先理一理各个变量之间的关系：我们要求的是Total Loss对参数w的偏导，而Total Loss是一个个小的l累加得到的，因此，我们只需要求得 $\frac{\partial l}{\partial w}$，而 $l=-\hat{y}lny$，其中 $\hat{y}$是人为定义的，跟w没有关系，因此我们只需要知道 $\frac{\partial y}{\partial w}$。l跟z有关系，根据链式求导法则，我们需要求 $\frac{\partial l}{\partial z}$和 $\frac{\partial z}{\partial w}$，其中 $\frac{\partial z}{\partial w}$的求解较为容易，如下图所示：

求 $\frac{\partial l}{\partial z}$是一个难点，因为我们并不知道后面到底有多少层，也不知道情况到底有多复杂，我们不妨先取一种最简单的情况，如下所示：

4.反向传播

在第一张图里面，我们经过正向传播很容易求出了 $\frac{\partial z}{\partial w}$，而对于 $\frac{\partial l}{\partial z}$，则并不是那么好求。上图其实就是运用了反向传播的思想， 对于上图中 $\frac{\partial l}{\partial z}$最后的表达式，我们可以换一种结构，如下所示：

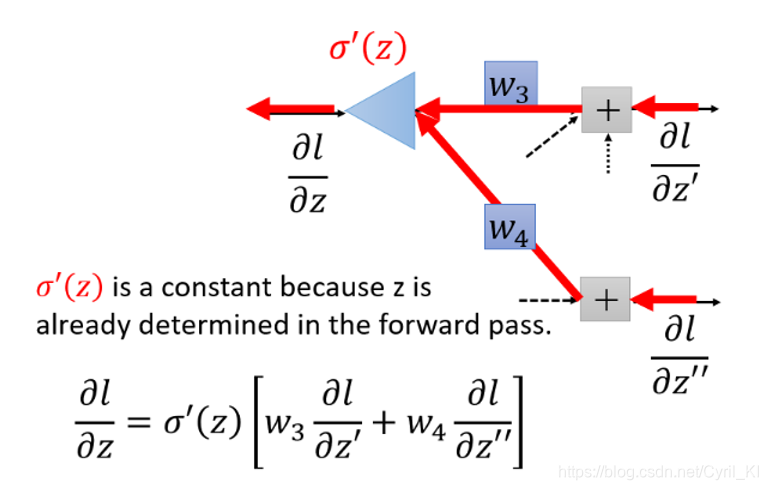
l对两个z的偏导我们假设是已知的，并且在这里是作为输入，三角形结构可以理解为一个乘法运算电路，其放大系数为 $\sigma {}'(z)$。但是在实际情况中，l对两个z的偏导是未知的。假设神经网络最终的结构就是如上图所示，那么我们的问题已经解决了：

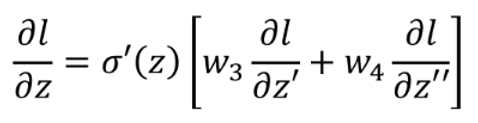
其中：

但是假如该神经元不是最后一层，我们又该如何呢？比如又多了一层，如下所示：

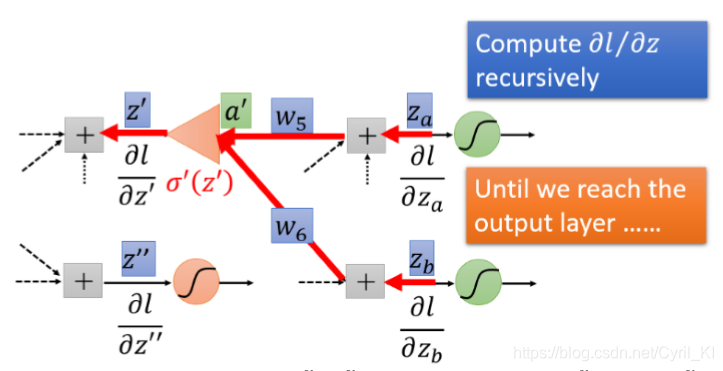
那么我们只要知道 $\frac{\partial l}{\partial z_{a}}$和 $\frac{\partial l}{\partial z_{b}}$，我们同样可以算出 $\frac{\partial l}{\partial z{}'}$以及 $\frac{\partial l}{\partial z{}''}$，原理跟上面类似，如下所示：

$\frac{\partial l}{\partial z_{b}}$同样是l先对y求导，y再对 $z_{b}$求导。

那假设我们再加一层呢？再加两层呢？再加三层呢？。。。，情况还是一样的，还是先求l对最后一层z的导数，乘以权重相加后最后再乘上 $\sigma {}'(z{}'',z{}''',...)$即可。
最后给一个实例：

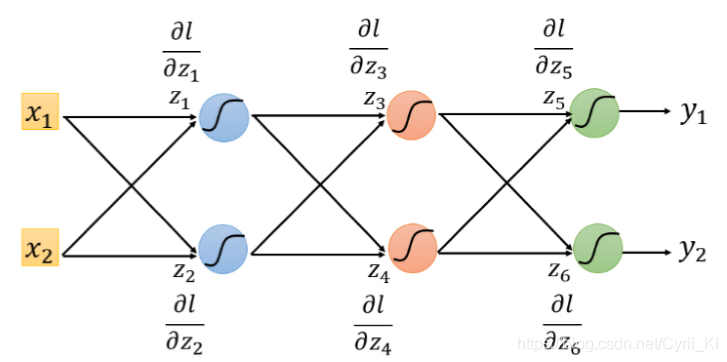
它的反向传播图长这样：

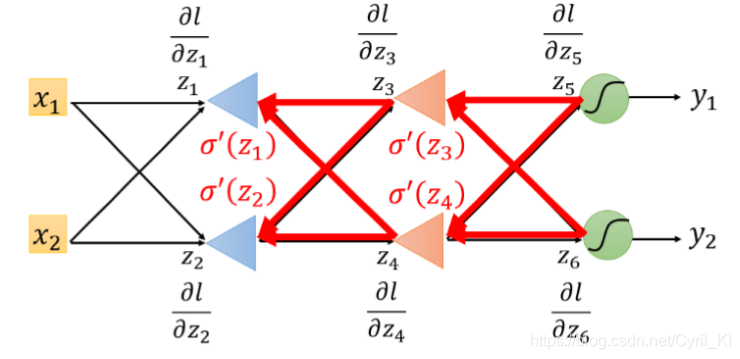
我们可以很轻松的算出 $\frac{\partial l}{\partial z_{5}}$和 $\frac{\partial l}{\partial z_{6}}$，算出这两个之后，根据上面我们找到的关系式，我们也可以轻易算出 $\frac{\partial l}{\partial z_{3}}$和 $\frac{\partial l}{\partial z_{4}}$，最后再算出 $\frac{\partial l}{\partial z_{1}}$和 $\frac{\partial l}{\partial z_{2}}$。然后 $\frac{\partial l}{\partial z_{1}}$和 $\frac{\partial l}{\partial z_{2}}$再分别乘上x1和x2，就是我们最终要找的 $\frac{\partial l}{\partial w_{1}}$和 $\frac{\partial l}{\partial w_{2}}$。
我们不难发现，这种计算方式很清楚明了地体现了“反向传播”四个字。
好了，目标达成！！

5.总结

通过Forward Pass我们求得 $\frac{\partial z}{\partial w}=a$，然后通过Backward Pass我们求得 $\frac{\partial l}{\partial z}$，二者相乘，就是 $\frac{\partial l}{\partial w}$。利用上述方法求得所有参数的值之后，我们就可以用梯度下降法来更新参数，直至找到最优解。