梯度下降法(Gradient Descent)推导和示例
注:作者在其他文献的基础上进行整理,形成本文的基本脉络,并希望通过较为简单清晰的推导过程来帮助新手入门
本文主要由以下部分组成:
- 梯度下降法合理性证明
- 单变量示例
- 多变量示例
- 矩阵化表示
首先我们先给出梯度的定义。某一函数沿着某点处的方向导数可以以最快速度到达极大值,该方向导数我们定义为该函数的梯度。
其中θ是自变量,f(θ)是关于θ的函数,▽表示梯度。
我们要研究的梯度下降式子可以写作:
其中η是步长,θ是由θ0按照上述式子更新后的值。
· 梯度下降法合理性证明
在给出具体的证明之前,我们可以先直观感受梯度下降法的含义:

假设我们位于某山的某个山腰处,山势连绵不绝,不知道怎么下山。于是决定走一步算一步,也就是每次沿着当前位置最陡峭最易下山的方向前进一小步,然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去,一直走到觉得我们已经到了山脚。这里的下山最陡的方向就是梯度的负方向。通过这个例子,我们可以在直观上感受到梯度下降法的合理性。
首先我们给出一阶的泰勒展开式:
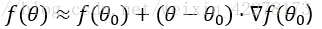
在泰勒公式中,我们为了保证该式成立,最重要的一点是要保证θ和θ0的差距要足够小,只有这样才能够应用泰勒公式的基本思想“以直代曲”。为了便于说明,我们在一个三维空间里面去做证明。并且把自变量具体化:
θ=(x,y)
θ0=(x0,y0)

这个图将小量画比较大,是为了更好地说明问题。因此通过泰勒公式我们可以得到:


· 单变量示例
· 多变量示例




