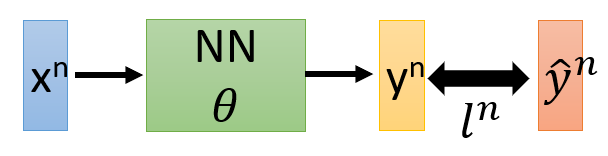[Deep Learning] 反向传播算法（Backpropagation Algorithm）

Chain Rule（链式法则）

---

Case 1

如果有：

$y = g(x)\ \ \ \ \ \ z = h(y)$

那么“变量影响链”就有：

$\Delta x\rightarrow \Delta y \Delta z$

因此就有：

$\frac{d z}{d x} = \frac{d z}{d y}\frac{d y}{d x}$

Case 2

如果有：

$y = g(s)\ \ \ \ \ \ y = h(s)\ \ \ \ \ \ z=k(x,y)$

那么“变量影响链”就有：

因此就有：

$\frac{d z}{d s} = \frac{\partial z}{\partial x}\frac{d x}{ds} + \frac{\partial z}{\partial y}\frac{d y}{ds}$

Backpropagation（反向传播算法）——实例讲解

---

定义

反向传播（英语：Backpropagation，缩写为BP）是“误差反向传播”的简称，是一种与最优化方法（如梯度下降法）结合使用的，用来训练人工神经网络的常见方法。 该方法对网络中所有权重计算损失函数的梯度。 这个梯度会反馈给最优化方法，用来更新权值以最小化损失函数。（误差的反向传播）——维基百科

说明

假设现在有N个样本数据，那么实际上损失函数可以表示为：

$L(\theta) = \sum_{n=1}^Nl^n(\theta)$

其中 $\theta$为需要学习的参数。

那么现在 $\omega$对 $L$进行偏微分，实际上是对每个样本数据的损失函数 $l(\theta)$进行偏微分后再求和：

$\frac{\partial L(\theta)}{\partial \omega} = \sum_{n=1}^N\frac{\partial l^n(\theta)}{\partial \omega}$

用代数表示为：

$z_1 = \omega_{11}x_1 + \omega_{12}x_2 + b_1 \ \ \ \ \ \ \ \ \ \ \ a_1 = \sigma(z_1)$

$z_2 = \omega_{21}x_1 + \omega_{22}x_2 + b_2 \ \ \ \ \ \ \ \ \ \ \ a_2 = \sigma(z_2)$

$z_3 = \omega_{31}a_1 + \omega_{32}a_2 + b_3 \ \ \ \ \ \ \ \ \ \ \ a_3 = \sigma(z_3)$

$z_4 = \omega_{41}a_1 + \omega_{42}a_2 + b_4 \ \ \ \ \ \ \ \ \ \ \ a_4 = \sigma(z_4)$

$z_5 = \omega_{51}a_3 + \omega_{52}a_4 + b_5 \ \ \ \ \ \ \ \ \ \ \ y_1 = \sigma(z_5)$

$z_6 = \omega_{61}a_3 + \omega_{62}a_4 + b_6 \ \ \ \ \ \ \ \ \ \ \ y_2 = \sigma(z_6)$

那么我们实际要计算的是：

$\frac{\partial l}{\partial \omega} = \frac{\partial z}{\partial \omega}\frac{\partial l}{\partial z}$

即分别计算出 $\frac{\partial z}{\partial \omega}$和 $\frac{\partial l}{\partial z}$:

Step 1：Forward Pass

这个过程实际上是计算Neural Network的所有 $\frac{\partial z_i}{\partial \omega_{i1}}$和 $\frac{\partial z_i}{\partial \omega_{i2}}$，即：

$\frac{\partial z_1}{\partial \omega_{11}} = x_1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial z_1}{\partial \omega_{12}} = x_2$

$\frac{\partial z_2}{\partial \omega_{21}} = x_1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial z_2}{\partial \omega_{22}} = x_2$

$\frac{\partial z_3}{\partial \omega_{31}} = a_1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial z_3}{\partial \omega_{32}} = a_2$

$\frac{\partial z_4}{\partial \omega_{41}} = a_1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial z_4}{\partial \omega_{42}} = a_2$

$\frac{\partial z_5}{\partial \omega_{51}} = a_3 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial z_5}{\partial \omega_{52}} = a_4$

$\frac{\partial z_6}{\partial \omega_{61}} = a_3 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\partial z_6}{\partial \omega_{62}} = a_4$

如果用具体数值表示的话，那就是下图所示：

因为这个过程必须从输入 $x_1$、 $x_2$开始到输出，否则无法计算出之后的 $a_1$、 $a_2$、 $a_3$、 $a_4$，所以这个过程叫做Forward Pass。

Step 2：Backward Pass

这个过程是计算 $\frac{\partial l}{\partial z}$的过程，如果我们按照Step 1中的过程来计算的话，就会有如下过程：

$\frac{\partial l}{\partial z_1} = \frac{\partial a_1}{\partial z_1}\frac{\partial l}{\partial a_1}$

其中，

$\frac{\partial a_1}{\partial z_1} = \sigma'(z_1)$

$\frac{\partial l}{\partial a_1} = \frac{\partial z_3}{\partial a_1}\frac{\partial l}{\partial z_3}+\frac{\partial z_4}{\partial a_1}\frac{\partial l}{\partial z_4} = \omega_{31}\frac{\partial l}{\partial z_3} + \omega_{41}\frac{\partial l}{\partial z_4}$

即：

$\frac{\partial l}{\partial z_1} = \sigma'(z_1)(\omega_{31}\frac{\partial l}{\partial z_3} + \omega_{41}\frac{\partial l}{\partial z_4})$

同理，有：

$\frac{\partial l}{\partial z_2} = \sigma'(z_2)(\omega_{32}\frac{\partial l}{\partial z_3} + \omega_{42}\frac{\partial l}{\partial z_4})$

因此，如果我们要计算出 $\frac{\partial l}{\partial z_1}$和 $\frac{\partial l}{\partial z_2}$，我们还要先计算 $\frac{\partial l}{\partial z_3}$和 $\frac{\partial l}{\partial z_4}$，可以想象出来，我们再计算 $\frac{\partial l}{\partial z_3}$和 $\frac{\partial l}{\partial z_4}$的过程中，肯定还要计算 $\frac{\partial l}{\partial z_5}$和 $\frac{\partial l}{\partial z_6}$…

没错，这是一个递归过程！这还只是个比较简单的例子，如果是比较复杂的深度神经网络的话，时间复杂度必然是很高的，所以说，不能用Forward Pass的方法计算 $\frac{\partial l}{\partial z}$！

（重点来了！！！）

现在，如果你仔细端详 $\frac{\partial l}{\partial z_1} = \sigma'(z_1)(\omega_{31}\frac{\partial l}{\partial z_3} + \omega_{41}\frac{\partial l}{\partial z_4})$ 这个式子，你会发现，式子的形式是不是很像神经元的形式： $\frac{\partial l}{\partial z_3}$和 $\frac{\partial l}{\partial z_4}$作为输入， $\omega_{31}$和 $\omega_{41}$作为权重，而 $\sigma'(z_1)$可以看作是一个数值放大器，放大了 $\omega_{31}\frac{\partial l}{\partial z_3} + \omega_{41}\frac{\partial l}{\partial z_4}$的结果！如下图：

因此，计算 $\frac{\partial l}{\partial z}$的过程可以用如下图来表示：

这种方法就是Backward Pass，这样就不会出现刚才所说的递归了！

summary

通过Forward Pass计算得到的 $\frac{\partial z}{\partial \omega}$以及Backward Pass计算得到的 $\frac{\partial l}{\partial z}$，就可以得到 $\frac{\partial l}{\partial \omega}$

至此，“反向传播算法”及公式推导的过程总算是结束啦！我觉得这种思路还是比较好接受的，毕竟是受了“大木博士”的熏陶哈哈。