数学分析与概率论概要笔记

数学分析与概率论

目录：

引例：e的引入：

关于该函数极限收敛于e的证明：

附：

细节1的说明：

符合极限运算法则的定理三推论1的应用：

细节2的说明：

符合两边加定理的应用：

01.导数：

常用公式：

应用1-幂指函数的解题套路：

X^x的极小值求解：

附：

细节1的说明：

1.隐含条件：t！=0。

2.等式左边为1/t*t’,当t’=0的时候，1/t不为0且t‘为0，所以等式左边为0，即右边等式也等于0。

3.而产生等式lnx+1=0得到对应的极值点的x取值。最后将x带回原式得到极小值t。

应用2-积分：

附：

细节1的说明：

等式左边为ln1，ln2，ln3…lnN的累加求和，而这些部分又看作为△x*lnx,△x=x±(x-1)=1。即1xln1，1xln2，1xln3…1xlnN为相邻点之间围成的矩形面积，而这些面积的累加又近似看成lnx与x正方向轴围成的面积，当x趋近于N时，即为lnx的积分在x→N时。

补：时间复杂度O(ln(N!))==O(NlnN)

细节2的说明：

分部积分定理的应用：

此题中的u=lnx，v’=1。而lnx的积分为x(lnx-1)。

02.Taylor展开式—近似计算：

​

附：

复杂函数的Taylor展开式求解过程：

​ https://blog.csdn.net/acceptedday/article/details/99757867

Taylor公式的应用——e^x的计算：

03.方向导数与梯度：

方向导数：是一个数；反映的是f(x,y)在P点沿方向L的变化率。

然后进行向量化转换：

​

当向量V与向量U同方向时，f(x,y)的方向导数最大化，即此时的f(x,y)的在方向上的变化速率最大。

即向量v=(∂f/∂x,∂f/∂y)可决定f(x,y)变化速率最大化的L方向。

梯度： 是一个向量，每个元素为函数对一元变量的偏导数（其大小为最大方向导数）。

04.古典概型：

累计分布(概率)函数与概率密度函数：

组合数：

引例——装箱问题：

解析过程如下：

附：

细节1的说明：

3件次品均看成独立不同的个体，进行分别装入的计算时采用排列的方法，而不采用组合法；而对于分组，同一组的产品则不考虑排列，采用组合法。

分组问题与组合数之间的关系：

组合数与信息熵之间的关系：

附:

细节1的说明：

因为n1,n2,n3…nk是N的划分项，所以ni从(i=0)到(i=k)的累加和等于N，得到化简式。

05.几何概型：

​

几何概型应用1—商品推荐：

解析过程如下：

06.贝叶斯公式—后验概率：

​

贝叶斯公式应用—中靶问题：

问题描述：

解析过程：

其他常见的贝叶斯概率问题均采用相同的套路(不用记公式系列^-）。

07.泊松分布与指数分布：

泊松分布：Poisson分布，是一种统计与概率论中常见的离散概率分布，由法国数学家Siméon-Denis Poisson在1838年发表。其适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数，电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。

泊松概率质量函数与e^x的泰勒展开式：

附：

细节1的说明：

等式两边除以e^x,得到一种新的概率质量函数式，有趣！其他复杂函数的泰勒展开式也可以采用相同的套路得到新的概率质量函数式噢。

泊松分布图像(λ=12):

​

泊松概率质量函数式的期望和方差：

泊松分布的累积分布函数:

​

泊松分布的应用场景：

附：

泊松分布概率质量函数与泊松累计分布函数的图像：

​

​

指数分布：在概率论和统计学中，指数分配（Exponential distribution）是一种连续概率分布。指数分配可以用来表示独立随机事件发生的时间间隔，比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔、中文维基百科新条目出现的时间间隔等等。

指数分布累计分布函数：

​

指数分布概率密度函数与累计分布函数的图像：

​

​

注意：

泊松分布是针对随机事件发生次数的定义的离散随机变量，而指数分布是针对随机事件发生的间隔时间定义的连续随机变量，这是二者最大的区别。

附：

关于泊松分布与指数分布的重新理解的笔记链接：

​ https://xijunlee.github.io/2016/12/28/2016-12-28-bo-song-fen-bu-yu-zhi-shu-fen-bu-de-zhong-xin-li-jie/

08.二项分布与几何分布：

二项分布：即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。(二项分布是把整体划分为2个部分，(n-k)和k项的发生情况«^-»）

二项分布的公式和E(x),D(X):

​

附:

细节1的说明：

有和我一样一开始没看懂的嘛？哈哈。

二项分布的理解推荐文章链接：

​ https://www.jianshu.com/p/6dac4fcfa629

几何分布：P(X = n) = (1 − p)^(n − 1)p，某事件直到第n次发生的概率。

几何分布的累积分布函数证明：

​

超几何分布：

​

超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出n个物件，成功抽出指定种类的物件的次数(不归还)。

在产品质量的不放回抽检中，若N件产品中有M件次品，抽检n件时所得次品数X=k，则P(X=k)=C(M，k)·C(N-M,n-k)/C(N,n)， C(a b)为古典概型的组合形式，a为下限，b为上限，此时我们称随机变量X服从超几何分布(hypergeometric distribution)

(1)超几何分布的模型是不放回抽样。

(2)超几何分布中的参数是M,N,n上述超几何分布记作X~H(N,n,M)。

09.无记忆性分布：

博客链接：

​ https://blog.csdn.net/acceptedday/article/details/99870398

10.指数族分布(The exponential family distribution)：

指数族分布 (The exponential family distribution),区别于指数分布（exponential distribution)。在概率统计中，若某概率分布满足下式，我们就称之属于指数族分布。


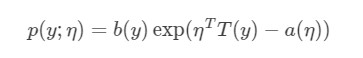
统计中很多熟悉的概率分布都是指数族分布的特定形式，如伯努利分布，高斯分布，多项分布（multionmal), 泊松分布等。下面介绍其中的伯努利分布和高斯分布。

伯努利分布与指数族分布：

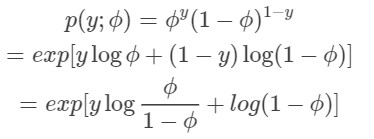
把伯努利分布可以写成指数族分布的形式，且

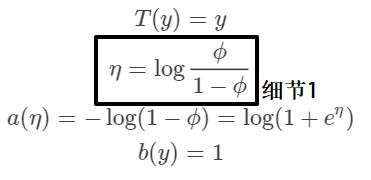
附：
细节1：
将等式进行变化，即得到sigmoid函数式：

高斯分布与指数族分布：

高斯分布式为**：

取δ=1，则进行指数族分布转换式：

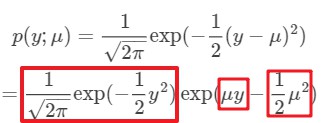
且各个部分的对应关系如下：

附：
指数族分布参考博客链接：
https://blog.csdn.net/u011467621/article/details/48197943