数学分析笔记12：傅里叶级数

函数的傅里叶级数

周期为 $2\pi$的函数的傅里叶级数

从纯数学的观点看，幂级数是对函数系 $1,x,x^2,x^3,\cdots$的线性组合，实际上，多项式是以上函数系的有限线性组合，幂级数是对以上函数系的可数线性组合。从这个观点看，更换一组函数系，就可以得到另一种级数，初等函数中具有周期性的典型的函数是三角函数，因此，自然想到采用三角函数系来构成新的级数形式 $1,\sin(x),\cos(x),\sin(2x),\cos(2x),\sin(3x),\cos(3x),\cdots$我们称级数 $f(x)=a_0+\sum_{n=1}^{\infty}(a_n\cos(nx)+b_n\sin(nx))$为傅里叶级数。显然，如果 $f(x)$可以展开成以上三角级数的形式，那么， $f(x)$应当是以 $2\pi$为周期的。反过来，我们要问：如果函数 $f(x)$是以 $2\pi$为周期的函数，满足何种条件下它能展开成三角级数的形式？如果能展开，各项系数应当如何确定呢？
我们首先假设 $\underline{f(x)能展开成三角级数的形式}$，并且假设可以进行 $\underline{逐项积分}$。那么我们可以通过逐项积分的形式求出各项系数。为什么呢？因为三角函数系具有 $\underline{正交性}$，是 $\underline{正交函数系}$。我们在解析几何和高等代数中接触了内积空间的概念，所谓内积，即满足 $\underline{对称、正定的双线性函数}$。对于 $[a,b]$上的可积函数 $f(x),g(x)$，定义内积为 $\displaystyle <f,g>=\int_a^b{f(x)g(x)dx}$，从解析几何的观点看，如果两个向量垂直或称正交，那么，两个向量的内积为0，在抽象的函数空间这里，我们也引入“正交”的概念，下面我们验证三角函数系在 $[-\pi,+\pi]$上是正交函数系。 $\int_{-\pi}^{\pi}{sin(nx)dx}=[-\frac{1}{n}cos(nx)]_{-\pi}^\pi=0,n=1,2,\cdots$ $\int_{-\pi}^\pi{cos(nx)dx}=[\frac{1}{n}sin(nx)]_{-\pi}^\pi=0,n=1,2,\cdots$ $\begin{aligned} \int_{-\pi}^\pi{\cos(ix)\cos(jx)dx}=\frac{1}{2}(\int_{-\pi}^\pi{cos((i+j)x)dx}+\int_{-\pi}^\pi{cos((i-j)x)dx})=0\\i\neq j,i,j=1,2,\cdots \end{aligned}$ $\begin{aligned} \int_{-\pi}^\pi{\sin(ix)\sin(jx)dx}=\frac{1}{2}(\int_{-\pi}^\pi{cos((i-j)x)dx}-\int_{-\pi}^\pi{cos((i+j)x)dx})=0\\i\neq j,i,j=1,2,\cdots \end{aligned}$ $\begin{aligned} \int_{-\pi}^\pi{\sin(ix)\cos(jx)dx}=\frac{1}{2}(\int_{-\pi}^\pi{sin((i-j)x)dx}+\int_{-\pi}^\pi{sin((i+j)x)dx})=0\\i,j=1,2,\cdots \end{aligned}$由正交性，要求 $\sin(nx),\cos(nx),1$对应的系数，只需要乘以相应的三角函数，再进行逐项积分即可。由于 $\int_{-\pi}^\pi{dx}=2\pi$ $\int_{-\pi}^\pi{\cos^2(nx)dx}=\int_{-\pi}^\pi{\frac{1+\cos(2nx)}{2}dx}=\pi$ $\int_{-\pi}^\pi{\sin^2(nx)dx}=\int_{-\pi}^\pi{\frac{1-\cos(2nx)}{2}dx}=\pi$两边乘以 $1$，再进行逐项积分，得到 $\int_{-\pi}^\pi{f(x)dx}=2\pi a_0$两边乘以 $\cos(nx)$，再进行逐项积分，得到
$\int_{-\pi}^\pi{f(x)\cos{(nx)}dx}=a_n\pi,n=1,2,\cdots$两边乘以 $\sin(nx)$，再进行逐项积分，得到 $\int_{-\pi}^\pi{f(x)\sin{(nx)}dx}=b_n\pi,n=1,2,\cdots$于是，我们就求解出所有系数。总结起来就是 $\begin{cases} a_0=\frac{1}{2\pi}\int_{-\pi}^\pi{f(x)dx}\\ a_n=\frac{1}{\pi}\int_{-\pi}^\pi{f(x)\cos{(nx)}dx}&n=1,2,\cdots\\ b_n=\frac{1}{\pi}\int_{-\pi}^\pi{f(x)\sin{(nx)}dx}&n=1,2,\cdots \end{cases}$这组系数称为傅里叶系数，实际上，如果 $f(x)$在 $[-\pi,\pi]$上可积，也可以求出这么一组系数，但 $f(x)$是否等于其傅里叶级数呢？答案是否定的。因为，如果仅仅改变 $f(x)$在 $[-\pi,\pi]$内的有限个点，傅里叶级数也是不变的，所以，我们只能称 $f(x)$对应于其傅里叶级数，而不能简单的划等号。我们记 $f(x)~a_0+\sum_{n=1}^\infty{a_n\cos(nx)+b_n\sin(nx)}$波浪号就表示对应，而不是采用等号，右边称为 $f(x)$的傅里叶级数。对于求傅里叶级数，我们给出一个命题，以方便我们选择最合适的区间来进行积分。

定理12.1 $f(x)$是 $(-\infty,+\infty)$上的以 $2T$为周期的函数， $f(x)$在任意有界闭区间上可积，则 $\forall \delta \in R$，有 $\int_{-T}^T{f(x)dx}=\int_{-T+\delta}^{T+\delta}{f(x)}dx$

证：
不失一般性，设 $\delta>0$，我们证明： $\displaystyle \int_{-T}^{-T+\delta}{f(x)dx}=\int_{T}^{T+\delta}{f(x)dx}$，令分划 $\Delta_n:T=x_0^{(n)}<x_1^{(n)}=T+\frac{\delta}{n}<\cdots<x_{n-1}^{(n)}=T+\frac{(n-1)\delta}{n}<x_n^{(n)}=T+\delta$，构造黎曼和 $S_n(x)=\frac{\delta}{n}\sum_{k=1}^nf(T+\frac{k\delta}{n})$由周期性 $S_n(x)=\frac{\delta}{n}\sum_{k=1}^nf(-T+\frac{k\delta}{n})$由定积分的定义， $\displaystyle \lim_{n\to\infty}S_n=\int_T^{T+\delta}{f(x)dx}$，若按照后一式子的写法，也可看做在分划 $\Delta_n:-T=x_0^{(n)}<x_1^{(n)}=-T+\frac{\delta}{n}<\cdots<x_{n-1}^{(n)}=-T+\frac{(n-1)\delta}{n}<x_n^{(n)}=-T+\delta$上的一个黎曼和，因此，由定积分的定义，有 $\displaystyle\lim_{n\to\infty}S_n=\int_{-T}^{-T+\delta}f(x)dx$，这就证得了 $\displaystyle \int_{-T}^{-T+\delta}{f(x)dx}=\int_{T}^{T+\delta}{f(x)dx}$，于是： $\begin{aligned} \int_{-T}^{T}{f(x)dx}=\int_{-T}^{-T+\delta}{f(x)dx}+\int_{-T+\delta}^{T+\delta}{f(x)dx}+\int_{T+\delta}^T{f(x)dx}=\\ \int_{-T}^{-T+\delta}{f(x)dx}+\int_{-T+\delta}^{T+\delta}{f(x)dx}-\int_T^{T+\delta}{f(x)dx}=\int_{-T+\delta}^{T+\delta}{f(x)dx} \end{aligned}$

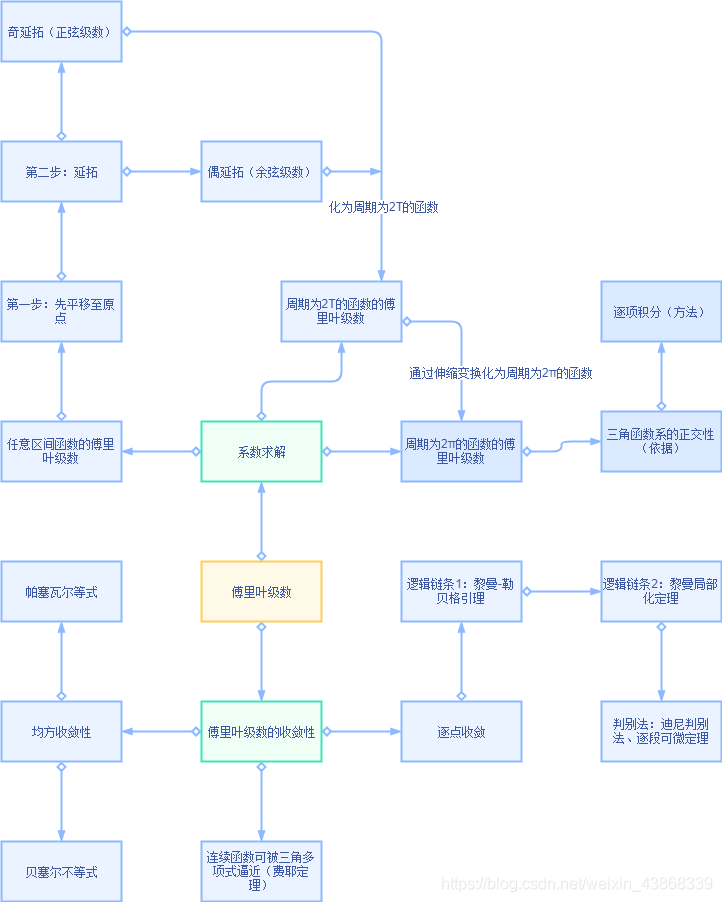
也就是说，实际上，我们任意选一个长度为 $2\pi$的区间进行积分，都是可以求出傅里叶级数的。对于 $[-\pi,\pi)$或 $[0,2\pi)$上的可积函数，我们可以通过 $\underline{延拓}$的方式将其延拓为周期为 $2\pi$的周期函数，同样可以求解傅里叶级数。下面给出若干求解傅里叶级数的例子。来展示求傅里叶级数的一般步骤。
例12.1 求 $f(x)=\pi-x,x\in[-\pi,\pi)$的傅里叶级数

解：
首先，进行延拓，延拓为周期为 $2\pi$的周期函数。
再求傅里叶系数： $\int_{-\pi}^\pi{(\pi-x)dx}=\pi x-\frac{x^2}{2}|_{-\pi}^\pi=2\pi,a_0=\pi$ $\int_{-\pi}^\pi{(\pi-x)cos(nx)dx}=0,a_n=0,n=1,2,\cdots$ $\begin{aligned} \int_{-\pi}^\pi{(\pi-x)sin(nx)dx}=-\int_{-\pi}^\pi{xsin(nx)dx}=\frac{1}{n}x\cos(nx)|_{-\pi}^\pi-\frac{1}{n}\int_{-\pi}^\pi{\cos(nx)dx}\\=\frac{2\pi (-1)^n}{n},b_n=\frac{2(-1)^n}{n},n=1,2,\cdots \end{aligned}$因此， $\displaystyle f(x) \sim \pi+2\sum_{n=1}^\infty{\frac{(-1)^n}{n}\sin(nx)}$

这是比较实用的一个例子，后面求一些特殊的级数时可以用到。
例12.2 求 $f(x)=x^{2k-1},x\in[-\pi,\pi)$的傅里叶级数

解：
求傅里叶系数:首先，对 $k=1,2,\cdots$，由奇偶性，傅里叶级数只有正弦项，设 $f_k(x)=x^{2k-1}$对应 $\sin(nx)$项的系数为 $b^{(k)}_n$，则 $\begin{aligned} b^{(k+1)}_n=\frac{1}{\pi}\int_{-\pi}^\pi{x^{2k+1}\sin(nx)dx}\\=-\frac{1}{n\pi}x^{2k+1}\cos(nx)|_{-\pi}^\pi+\frac{2k+1}{n\pi}\int_{-\pi}^\pi{x^{2k}\cos(nx)dx}\\ =-\frac{2^(-1)^n\pi^{2k}}{n}+\frac{2k+1}{n\pi}\int_{-\pi}^\pi{x^{2k}\cos(nx)dx}\\=-\frac{2(-1)^n\pi^{2k}}{n}+\frac{2k+1}{n^2\pi}x^{2k}\sin(nx)|_{-\pi}^\pi-\frac{2k(2k+1)}{n^2\pi}\int_{-\pi}^\pi{x^{2k-1}sin(nx)dx}\\ =-\frac{2(-1)^n\pi^{2k}}{n}-\frac{2k(2k+1)}{n^2}b_n^{(k)} \end{aligned}$这样我们得到一个递推式 $b^{(k+1)}_n=-\frac{2(-1)^n\pi^{2k}}{n}-\frac{2k(2k+1)}{n^2}b_n^{(k)}$这样，我们只要求出 $f(X)=x$的傅里叶级数，就可以顺着递推式得到其他的傅里叶级数而不需要再重复进行积分。而 $b_n^{(1)}=\frac{1}{\pi}\int_{-\pi}^\pi{x\sin(nx)dx}=-\frac{2(-1)^n}{n}$再由递推式，就可以得到 $\begin{cases} b_n^{(2)}=-\frac{2(-1)^n\pi^2}{n}+\frac{12(-1)^n}{n^3}\\ b_n^{(3)}=-\frac{2(-1)^n\pi^4}{n}+\frac{40(-1)^n\pi^2}{n^3}-\frac{240(-1)^n}{n^5} \end{cases}$于是就可以求出所有的傅里叶系数。

例12.3 求 $f(x)=x^{2k},x\in[-\pi,\pi]$的傅里叶系数

解：
类似于上例的做法，所有的 $\sin$项的系数均为0，而 $a_0^{(k)}=\frac{1}{2\pi}\int_{-\pi}^\pi{x^{2k}dx}=\frac{\pi^{2k}}{2(2k+1)}$ $a_n^{(k+1)}=\frac{4(k+1)(-1)^n\pi^{2k-2}}{n^2}-\frac{2(k+1)(2k+1)}{n^2}a^{(k)}_n$ $a_n^{(1)}=-\frac{4(-1)^n}{n^2}$其他项依此类推

任意区间上的函数的傅里叶级数

现在我们来考虑周期为 $2T$的函数 $f(x)$，实际上，只需要一个简单的变换 $g(x)=f(\frac{T}{\pi}x)$，即可得到周期为 $2\pi$的函数 $g(x)$，其傅里叶级数为 $a_0=\frac{1}{2\pi}\int_{-\pi}^\pi{f(\frac{T}{\pi}x)dx}=\frac{1}{2T}\int_{-T}^T{f(x)dx}$ $a_n=\frac{1}{\pi}\int_{-\pi}^\pi{f(\frac{T}{\pi})\cos(nx)dx}=\frac{1}{T}\int_{-T}^T{f(x)\cos(\frac{n\pi x}{T})dx}$ $b_n=\frac{1}{\pi}\int_{-\pi}^\pi{f(\frac{T}{\pi})\sin(nx)dx}=\frac{1}{T}\int_{-T}^T{f(x)\sin(\frac{n\pi x}{T})dx}$得到 $f(\frac{T}{\pi}x)\sim a_0+\sum_{n=1}^\infty{(a_n\cos(nx)+b_n\sin(nx))}$再作变量替换 $u=\frac{Tx}{\pi}$，得到 $f(u)\sim a_0+\sum_{n=1}^\infty{(a_n\cos(\frac{n\pi u}{T})+b_n\sin(\frac{n\pi u}{T}))}$看到这种形式，不难看出，实际上，这就是换了另一组函数系 $1,\sin(\frac{\pi x}{T}),\cos(\frac{\pi x}{T}),\sin(\frac{2\pi x}{T}),\cos(\frac{2\pi x}{T}),\cdots$再重复上一节的理论就可以得到任意周期的周期函数的傅里叶级数，形式和上面是相同的。若 $f(x)$是区间 $[a,b)$上的 函数，做平移变换 $g(x)=f(x-a)$，将其变换为 $[0,T)$上的函数，其中 $T=b-a$。接下来，我们有两种延拓方式，将其延拓为 $[-T,T)$上的函数，一种是奇延拓（正弦级数），一种是偶延拓（余弦级数），顾名思义，即是延拓为奇函数还是延拓为偶函数的区别。延拓之后，再延拓为周期为 $2T$的函数，再求解其傅里叶级数即可，这是一般函数的延拓方式。下面举几个例子说明延拓的过程。
例12.4 求下列周期为 $2\pi$的函数的正弦级数和余弦级数：
$f(x)=\sin{x},0\le x\le \pi$;

解：
首先进行奇延拓得到正弦级数，实际上，奇延拓之后 $f(x)=\sin{x},x\in[-\pi,\pi]$，其傅里叶级数即为 $f(x)\sim \sin{x}$。
再进行偶延拓得到余弦级数，当 $x\in[-\pi,0)$时， $f(x)=f(-x)=-\sin{x}$，则 $b_n=0,n=1,2,\cdots$，则 $a_0=\frac{1}{\pi}\int_{0}^\pi{\sin{x}dx}=-\frac{1}{\pi}\cos{x}|_0^\pi=\frac{2}{\pi}$ $a_n=\frac{2}{\pi}\int_0^\pi{\sin{x}\cos{nx}dx}= \frac{(-1)^n+1}{\pi(n+1)}-\frac{1}{\pi}\int_0^\pi{\sin(n-1)xdx}$由上式， $n$为奇数时， $a_n=0$， $n=2k$时， $a_n=-\frac{4}{\pi(2k-1)(2k+1)}$。从而 $f(x)\sim \frac{2}{\pi}-\frac{4}{\pi}\sum_{n=1}^\infty\frac{\cos{(2nx)}}{4n^2-1}$

例12.5 求下列周期为 $T>0$的函数的傅里叶级数：
$f(x)=x,0\le x < T$

解：
需要注意的是，周期的一半是 $\frac{T}{2}$，计算傅里叶系数时要谨慎。 $a_0=\frac{1}{T}\int_0^T{xdx}=\frac{T}{2}$ $a_n=\frac{2}{T}\int_0^T{x\cos(\frac{2n\pi x}{T})dx}=0$ $b_n=\frac{2}{T}\int_0^T{x\sin(\frac{2n\pi x}{T})dx}=-\frac{T}{n\pi}$因此 $f(x)\sim \frac{T}{2}-\frac{T}{\pi}\sum_{n=1}^\infty\frac{1}{n}\sin{(\frac{2n\pi x}{T})}$

傅里叶级数的逐点收敛

傅里叶级数部分和的表达式

接下来我们要研究的问题是：波浪号能够改为等号。与幂级数相比，傅里叶级数的部分和有其解析表达式：假设 $f(x)$以 $2\pi$为周期 $f(x)\sim a_0+\sum_{n=1}^\infty{(a_n\cos{nx}+b_n\sin{nx})}$其中，部分和为 $\begin{aligned} S_n(x)=a_0+\sum_{k=1}^{n}{(a_k\cos{kx}+b_k\sin{kx})}\\ =\frac{1}{2\pi}\int_{-\pi}^\pi{f(u)du}+\frac{1}{\pi}\sum_{k=1}^n{\int_{-\pi}^\pi{f(u)(\cos{ku}.\cos{kx}+\sin{ku}.\sin{kx})}}\\ =\frac{1}{\pi}\int_{-\pi}^\pi{f(u)(\frac{1}{2}+\sum_{k=1}^n{\cos{k(u-x)}})dx} \end{aligned}$我们来推导如下的一个公式 $(\frac{1}{2}+\sum_{k=1}^n{\cos{kx}})\sin{\frac{x}{2}}\\ =\frac{1}{2}\sin{\frac{x}{2}}+\frac{1}{2}\sum_{k=1}^n(\sin{\frac{1+2k}{2}x}-\sin{\frac{2k-1}{2}x})\\ =\frac{1}{2}\sin{\frac{2n+1}{2}x}$因此 $\frac{1}{2}+\sum_{k=1}^n{\cos{kx}}=\frac{\sin{\frac{2n+1}{2}x}}{2\sin{\frac{x}{2}}}$因此 $S_n(x)=\frac{1}{\pi}\int_{-\pi}^\pi{f(u)\frac{\sin{\frac{2n+1}{2}(u-x)}}{2\sin{\frac{u-x}{2}}}du}$做变换 $t=u-x$ $S_n(x)=\frac{1}{\pi}\int_{-\pi-x}^{\pi-x}{f(t+x)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dx}=\frac{1}{\pi}\int_{-\pi}^\pi{f(t+x)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dx}$做变换 $u=-t$ $\int_{-\pi}^0{f(t+x)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}=\int_0^{\pi}{f(x-t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$因此 $S_n(x)=\frac{1}{\pi}\int_0^\pi{[f(x+t)+f(x-t)]\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$现在，我们令 $f(x)=1$，此时 $S_n(x)=1$，这时， $\underline{傅里叶级数是可以划等号的}$，此时 $\frac{1}{\pi}\int_0^\pi{\frac{\sin{(n+\frac{1}{2})t}}{\sin\frac{t}{2}}dt}=1$现在，给定实数 $S$，我们要验证 $S_n(x)-S$是否收敛到0 $S_n(x)-S=\frac{1}{\pi}\int_0^\pi{[f(x+t)+f(x-t)-2S]\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$令 $\phi(t)=f(x+t)+f(x-t)-2S$，此时 $S_n(x)-S=\frac{1}{\pi}\int_0^\pi{\phi(t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$

黎曼局部化定理

本节要证明的是一个非常令人诧异的事实：傅里叶级数的收敛性只与 $f(x)$在某点的附近的性质有关，这从表面上看是得不出这个结论的。首先，傅里叶系数的表达式为 $\begin{cases} a_0=\frac{1}{2\pi}\int_{-\pi}^\pi{f(x)dx}\\ a_n=\frac{1}{\pi}\int_{-\pi}^\pi{f(x)\cos{(nx)}dx}&n=1,2,\cdots\\ b_n=\frac{1}{\pi}\int_{-\pi}^\pi{f(x)\sin{(nx)}dx}&n=1,2,\cdots \end{cases}$那么很自然， $f(x)$的傅里叶系数与 $f(x)$在 $[-\pi,\pi]$上的整体性质有关，下面要证明的一点是： $f(x)$在某点 $x_0$的性质，只与 $f(x)$在任意邻域 $(x_0-\delta,x_0+\delta)$上局部性质有关，就是所谓的黎曼局部化。实际上，我们不改变 $f(x)$在任意邻域 $(x_0-\delta,x_0+\delta)$上的值，改变其他区域的值，所得傅里叶系数可能大不相同，但是在 $x_0$局部，收敛性是一致的，这从表面上看是得不出了这个结论的。下面我们将要证明这个事实。\
我们这里假定 $f(x)$在 $[-\pi,\pi]$上 $\underline{黎曼可积}$，或者虽然有有限个瑕点，但是 $|f(x)|$的瑕积分是收敛的，称为 $\underline{绝对可积}$。下面我们给出一个重要的定理。

定理12.2（黎曼-勒贝格引理） $f(x)$在 $[a,b]$上黎曼可积或绝对可积，则 $\lim_{p\to+\infty}\int_a^b{f(x)\sin{(px)}dx}=0$ $\lim_{p\to+\infty}\int_a^b{f(x)\cos{(px)}dx}=0$

证：
仅证明前一个等式，后一个等式的证明是类似的。我们分两种情况证明：
第一种情况：若 $f(x)$在 $[a,b]$上黎曼可积，对任意的 $\varepsilon>0$，取一分划 $\delta:a=x_0<x_1<\cdots<x_n=n$,其中 $\omega_k$为 $f(x)$在 $[x_{k-1},x_k]$上的振幅， $m_k$为 $f(x)$在 $[x_{k-1},x_k]$上的下确界。要求该分划满足 $\sum_{k=1}^n{\omega_k \Delta x_k}<\frac{\varepsilon}{2}$由 $\int_a^b{f(x)\sin{(px)}dx}=\sum_{k=1}^n{\int_{x_{k-1}}^{x_k}{(f(x)-m_k)\sin(px)dx}}+\sum_{k=1}^n{m_k\int_{x_{k-1}}^{x_k}{\sin(px)dx}}$由于 $|\int_{x_{k-1}}^{x_k}{\sin(px)dx}|=|\frac{\cos{(px_{k-1})}-\cos{(px_k)}}{p}|\le \frac{2}{p}$ $|\int_a^b{f(x)\sin{(px)}dx}|\le \sum_{k=1}^n{\omega_k \Delta x_k} + \frac{2\sum_{k=1}^n{|m_k|}}{p}$当 $\displaystyle p>\frac{4\sum_{k=1}^n{|m_k|}}{\varepsilon}$时, $\displaystyle|\int_a^b{f(x)\sin{(px)}dx}|<\varepsilon$。
当 $f(x)$在 $[a,b]$上绝对可积时，假设 $a$是 $f(x)$的唯一的瑕点，对任意的 $\varepsilon>0$，存在 $\delta>0$，使得 $\displaystyle \int_{a}^{a+\delta}{|f(x)|}<\frac{\varepsilon}{2}$，取定 $\delta$，存在 $M>0$， $p>M$时， $|\int_{a+\delta}^b{f(x)\sin{(px)}dx}|<\frac{\varepsilon}{2}$此时 $\begin{aligned} |\int_a^b{f(x)\sin{(px)}dx}|\le |\int_a^{a+\delta}{f(x)\sin{(px)}dx}|+|\int_{a+\delta}^b{f(x)\sin{(px)}dx}| \\< \int_a^{a+\delta}{{|f(x)|}dx} + \frac{\varepsilon}{2} <\varepsilon \end{aligned}$有限个瑕点的情况可以通过分割区间证得

前面我们已经求得了 $S_n(x)-S=\frac{1}{\pi}\int_0^\pi{\phi(t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$其中 $\phi(t)=f(x+t)+f(x-t)-2S$,对 $\delta>0$，在区间 $[\delta,\pi]$上， $\frac{1}{2\sin{\frac{t}{2}}}$有界连续。若 $f(x)$黎曼可积或绝对可积，此时, $\phi(t)$在 $[\delta,\pi]$上也黎曼可积或绝对可积，由黎曼-勒贝格引理 $\lim_{n\to\infty}{ \frac{1}{\pi}\int_\delta^\pi{\phi(t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt} }=0$从而， $S_n-S$是否趋于0，取决于 $\displaystyle \frac{1}{\pi}\int_0^\delta{\phi(t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$是否趋于0，而这只与 $f(t)$在 $x$附近的性质有关系。

傅里叶级数收敛性定理的证明

现在我们来讨论傅里叶级数的收敛性问题。我们首先，需要将 $2\sin{\frac{t}{2}}$替换成 $t$，实际上， $\int_0^\delta{\phi(t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}-\int_0^\delta{\frac{\phi(t)}{t}\sin{(n+\frac{1}{2})t}dt} =\int_0^\delta{\phi(t)\frac{t-2\sin{\frac{t}{2}}}{2t\sin{\frac{t}{2}}}\sin{(n+\frac{1}{2})t}dt}$由于 $\lim_{t\to 0}{\frac{t-2\sin{\frac{t}{2}}}{2t\sin{\frac{t}{2}}}} =\lim_{t\to 0}{\frac{t-2\sin{\frac{t}{2}}}{t^2}} =\lim_{t\to 0}{\frac{1-\cos{\frac{t}{2}}}{2t}} =0$因此，函数 $\frac{t-2\sin{\frac{t}{2}}}{2t\sin{\frac{t}{2}}}$在 $(-\infty,+\infty)$上都连续， $\phi(t)$黎曼可积或绝对可积，由黎曼勒贝格引理 $\lim_{n\to\infty}{ \int_0^\delta{\phi(t)\frac{t-2\sin{\frac{t}{2}}}{2t\sin{\frac{t}{2}}}\sin{(n+\frac{1}{2})t}dt} }=0$这说明了 $\displaystyle \int_0^\delta{\phi(t)\frac{\sin{(n+\frac{1}{2})t}}{2\sin{\frac{t}{2}}}dt}$和 $\displaystyle \int_0^\delta{\frac{\phi(t)}{t}\sin{(n+\frac{1}{2})t}dt}$同敛散且极限相同。于是，可以很容易的就得到如下结论

定理12.3 (迪尼判别法) 如果 $\frac{\phi(t)}{t}$在 $[0,\delta]$上黎曼可积或绝对可积，则 $\lim_{n\to\infty}{S_n(x)}=S$

我们可以借助瑕积分的比较判别法来对傅里叶级数的收敛性进行判定。下一个问题是， $S$该如何选择？实际上，如果 $f(t)$在 $x$处连续，令 $S=f(x)$，此时 $\phi(t)=\frac{f(x-t)+f(x+t)-2f(x)}{t}$如果 $f(t)$在 $x$处不连续，但左右极限都存在，则可以令 $S=\frac{f(x+0)+f(x-0)}{2}$，此时 $\phi(t)=\frac{f(x-t)-f(x-0)}{t}+\frac{f(x+t)-f(x+0)}{t}$令 $\phi^-(t)=\frac{f(x-t)-f(x-0)}{t},\phi^+(t)=\frac{f(x+t)-f(x+0)}{t}$，这类似于广义的左右导数。如果两者都绝对可积或黎曼可积，那么傅里叶级数自然收敛于 $S$，实际上，不论连续与否，只要左右极限都存在，则 $\phi(t)=\phi^+(t)+\phi^-(t)$，我们要求两者都绝对可积或黎曼可积。

定理12.4 (利普希茨判别法) $f(x)$是以 $2\pi$为周期的函数，并且在 $[-\pi,\pi]$上只有有限个第一类间断点。若对于 $x\in [-\pi,\pi]$，存在 $M_1,M_2>0$及 $\alpha_1,\alpha_2 >0$，使得对任意的 $t>0$ $|f(x+t)-f(x)|\le M_1t^{\alpha_1}$ $|f(x-t)-f(x)|\le M_2t^{\alpha_2}$则 $f(x)$的傅里叶级数在 $x$处收敛于 $S=\frac{f(x+0)+f(x-0)}{2}$

证：
$|\phi^+(t)|\le M_1 t^{\alpha_1 - 1}$ $|\phi^-(t)|\le M_2 t^{\alpha_2 - 1}$由比较判别法 $\phi^+(t),\phi^-(t)$都绝对可积或黎曼可积，从而 $\phi(t)$绝对可积或黎曼可积

下面我们引入逐段可微的概念，所谓逐段可微，即满足：
(1) $f(x)$在 $[a,b]$上只有有限个第一类间断点 $a=x_0\le x_1<x_2<\cdots<x_{n-1} \le b=x_n$
(2)在 $(x_{k-1},x_k)$上， $f(x)$可微
(3)在 $x_k$上，两个极限 $\displaystyle \lim_{t\to 0^+}{\frac{f(x_k+t)-f(x_k+0)}{t}},\lim_{t\to 0^+}{\frac{f(x_k-t)-f(x_k-0)}{t}}$都存在
就有如下的收敛定理：

定理12.5 $f(x)$是以 $2\pi$为周期的函数，在 $[-\pi,\pi]$上逐段可微，则若 $f(x)\sim a_0+\sum_{n=1}^\infty{(a_n\cos(nx)+b_n\sin(nx))}$则 $a_0+\sum_{n=1}^\infty{(a_n\cos(nx)+b_n\sin(nx))=\frac{f(x-0)+f(x+0)}{2}}$

例12.6 计算级数 $\displaystyle \sum_{n=1}^\infty{\frac{1}{n^2}}, \sum_{n=1}^\infty{\frac{(-1)^n}{n^2}}, \sum_{n=1}^\infty{\frac{1}{n^4}}, \sum_{n=1}^\infty{\frac{(-1)^2}{n^4}}$

解：
前面我们已经求出了 $x^2,x^4(x\in[-\pi,\pi])$的傅里叶级数，分别是： $x^2\sim\frac{\pi^2}{3}+\sum_{n=1}^\infty(\frac{4(-1)^n}{n^2})\cos{(nx)}$ $x^4\sim\frac{\pi^4}{5}+\sum_{n=1}^\infty(\frac{8\pi^2(-1)^n}{n^2}-\frac{48(-1)^n}{n^4})\cos{(nx)}$由于这两个函数在延拓之后在全空间连续，并且逐段可微，因此 $x^2=\frac{\pi^2}{3}+\sum_{n=1}^\infty(\frac{4(-1)^n}{n^2})\cos{(nx)}$ $x^4=\frac{\pi^4}{5}+\sum_{n=1}^\infty(\frac{8\pi^2(-1)^n}{n^2}-\frac{48(-1)^n}{n^4})\cos{(nx)}$令 $x=0$，有 $0=\frac{\pi^2}{3}+4\sum_{n=1}^\infty{\frac{(-1)^n}{n^2}}$从而 $\displaystyle \sum_{n=1}^\infty{\frac{(-1)^n}{n^2}}=-\frac{\pi^2}{12}$，令 $x=\pi$，得 $\pi^2=\frac{\pi^2}{3}+4\sum_{n=1}^\infty{\frac{1}{n^2}}$从而 $\displaystyle \sum_{n=1}^\infty{\frac{1}{n^2}}=\frac{\pi^2}{6}$，令 $x=0$，有 $0=\frac{\pi^4}{5}+8\sum_{n=1}^\infty{\frac{(-1)^n}{n^2}}-48\sum_{n=1}^\infty{\frac{(-1)^n}{n^4}}$将 $\displaystyle \sum_{n=1}^\infty{\frac{(-1)^n}{n^2}}=-\frac{\pi^2}{12}$代入，得到 $\displaystyle \sum_{n=1}^\infty{\frac{(-1)^n}{n^4}}=-\frac{7\pi^4}{720}$，令 $x=\pi$，得到 $\pi^4=\frac{\pi^4}{5}+8\sum_{n=1}^\infty{\frac{1}{n^2}}-48\sum_{n=1}^\infty{\frac{1}{n^4}}$将 $\displaystyle \sum_{n=1}^\infty{\frac{1}{n^2}}=\frac{\pi^2}{6}$代入，得到 $\displaystyle \sum_{n=1}^\infty{\frac{1}{n^4}}=\frac{\pi^4}{90}$

例12.7 求 $f(x)=e^x,x\in(-\pi,\pi)$的傅里叶级数，并借此求解级数 $\displaystyle \sum_{n=1}^\infty{\frac{1}{1+n^2}}$

解：
先求解傅里叶级数，得到 $f(x)\sim \frac{e^\pi-e^{-\pi}}{2\pi}+\frac{e^\pi-e^{-\pi}}{\pi}\sum_{n=1}^\infty\frac{(-1)^n}{n^2+1}[\cos{(nx)}-n\sin{(nx)}]$ $f(x)$在 $[-\pi,\pi]$上逐段可微，因此 $\frac{e^\pi-e^{-\pi}}{2\pi}+\frac{e^\pi-e^{-\pi}}{\pi}\sum_{n=1}^\infty\frac{(-1)^n}{n^2+1}[\cos{(nx)}-n\sin{(nx)}]=\begin{cases} e^x&-\pi<x<\pi\\ \frac{e^\pi+e^{-\pi}}{2}&x=\pi \end{cases}$令 $x=\pi$，从而得到 $\frac{e^\pi+e^{-\pi}}{2}=\frac{e^\pi-e^{-\pi}}{2\pi}+\frac{e^\pi-e^{-\pi}}{\pi}\sum_{n=1}^\infty{\frac{1}{n^2+1}}$因此， $\displaystyle \sum_{n=1}^\infty{\frac{1}{n^2+1}} =\frac{\pi}{2}\frac{e^\pi+e^{-\pi}}{e^\pi-e^{-\pi}}-\frac{1}{2}$

例12.8 $f(x)=\cos{\alpha x},x\in (-\pi,\pi)$，其中 $\alpha>0$，且不为整数，求 $f(x)$的傅里叶级数，同时证明：当 $z \neq k\pi,k=0,\pm 1,\pm 2,\cdots$时，有 $\frac{1}{\sin{z}}=\frac{1}{z}+\sum_{n=1}^\infty\frac{2z(-1)^n}{z^2-n^2\pi^2}$ $\frac{\cos{z}}{\sin{z}}=\frac{1}{z}+\sum_{n=1}^\infty\frac{2z}{z^2-n^2\pi^2}$

解：
首先求解傅里叶级数，求得傅里叶级数为 $f(x)\sim \frac{\sin{(\alpha \pi)}}{\alpha \pi} +2\frac{\alpha \sin{(\alpha \pi)}}{\pi}\sum_{n=1}^\infty\frac{(-1)^n}{\alpha^2-n^2}\cos{(nx)}$首先令 $x=0$，得到 $1=\frac{\sin{\alpha \pi}}{\pi}[\frac{1}{\alpha}+\sum_{n=1}^\infty \frac{2\alpha(-1)^n}{\alpha^2-n^2}]$令 $z=\alpha\pi$，代入就得到 $\frac{1}{\sin{z}}=\frac{1}{z}+\sum_{n=1}^\infty\frac{2z(-1)^n}{z^2-n^2\pi^2}$令 $x=\pi$，得到 $\cos{\alpha \pi}=\frac{\sin{\alpha \pi}}{\pi}[\frac{1}{\alpha}+\sum_{n=1}^\infty \frac{2\alpha}{\alpha^2-n^2}]$令 $z=\alpha\pi$，代入就得到 $\frac{\cos{z}}{\sin{z}}=\frac{1}{z}+\sum_{n=1}^\infty\frac{2z}{z^2-n^2\pi^2}$

傅里叶级数的其他收敛性

一致收敛性

在前面我们证明了，只要 $\displaystyle \lim_{n\to\infty}{a_n}=a$，则 $\displaystyle \lim_{n\to\infty}\frac{a_1+a_2+\cdots+a_n}{n}=a$，反之不成立，说明算数平均序列比原序列有更好的收敛性。傅里叶级数也是如此，对于周期为 $2\pi$的连续函数 $f(x)$ $f(x)\sim a_0+\sum_{n=1}^\infty{(a_n\cos{(nx)}+b_n\sin{(nx)})}$前面已经推导出 $S_n(x)=a_0+\sum_{k=1}^n{(a_k\cos{(kx)}+b_k\sin(nx))}\\=\frac{1}{\pi}\int_{-\pi}^\pi{ f(x+t)\frac{ \sin(n+\frac{1}{2})t } { 2\sin\frac{t}{2} }dt }$令 $K_n(x)=\frac{S_0(x)+S_1(x)+\cdots+S_n(x)}{n+1}\\=\frac{1}{(n+1)\pi}\int_{-\pi}^\pi{ f(x+t)\frac{ \sum_{k=0}^n{\sin(k+\frac{1}{2})t} }{ 2\sin(\frac{t}{2}) }dt }$而 $\sin(\frac{t}{2})\sum_{k=0}^n{\sin(k+\frac{1}{2})t}=\frac{1}{2}\sum_{k=0}^n(\cos(kt)-\cos(k+1)t) \\=\frac{1-\cos(n+1)t}{2}=\sin^2\frac{(n+1)t}{2}$因此 $K_n(x)=\frac{1}{(n+1)\pi}\int_{-\pi}^\pi{ f(x+t)\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }$令 $f(x)=1$， $K_n(x)=1$，因此 $\frac{1}{(n+1)\pi}\int_{-\pi}^\pi{ \frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }=1$ $K_n(x)-f(x)=\frac{1}{(n+1)\pi}\int_{-\pi}^\pi{ [f(x+t)-f(x)]\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }$作积分变换，得到 $K_n(x)-f(x)=\frac{1}{(n+1)\pi}\int_{-\pi}^\pi{ [f(x+t)-f(x)]\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }\\=\frac{1}{(n+1)\pi}\int_0^\pi{ [f(x+t)+f(x-t)-2f(x)]\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }$下面我们证明以下的定理

定理12.6 $f(x)$是以 $2\pi$为周期的连续函数，并且 $f(x)\sim a_0+\sum_{n=1}^\infty(a_n\cos(nx)+b_n\sin(nx))$令 $S_n(x)=a_0+\sum_{k=1}^n{(a_k\cos{(kx)}+b_k\sin(nx))}$, $K_n(x)=\frac{S_0(x)+S_1(x)+\cdots+S_n(x)}{n+1}$，则 $\{K_n(x)\}$一致收敛到 $f(x)$

证：
由于 $f(x)$以 $2\pi$为周期且连续，因此 $f(x)$在 $(-\infty,\infty)$上一致连续。 $\forall \varepsilon >0$， $\exists \delta>0$，当 $|x_1-x_2|<\delta$时，有 $|f(x_1)-f(x_2)| < \frac{\varepsilon}{4}$，则 $\frac{1}{(n+1)\pi}\int_0^\delta{ [f(x+t)+f(x-t)-2f(x)]\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }\\\le \frac{1}{(n+1)\pi}\int_0^\delta{ [|f(x+t)-f(x)|+|f(x-t)-f(x)|]\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt }\\ \le\frac{\varepsilon}{2}\frac{1}{(n+1)\pi}\int_0^\delta\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt \le\frac{\varepsilon}{2}\frac{1}{(n+1)\pi}\int_{-\pi}^\pi\frac{ \sin^2\frac{(n+1)t}{2} }{ 2\sin^2(\frac{t}{2}) }dt=\frac{\varepsilon}{2}$作估计 $|\frac {\sin\frac{(n+1)t}{2}} {2(n+1)\sin\frac{t}{2}}|\le \frac {\frac{(n+1)t}{2}} {2(n+1)\sin\frac{t}{2}}=\frac{t}{4\sin{\frac{t}{2}}}$在 $[\delta,\pi]$上，令 $\phi(t)=f(x+t)+f(x-t)-2f(x)$，由于 $f(x)$是以 $2\pi$为周期的函数， $f(x)$有界，设 $f(x)\le M$，则 $|\phi(t)|\le 4M$，则 $\left|\frac{1}{(n+1)\pi}\int_\delta^\pi\phi(t)\frac{\sin^2\frac{(n+1)t}{2}}{2\sin^2\frac{t}{2}}dt\right|\le \frac{2M}{\pi}\int_\delta^\pi\frac{t}{\sin^2\frac{t}{2}}\sin\frac{(n+1)t}{2}dt$由于 $\frac{t}{\sin^2\frac{t}{2}}$在 $[\delta,\pi]$上连续，由黎曼勒贝格引理，存在 $N$， $n\ge N$时，就有 $\int_\delta^\pi\frac{t}{\sin^2\frac{t}{2}}\sin\frac{(n+1)t}{2}dt<\frac{\pi\varepsilon}{4M}$此时就有 $\displaystyle \left|\frac{1}{(n+1)\pi}\int_\delta^\pi\phi(t)\frac{\sin^2\frac{(n+1)t}{2}}{2\sin^2\frac{t}{2}}dt\right|<\frac{\varepsilon}{2}$，因此，对任意的 $x\in R$， $n\ge N$时，都有 $|K_n(x)-f(x)|\le \left|\frac{1}{(n+1)\pi}\int_0^\delta\phi(t)\frac{\sin^2\frac{(n+1)t}{2}}{2\sin^2\frac{t}{2}}dt\right|\\+\left|\frac{1}{(n+1)\pi}\int_\delta^\pi\phi(t)\frac{\sin^2\frac{(n+1)t}{2}}{2\sin^2\frac{t}{2}}dt\right| <\varepsilon$

注意到 $K_n(x)$是一个次数不超过 $n$的三角多项式， $K_n(x)$一致收敛到 $f(x)$，可以理解为用一系列三角多项式逼近 $f(x)$，于是就有

推论12.1 $f(x)$是以 $2\pi$为周期的连续函数，则 $f(x)$在 $(-\infty,\infty)$上可被三角多项式逼近

推论12.2 $f(x)$是以 $2\pi$为周期的连续函数，若其傅里叶系数全为0，则 $f(x)$恒为0

证：由于 $f(x)$是以 $2\pi$为周期的连续函数，且傅里叶系数全为0，则 $\forall x \in R$, $K_n(x)=0$，而 $\displaystyle\lim_{n\to\infty}K_n(x)=f(x)=0$

均方收敛

现在我们考虑以 $2\pi$为周期的函数 $f(x)$，如果 $f(x)$在 $[-\pi,\pi]$上黎曼可积， $f^2(x)$在 $[-\pi,\pi]$上也黎曼可积，若 $f(x)$在 $[-\pi,\pi]$上绝对可积，我们要求 $f^2(x)$在 $[-\pi,\pi]$上也收敛，这两种情况我们统称为 $\underline{平方可积}$。如果定义两个函数之间的内积为 $\displaystyle(f,g)=\int_{-\pi}^\pi f(x)g(x)dx$，两个函数的距离定义为 $\sqrt{(f-g,f-g)}$。现在，我们想要寻找一个 $n$次三角多项式 $S_n(x)=a_0^*+\sum_{k=1}^n(a_k^*\cos(kx)+b_k^*\sin(kx))$使得 $f(x)$与 $S_n(x)$的距离最短，那么系数应当怎么定呢？实际上 $(f(x)-S_n(x),f(x)-S_n(x))\\=(f(x),f(x))-2(f(x),S_n(x))+(S_n(x),S_n(x))$在上式中 $(f(x),f(x))=\int_{-\pi}^\pi{f^2(x)dx}$ $(f(x),S_n(x))=\pi\sum_{k=1}^n(a_k^*a_k+b_k^*b_k)+2\pi a_0^*a_0$ $(S_n(x),S_n(x))=2\pi a_0^{*2}+\pi\sum_{k=1}^n(a_n^{*2}+b_n^{*2})$于是 $(f-S_n,f-S_n)=2\pi(a_0^{*2}-2a_0^*a_0)+ \\\pi\sum_{k=1}^n[(a_k^{*2}-2a_k^*a_k)+(b_k^{*2}-2b_k^*b_k)]+\int_{-\pi}^\pi f^2(x)dx$很容易看出，当 $a_k^*=a_k,k=0,1,\cdots,n$， $b_k^*=b^k,k=1,\cdots,n$时， $(f-S_n,f-S_n)$最小，此时 $(f-S_n,f-S_n)=-2\pi a_0^2-\pi \sum_{k=1}^n(a_k^2+b_k^2)+\int_{-\pi}^\pi f^2(x)dx\ge 0$就得到不等式 $\frac{1}{\pi}\int_{-\pi}^\pi f^2(x)dx\ge 2a_0^2+\sum_{k=1}^n(a_k^2+b_k^2)$并且这对任意的 $n$都成立，这说明级数 $\displaystyle 2a_0^2+\sum_{n=1}^\infty(a_n^2+b_n^2)$绝对收敛，并且 $2a_0^2+\sum_{n=1}^\infty(a_n^2+b_n^2) \le \frac{1}{\pi}\int_{-\pi}^\pi f^2(x)dx$
定理12.7(Bassel不等式) 若绝对可积函数 $f(x)$以 $2\pi$为周期，且在 $[-\pi,\pi]$上平方可积， $f(x)\sim a_0+\sum_{n=1}^\infty{(a_n\cos(nx)+b_n\sin(nx))}$则级数 $\displaystyle 2a_0^2+\sum_{n=1}^\infty(a_n^2+b_n^2)$绝对收敛，并且成立不等式： $2a_0^2+\sum_{n=1}^\infty(a_n^2+b_n^2) \le \frac{1}{\pi}\int_{-\pi}^\pi f^2(x)dx$
接下来的问题是：这个不等式能否划上等号呢？答案是，我们先放宽条件来考察这个问题。如果 $f(x)$是以 $2\pi$为周期的连续函数，则存在三角多项式 $T(x)$，使得对任意的 $\varepsilon>0$，对任意的 $x$，都有 $\left| f(x) - T(x) \right|<\sqrt{\frac{\varepsilon}{2}}$从而 $\frac{1}{\pi}\int_{-\pi}^\pi[f(x)-T(x)]^2dx<\varepsilon$假设 $T(x)$是 $n_0$次三角多项式，则 $\frac{1}{\pi}\int_{-\pi}^\pi[f(x)-S_{n_0}(x)]^2dx \le \frac{1}{\pi}\int_{-\pi}^\pi[f(x)-T(x)]^2dx<\varepsilon$当 $n\ge n_0$时，都有 $\frac{1}{\pi}\int_{-\pi}^\pi[f(x)-S_{n}(x)]^2dx \le \frac{1}{\pi}\int_{-\pi}^\pi[f(x)-S_{n_0}(x)]^2dx <\varepsilon$从而 $\lim_{n\to\infty}\frac{1}{\pi}\int_{-\pi}^\pi[f(x)-S_{n}(x)]^2dx=0$从而不等式可以改成等式，假设 $f(x)$以 $2\pi$为周期，并且在 $[-\pi,\pi]$上可积，我们想先用一个连续函数逼近可积函数，最容易想到的连续函数是分段线性函数，由于 $f(x)$在 $[-\pi,\pi]$上可积，对任意的 $\varepsilon>0$，由于 $f(x)$有界，设 $|f(x)|\le M$，取 $[-\pi,\pi]$的一个分划 $\Delta:-\pi=x_0<x_1<\cdots<x_n=\pi$，其中 $\omega_k$为 $f(x)$在 $[x_{k-1},x_k]$上的振幅 $(k=1,\cdots,n)$，要求该分划满足 $\sum_{k=1}^n\omega_k\Delta x_k <\frac{\pi \varepsilon^2}{2M}$连接 $(x_{k-1},f(x_{k-1}))$和 $(x_k,f(x_k))$再进行周期延拓，得到分段线性并以 $2\pi$为周期的连续函数 $g(x)$，当 $x\in [x_{k-1},x_{k}]$时，存在 $\lambda\in[0,1]$，使得 $g(x)=\lambda f(x_{k-1}) + (1-\lambda)f(x_k)$从而 $\left|g(x)-f(x)\right|\le \lambda \left|f(x_{k-1})-f(x)\right|+(1-\lambda)\left|f(x_{k-1})-f(x)\right|\le\omega_k$同理，设 $|f(x)|\le M$，则 $|g(x)|\le M$，则 $|g(x)-f(x)|\le 2M$，于是 $\frac{1}{\pi}\int_{-\pi}^\pi[f(x)-g(x)]^2dx\le\frac{2M}{\pi}\int_{-\pi}^\pi|f(x)-g(x)|dx \\=\frac{2M}{\pi}\sum_{k=1}^n\int_{x_{k-1}}^{x_k}|f(x)-g(x)|dx \le\frac{2M}{\pi}\sum_{k=1}^n\omega_k\Delta x_k<\varepsilon$存在三角多项式 $T(x)$，满足 $\frac{1}{\pi}\int_{-\pi}^\pi[g(x)-T(x)]^2dx<\varepsilon$有 $\frac{1}{\pi} \int_{-\pi}^\pi[f(x)-T(x)]^2dx \le \frac{2}{\pi} \int_{-\pi}^\pi[f(x)-g(x)]^2dx\\+ \frac{2}{\pi} \int_{-\pi}^\pi[g(x)-T(x)]^2dx <4\varepsilon$用类似的方法可以证明，贝塞尔不等式也可以取等号，若 $f(x)$有有限个瑕点，绝对可积且平方可积时，假设 $f(x)$唯一的瑕点是 $x\in(-\pi,\pi)$， $\forall \varepsilon>0$，存在 $\delta>0$，使得 $\int_{c-\delta}^{c+\delta}f^2(x)dx<\frac{\varepsilon}{4}$这里设 $c+\delta<\pi,c-\delta>-\pi$，构造以 $2\pi$为周期的函数 $\overline{f}(x)=\begin{cases} 0&c-\delta<x<c+\delta\\ f(x)&-\pi\le x\le c-\delta 或 c+\delta\le x\le\pi \end{cases}$ $\overline{f}(x)$在 $[-\pi,\pi]$上可积，存在三角多项式 $T(x)$，满足 $\frac{1}{\pi}\int_{-\pi}^\pi[\overline{f}(x)-T(x)]^2dx<\frac{\varepsilon}{4}$于是 $\frac{1}{\pi}\int_{-\pi}^\pi[f(x)-T(x)]^2dx \le \frac{2}{\pi}\int_{-\pi}^\pi[f(x)-\overline{f}(x)]^2dx\\+\frac{2}{\pi}\int_{-\pi}^\pi[T(x)-\overline{f}(x)]^2dx<\varepsilon$类似地，就容易得到

定理12.8(帕萨瓦尔等式) $f(x)$是以 $2\pi$为周期的函数，若 $f(x)$在 $[-\pi,\pi]$上可积或绝对可积且平方可积 $f(x)\sim a_0+\sum_{n=1}^\infty(a_n\cos(nx)+b_n\sin(nx))$则成立帕萨瓦尔等式 $2a_0^2+\sum_{n=1}^\infty(a_n^2+b_n^2)=\frac{1}{\pi}\int_{-\pi}^\pi f^2(x)dx$

这等价于 $\displaystyle \lim_{n\to\infty} \int_{-\pi}^\pi[f(x)-S_n(x)]^2dx=0$，称为 $S_n(x)$平方收敛到 $f(x)$。