动态规划基本概念
动态规划(DP:Dynamic Programming):是一种重要的程序的设计手段,其基本思想是在对一个多阶段决策的问题,按照某一顺序,根据每一步所选决策的不同会引起状态的转移,最后会在变化的状态中获取到一个决策序列。
动态规划是一种把多阶段过程转化为一系列单阶段问题,逐个求解的方法,广泛应用于生产调度,工程技术和最优控制等领域。
动态规划与分治法异同:
相同点:都是将问题划分成一些子问题,递归求解各子问题,然后合并子问题的解而得到原问题的解。
不同点: 分治法是将问题划分在相互独立的子问题,因此部分问题会被重新计算;动态规划方法分解得到的子问题往往不互相独立,而是互相重叠的,从而避免了大量重复计算。
举例说明
裴波那契数列的递归表达式如下所示
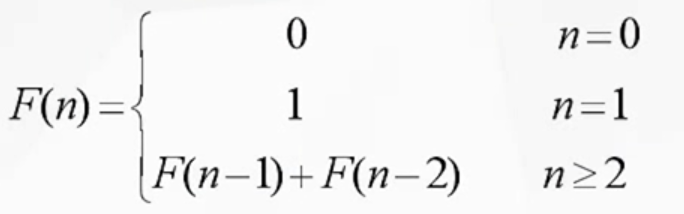
当n=5时,我们用分治法计算裴波那切数列
第一步f(5)分解成f(4)和f(3),第二步f(4)分解成f(3)和f(2),f(3)分解成f(2)和f(1),此时f(1)已经有确定的解了,无需在分解,第三步对第二步中产生的三个子问题进行进一步分解,直到无需分解为止,从求解过程可以看出,分治法把问题分解成的子问题间是相互独立的。比如对f(3)进行了两次重复计算,对f(2)进行了三次重读计算。
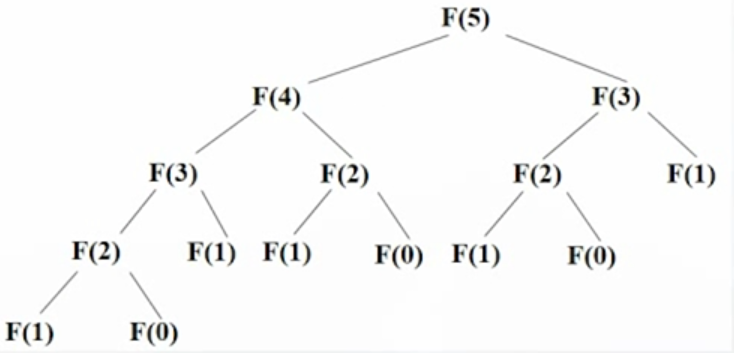
我们使用动态规划法求解裴波那契数列,通过递归的公式发现,f(n)是以计算它的两个重叠子问题f(n-1)和f(n-2)的形式来表达的,所以可以设计一张表填入n+1个f(n)的值。
动态规划法求解裴波那契数列f(9)的填表过程:
 使用前两项和作为第n项的值,不必重复计算子问题,提高了执行效率。
使用前两项和作为第n项的值,不必重复计算子问题,提高了执行效率。
具体求解步骤如下:
f(0),f(1)已知,f(2)可以由f(0),f(1)相加得到,f(3)可以由f(1),f(2)相加得到.依次类推,从求解过程中可以看到,每一步都是在上一步求解的基础上进行的。采用自底向上的策略,不必重复计算,提高了效率。
动态规划的基本要素
1、最优子结构性质
一般来说,只要该问题可以划分成规模更小的问题,并且原问题的最优解中包含了子问题的最优解,则可以考虑用动态规划解决。
分析问题是否满足最优原理(反证法)

2、子问题的重叠性质
适用于动态规划求解的问题,经分解得到的子问题往往不是相互独立,而是重复出现的,对于重复出现的子问题,只在第一次遇到时加以求解,并把答案保存起来,以后在遇到是不必重新求解。
动态规划的实质就是分治思想和解决冗余的结合。
(1)将问题实例分解为更小的,相似的子问题。
(2)存储子问题的解而避免计算重复的子问题。
动态规划步骤
(1)分析最优解的性质,并刻划其结构特性
(2)递归的定义最优质
(3)以自底向上或自顶向下的方式计算出最优质
(4)根据递归计算出最优值时得到的信息,从子问题的最优解逐步构造出整个问题的最优解。
矩阵连乘描述
给定n个矩阵{A1,A2,…,An},其中,Ai与Ai+1是可乘的,(i=1,2 ,…,n-1)。用加括号的方法表示矩阵连乘的次序,不同的计算次序计算量(乘法次数)是不同的,找出一种加括号的方法,使得矩阵连乘的次数最小。
A1是A(5*10)的方阵;
A2是A(10*100)的方阵;
A3是A(100*2)的方阵;
那么有两种加括号的方法:
1. (A1A2)A3;
2. A1(A2A3);
第一种方法的计算量:5*10*100+5*100*2=6000;
第二种方法的计算量:10*100*2+5*10*2=2100;
可以看出不同计算方法计算量差别很大。
问题分析
1、 矩阵连乘的条件:第一个矩阵的列等于第二个矩阵的行,此时两个矩阵是可乘的;
2、 多个矩阵连乘的结果矩阵,其行列等于第一个矩阵的行和最后一个矩阵的列;
3、两个矩阵相乘的计算量:
例如:A(32),B(24)
java代码
public class DynamicPlan {
/**
* 此方法用来求解矩阵连乘的最小数乘次数
*
* @param p
* 传入的要连乘的矩阵的维数信息的数组
* @return String型的矩阵的最小数层次数信息
*/
public static String matrixChain(int p[]) {
int n = p.length - 1; //为p的实际最大下标
int m[][] = new int[n + 1][n + 1];
int s[][] = new int[n + 1][n + 1];
for (int i = 1; i <= n; i++) {
m[i][i] = 0;
}
for (int r = 2; r <= n; r++) // r为当前计算的链长(子问题规模)
{
for (int i = 1; i <= n - r + 1; i++)// n-r+1为最后一个r链的前边界
{
int j = i + r - 1;// 计算前边界为r,链长为r的链的后边界
m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];// 将链ij划分为A(i) *( A[i+1:j] )
s[i][j] = i;
for (int k = i + 1; k < j; k++) {
// 将链ij划分为( A[i:k] )* (A[k+1:j])
int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
if (t < m[i][j]) {
m[i][j] = t;
s[i][j] = k;
}
}
}
}
String answer = "";
answer = answer + "此矩阵连乘所需的最小次数为:" + m[1][n] + "\n";
matrixTraceBack(1, n, s);
return answer;
}
private static void matrixTraceBack(int i, int j, int s[][]) {
if (i == j) {
return;
}
matrixTraceBack(i, s[i][j], s);
matrixTraceBack(s[i][j] + 1, j, s);
int x = s[i][j] + 1;
System.out.print("Multipy A" + i + "," + s[i][j]);
System.out.println(" and A" + x + "," + j);
}
}
