问题描述

矩阵连乘问题就是让我们找一个加括号的位置,使得加完括号之后矩阵的计算次数最小。这是一道典型的动态规划问题,而且和我们昨天讨论的题目动态规划解决多边形最优三角剖分很相似,大家可以参考一下。
题目分析
学过线性代数的朋友一定都知道矩阵相乘是有条件的,即AxB的条件是A矩阵的列数应该等于B矩阵的行数,这样两个矩阵才能相乘。
现在考虑三个矩阵的连乘运算,加括号方式会对整个计算量产生影响。现有矩阵A1,A2,A3,这三个矩阵的维度分别为10x100,100x5,5x50,按照第一种加括号的方式((A1A2)A3),3个矩阵乘积需要的数乘次数为10x100x5+10x5x50=7500.
而另一种加括号方式(A1(A2A3)),3个矩阵乘积需要的数乘次数为 100x5x50+100x50x10=75000。很明显这运算次数一下子高了10倍,所以加括号的方式对于矩阵的运算次数真的有很大的影响。
我们加括号的方法是,对于n个矩阵的连乘积,设有不同的计算次序P(n)。可以现在第k个(k=1,2,…,n-1)和第k+1个矩阵之间将原矩阵序列分为两个矩阵子序列,然后分别对这两个矩阵子序列完全加括号,最后得到的结果加括号,得到原矩阵序列的一种完全加括号方式这显然是一个递归过程。
将矩阵连乘积AiAi+1…Aj简记为A[i:j]。考察计算A[1:n]的最优计算次序。设这个计算次序在矩阵Ak(1<=k<=n)和Ak+1之间将矩阵链断开,则其相应的完全加括号方式为((A1…Ak)(Ak+1…An))。依此次序,先计算A[1:k]和A[k+1:n],再将计算结果相乘,得到A[1:n]。依此计算顺序,总计算量为A[1:k]的计算量加上A[k+1:n]的计算量,再加上A[1:k]和A[k+1:n]相乘的计算量。
这道题目之所以和多边形最优三角剖分很相似是因为他也涉及到子问题规模的不断增大以及划分方式的不断改变。既然是矩阵连乘,那么最小的子问题规模一定是2,而且我们对加括号的位置也会不断改变,最外层控制子问题大小,内层循环控制加括号位置的不断移动,从而动态规划的效果。
首先我们假设m[i][j]为矩阵从i连乘到j的最小数乘次数,即计算A[i:j]所需的最少数乘次数。不难理解,m[i][i]=0。所以m[i][j]可以递归定义如下:
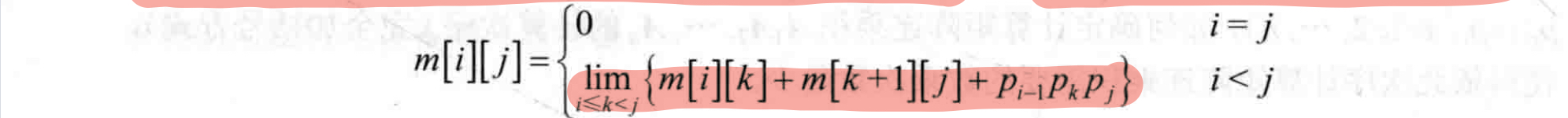
我们将对应m[i][j]断开的位置k记为s[i][j],在计算出最优值m[i][j]后可递归地由s[i][j]构造出相应的最优解。
关于pi-1pkpj的问题,我们可以通过刚才的例子来进一步解释,有矩阵A1,A2,A3,这三个矩阵的维度分别为10x100,100x5,5x50,按照第一种加括号的方式((A1A2)A3),3个矩阵乘积需要的数乘次数为10x100x5+10x5x50=7500.这里的10x100x5是怎么来的呢,我们就可以将A[i:k]与A[k+1:j]这两部分矩阵想象为矩阵A1A2,pi-1就是10,pk就是100,pj就是5.因为我们规定矩阵Ai的行数为pi-1,列数为pi,所以pi-1xpkxpj就不难理解了,大家可以根据具体的例子进行验证。
代码
#include <iostream>
using namespace std;
void MatrixChain(int *p,int n,int **m,int **s)
{
//p是用来记录矩阵的行列数
//p[i-1]表示Ai的行数,pi表示矩阵Ai的列数
for(int i = 1;i <= n;i++)
m[i][i] = 0;
for(int r = 2;r <= n;r++)
{
for(int i = 1;i <= n - r + 1;i++)
{
int j = i + r - 1;
m[i][j] = m[i+1][j] + p[i-1]*p[i]*p[j];
s[i][j] = i;//此时划分位置为i
for(int k = i + 1;k < j;k++)
{
int t = m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t > m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}总结
动态规划问题就是要划分出各种子问题,这些子问题的求法和原问题一模一样,我们可以直接利用求解好的子问题对原问题进行求最优。
