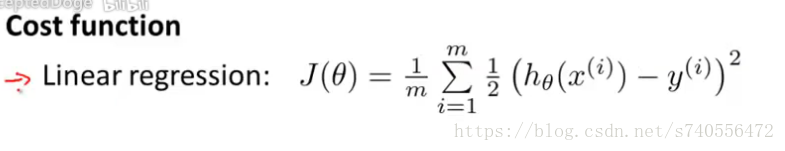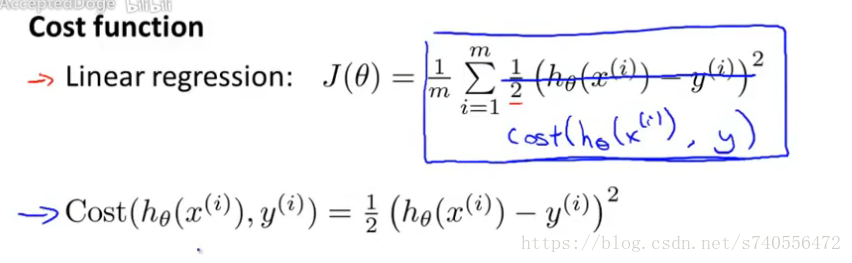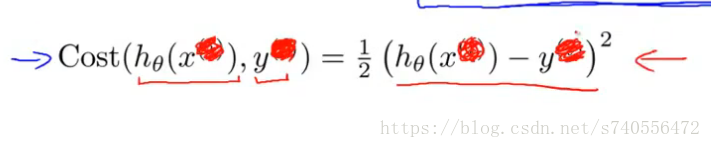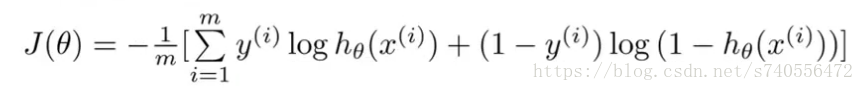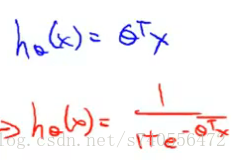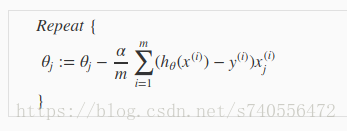Logistic Regression Model(逻辑回归模型)
Cost Function
如下所示,本章讲述了如何拟合cost参数θ:
hypothesis函数在图中复习一下,在图中我们的假设函数范围在0-1之间.
在线性回归方程中我们的代价函数如下:
现在改写一下,去掉平方,让下图蓝色字体等于平方差,实际上还是对数据集从1-m求和的公式,只不过简写了而已,如下图:
简化上面的式子,去掉上标,直接定义,Cost(hθ(x),y):其中hθ(x)代表假设函数,y代表实际函数,如下图:
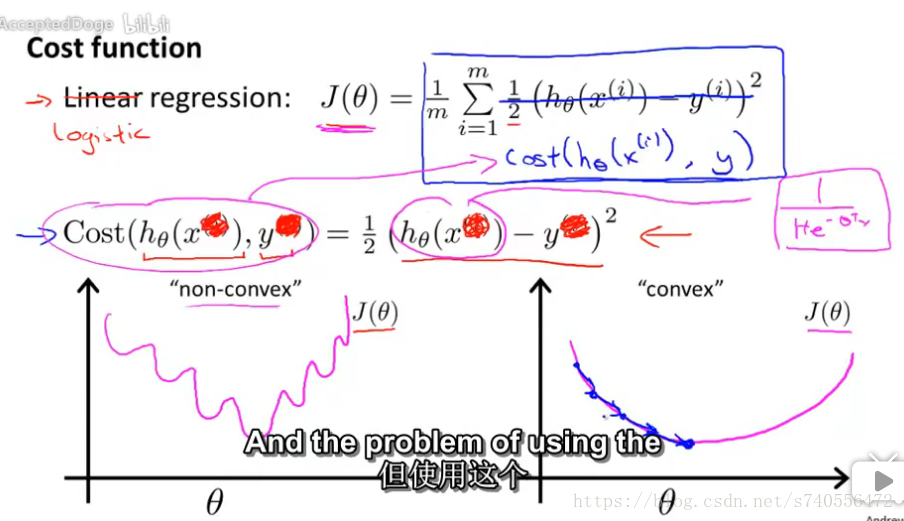
有了这个等式,我们可以把上一章中的逻辑回归的方程带入到hypothesis函数中,按照下图的粉红色线从右往左依次带入公式,最终J(θ)可以得到下图左下的那张图,其中non-convex代表的含义是非凸函数,但是问题是这样的图形来用作梯度下降会发现,不能保证它收敛到全局最小值。而下图右下侧的图形,使我们想要的convex凸函数图形,也就是J(θ)图形的理想化,这样的图形可以使梯度下降找到全局最小值。
结论:如果我们用非线性的sigmoid函数来作为假设函数回
推代价函数的话,并不能得到很好的凸函数图形。所以接下来,我们要寻找一个更好的代价函数。
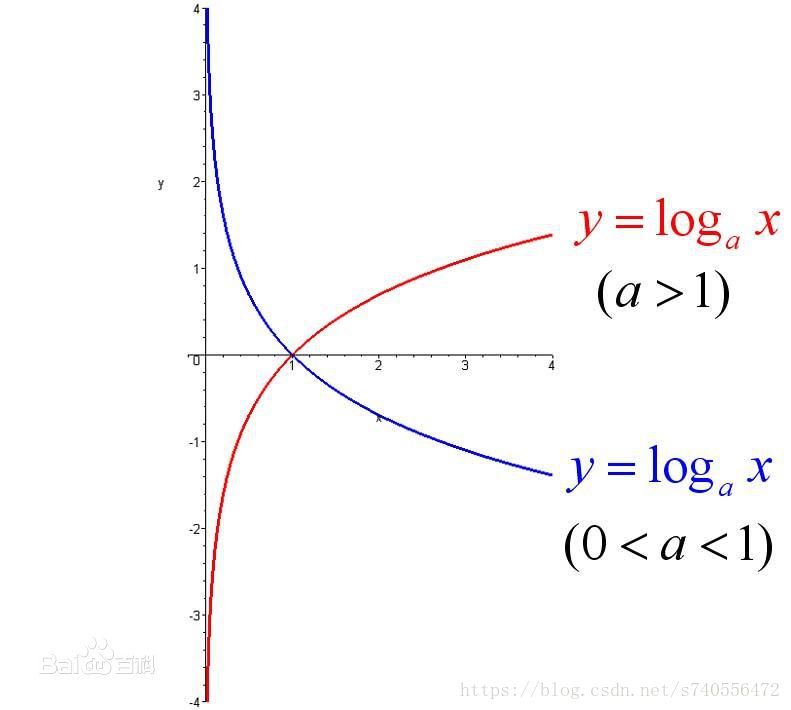
再此之前,先复习一下数学知识,log函数的图像:
于是有了下面的图:
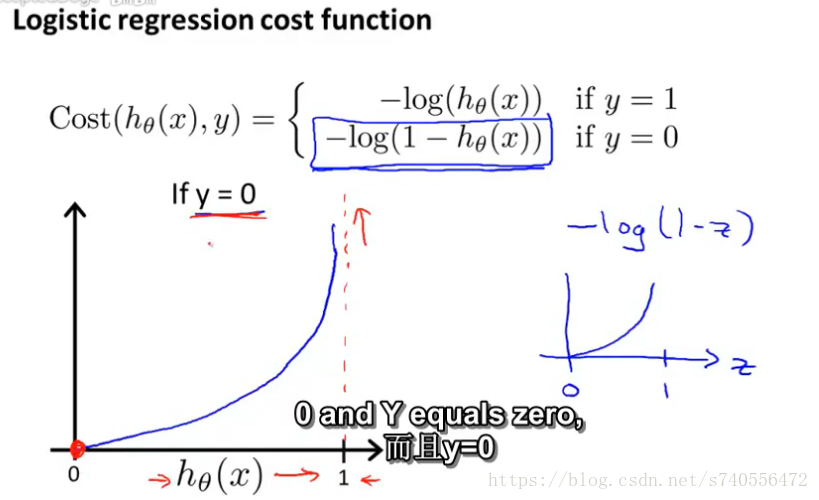
上图左下图形表示: 如果当y=1时,那么代价函数的图形对应的公式为:-log(hθ(x))。这个图的横轴是h(x)即预测值,纵轴是cost函数的值,也就是预测值和真实值的差。
这张图的右侧英文很好的解释了为什么当y=1时,式子是这样的比较好。y代表的是我们数据的真实值,h(x)代表的是预测值,当h(x)=1,我们可以从图中看到,cost=0,当代价函数等于0时,正是我们想要的结果,说明 h(x)(预测值)=y(实际值)=1。但是同理,若h(x)越是趋近0,代价函数也越趋近正无穷,误差也就越大!
这里教授同时也说到另一个问题,当假设函数的值等于0,那么y=1的概率是0。这类似于病人得恶性肿瘤的概率,就是说你的肿瘤完全不可能是恶性的,然而结果是病人的肿瘤确实是恶性的。如果出现这样的结果,我们需要狠狠的惩罚一下这个算法!
接下来看下图,当y=0时代价函数的图:
当hθ(x)趋近与1时,也就是预测的值是1时,而最终真实的y是0,则说明我们需要这个算法付出一个很大的代价!…与上面一样,因为预测出来的值违背了真实值。反过来,如果假设函数预测对了,预测的y是0,而y就是等于0,那么说代价函数在这点上应该就是等于0.
Simplified cost funciton and gradient descent
本章讲解了用梯度下降算法那来拟合出逻辑回归的参数。
Simplified cost funciton
在上面讲述了关于代价函数的表达式,分两种情况,一个是y=1,一个是y=0.而对于这种表达式,我们还有更简便的写法,如下图:
再来张机打高清图:
为什么说这个式子等于上一章说的呢,这里正向推导我是不知道怎么来的,但是教授的反向推导倒是看明白了。他解释了一下反向推导的过程:
当y=1时,我们将其带入高清机打图的公式中:可以看到后面的第二项(1-y)=0,而最终得到的结果=======Cost(hθ(x),y) = -log(hθ(x))。
当y=0时,我们将其带入高清机打图的公式中:可以看到第一项-y=0,而最终得到的结果=======Cost(hθ(x),y) = -log(1-hθ(x))。个人理解这就是逆向推导....
通过上面的写法,将2行的条件代价函数式子写成了一行。而这样写的好处是什么?视频里并木有说…但是这个式子是从统计学中的最大似然估计(Maximum Likelihood Estimate,MLE)得来的。统计学的思路是从不同的式子中有效地找出不同的参数。同时它还有一个好处,就是它是凸函数!所以这就是大部分人使用的逻辑回归代价函数。这里说一句wiki里的:在统计学中,最大似然估计,也称为最大概似估计,是用来估计一个概率模型的参数的一种方法。
接下来将得到的Cost(hθ(x),y)带回到之前说的类似线性J(θ)函数中,如下图:
我们尽量让J(θ)取得最小值,假设我们给出一个新的样本值x,用下面的式子来输出对假设的预测,假设我们的hypothesis预测的概率就是P(y=1|x;θ),这个式子的含义关于θ参数时y=1的概率。
结论:我们通过逆向推导可以很清晰的理解逻辑回归代价函数的简单版,它是通过统计学总结出来的。将Cost()函数简化后带回原式得到J(θ):
最终,我们需要关心的是如何最小化代价函数J(θ),而最小化的方法就是使用梯度下降算法。
gradient descent
利用梯度下降法重复更新θj,如下图:
a代表的是学习速率,这和线性回归时后的梯度下降是一样的,而对J(θ)进行微积分,得到的是图中蓝色字体的公式(其实就是预测误差乘上X(i)j),将其带回到原来的式子中,可以得到如下形式的写法:
再来看,如果当我们有一组θ向量时,我们用梯度的这个式子同时更新θ值,但是细细的想一下这个式子,是不是很眼熟呢?其实这个式子是跟线性回归梯度下降时,当θ=1时是一个式子!!如下图:
那么线性回归的梯度下降算法和逻辑回归的算法是同一个算法吗?来看看二者之间的区别: 最大的区别就是虽然梯度下降的表达式是一样的,但是对于hθ(x)来说,它们的定义是不同的
线性回归:hθ(x)=θ^T·X
逻辑回归:hθ(x)=1/(1+e^-(θ^T·X))
下图所示:
当我们在线性回归梯度下降时,讲述了如何监控梯度下降算法如何保证收敛(特征缩放的方法 feature scaling),同样的我们也可以将其用在逻辑回归的梯度下降中。忘记了可以看这篇博客。
特征缩放的博客需要补一下!!!之前跳过了中间Octave课程,没想到把特征缩放视频也跳过去了…第二周笔记的最后会补一下,这里mark一下。!!! 特征缩放的博客需要补一下!!!
结论:在梯度下降算法中,我们可以将逻辑回归方程的算法求导过程仿照线性回归的梯度下降一样推导。而逻辑回归方程中的J(θ)如下:
梯度公式如下:
Advanced Optimization
本节讲述高级优化算法和一些高级优化概念,使用这些方法会使我们逻辑回归算法的速度更快,能更好的解决大型的机器学习问题。
梯度下降算法:
如果我们不用梯度下降算法,其实还有其他高级算法供我们选择,而最好的方式就是调库使用。
其他的算法:
共轭梯度法(Conjugate gradient);
BFGS算法;
L-BFGS算法。
这些算法优点是不需要我们手动的选择α;速度快于梯度下降法。缺点是复杂。
所以我们只需要会使用它们,而不需要深究其中的原理。
在视频中,教授用Octave举例了fminunc函数。再次不做记录了。
本章重点:对于想快速求解大量数据的代价函数,我们可以采用调库形式的高级算法进行求解。学会调库,调库并不可耻~
展望结语
忧伤,从上一次笔记到现在已经过了小半个月了,中间各种研究java工作相关的东西,晚上回家是真的挤不出时间了….现在继续恢复正常,每天一个小视频,坚持坚持!今日打卡,滴滴滴!下一次的博客是多类分类和过拟合笔记。。。。
已经在奔往机器学习的路上——!