逻辑回归 学习笔记

逻辑回归

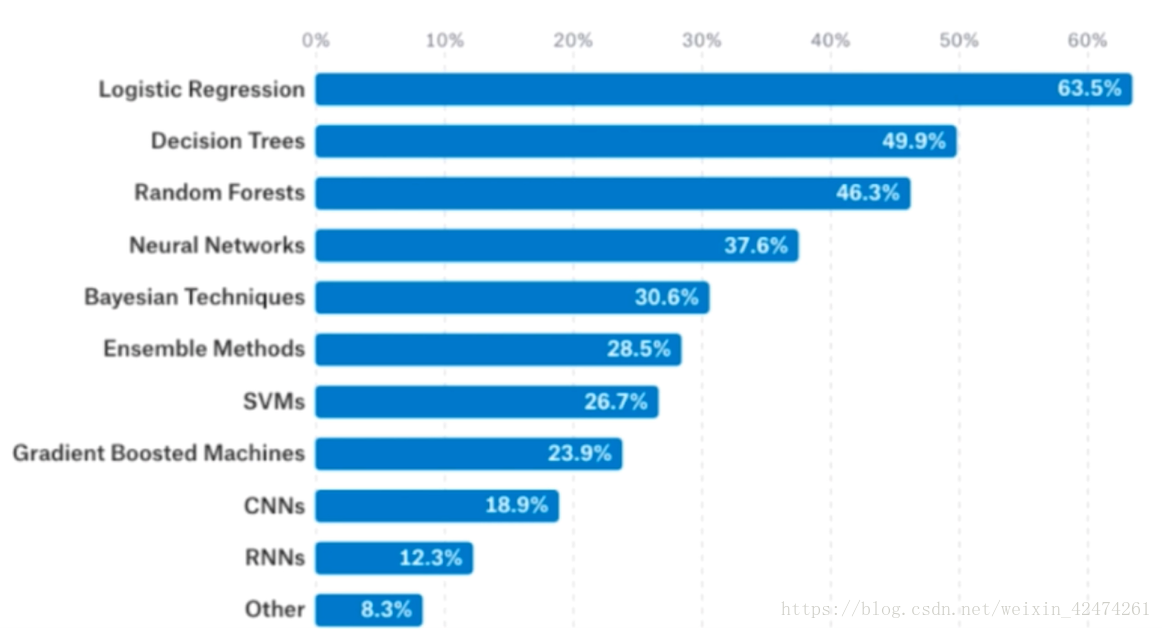
据统计，在kaggle上使用逻辑回归解决问题的比例是非常大的，并且超出第二名决策树20%多，说明逻辑回归普适性较强，而神经网络相关算法对数据的要求比较高。

什么是逻辑回归

听起来逻辑回归是一个回归算法，但是事实上它解决的却是分类问题。它的原理是将样本的特征与样本发生的概率练习起来。
$P = f(x)$
根据概率值P进行分类
$P = \begin{cases} 1 & 0.5 \leq P < 1 \\0 & 0 \leq P < 0.5 \end{cases}$
逻辑回归本身只可以解决二分类问题，可以通过改进解决多分类问题。
在线性回归中通过 $f(x)$的计算，根据样本值计算出 $y$值，表示为
$y = \Theta^T X_b$
其中 $y = f(x)$的值域在 $(-\infty,+\infty)之间，而逻辑回归取值范围在$[0, 1]之间。因此直接使用线性回归的方式来表达逻辑回归的值不太合适。
解决方案是通过 $\sigma$方法，来将 $y$的取值加以限定，那么就的到了下面的式子
$p = \sigma(\Theta^T X_b)$
我们将 $\sigma(t)$设置成这样一个函数
$\sigma(t)= \frac{1}{1+e^{-t}}$
因为这个Sigmoid函数的曲线如下图1：

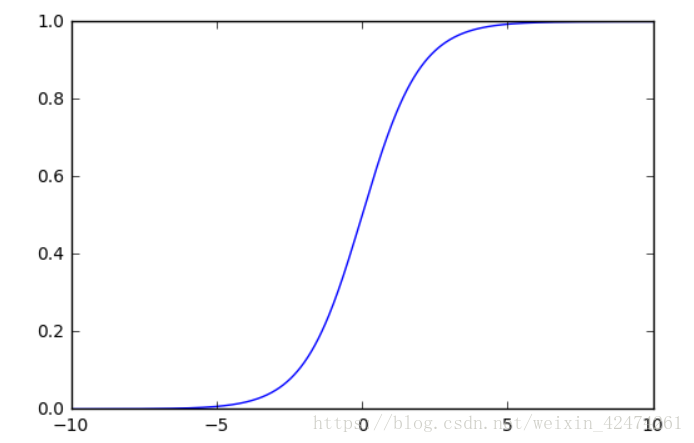
通过在 $(0,0)$处建立直角坐标系，可以分析得出，当 $x\rightarrow-\infty$时， $y$值无限趋近于0，当 $x\rightarrow\infty$时， $y$值无限趋近于1。
则事件发生的概率可以表示为：
$\sigma(t)= \frac{1}{1+e^{-\Theta^T X_b}}$
例子：病人数据预测肿瘤是良性还是恶性
每来一组新的数据，通过Sigmoid函数的计算把 $y$值来与0.5比较，当概率值 $y > 0.5$时，我们就预测患者肿瘤是恶性的，如果 $y < 0.5$，我们就预测患者的肿瘤是良性的。
问题：
如何找到参数theta，使用这样的方式，可以最大程度获得样本数据X对应的分类输出y

逻辑回归的损失函数

首先它的损失函数趋势如下
$cost = \begin{cases} 如果y=1,p越小，cost越大 \\如果y=0,p越大，cost越大\end{cases}$
则可以找到满足该趋势的如下函数
$cost = \begin{cases}-\log(p) & if & y = 1 \\-\log(1-p)& if &y=0 \end{cases}$

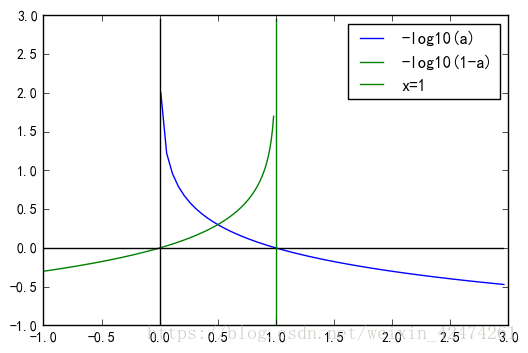
将cost损失函数整合到一起，用一个式子来表达，可得到
$cost = -yln(p)-(1-y)ln(1-p)$
m个样本求平均
$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m}{y^{(i)}ln(p^{(i)})+(1-y^{(i)})ln(1-p^{(i)})}$
$p^{(i)}=\sigma(\Theta X_b^{(i)})= \frac{1}{1+e^{-\Theta X_b^{(i)}}}$
接下来的任务是找到一个 $\theta$使得损失函数 $J(\theta)$，没有公式解，只能用梯度下降法求解。
通过求导得到 $ln(\sigma(t))^{'} = 1- \sigma(t)$ $ln(\sigma(1-t))^{'} = -\sigma(t)$
最终，得到损失函数对某个特征值求导得到的结果
$\frac{J(\theta)}{\theta_j}= \frac{1}{m}\sum_{i=1}^m(\widehat{y}^{(i)} - \sigma(X_b^{(i)}\theta))X_j^{(i)}$
$\nabla J(\theta) = \left\{\begin{matrix} \sum_{i=1}^m(\widehat{y}^{(i)} - y^{(i)}) X_0^{i}\\ \sum_{i=1}^m(\widehat{y}^{(i)} - y^{(i)}) X_1^{i} \\ \sum_{i=1}^m(\widehat{y}^{(i)} - y^{(i)}) X_2^{i} \\ \vdots \\ \sum_{i=1}^m(\widehat{y}^{(i)} - y^{(i)}) X_n ^{i} \\ \end{matrix} \tag{1} \right\} = \frac{1}{m}\centerdot X_b^{T}\centerdot(\sigma(X_b\theta) - y)$