引言
本文介绍了决策树,它和KNN一样,也是一个非参数学习算法;决策树可以解决多分类问题,同时也可以解决回归问题。
决策树具有非常好的可解释性。
决策树
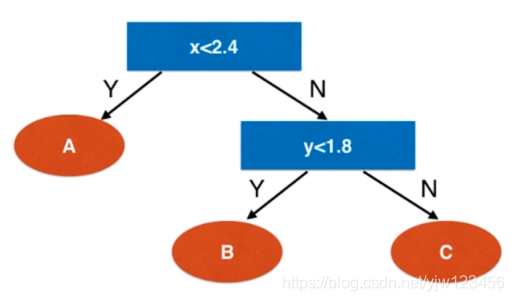
先来看下什么是决策树。决策树描述了一些规则,根据这些规则可以做出决策。比如某公司想招聘机器学习算法工程师,他们可能会先看应聘者是否在顶级会议上发表过论文,如果发表过的话则直接录用;否则看应聘者是否为研究生,如果是并且读研期间做的项目是和机器学习有关的,则录用;无关的则留待考察;若不是研究生,则看成绩是否是年纪前10,是的话则录用否则留待考察。
这样的过程就可以用决策树描述出来。
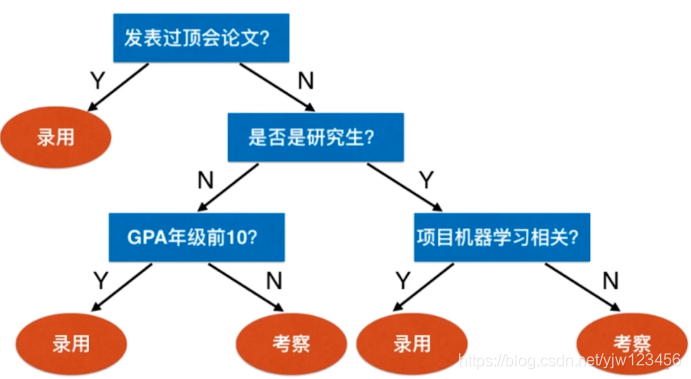
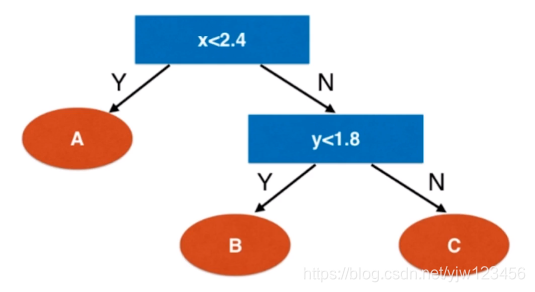
我们可以说这颗树的深度为3,因为最多通过三次判断就可以得出结论。这里是一颗二叉树,每个叶子节点就是最终的类别,而非叶子节点可以看是决策的规则。
在这个例子中,决策的时候属性都可用yes和no来回答,这里是通过文字描述。实际上很多都是具体的数值。
如果是数值,那么该如何表示呢。我们通过sklearn封装的类来看下是怎么做的,初步了解下决策树。
我们使用真实数据来演示:
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:] #只用后两个维度,方便可视化
y = iris.target
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
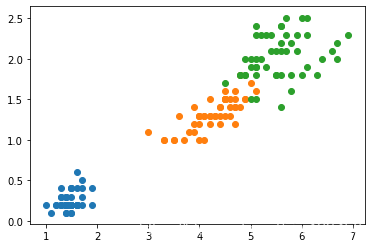
下面使用sklearn的决策树来对这个数据进行分类:
from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier(max_depth=2,criterion='entropy') #决策树最大深度
dt_clf.fit(X,y) #模型训练
使用很简单,只要实例化好类之后,调用fit方法进行训练即可。训练完了之后,我们画出决策边界。
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
plot_decision_boundary(dt_clf,axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
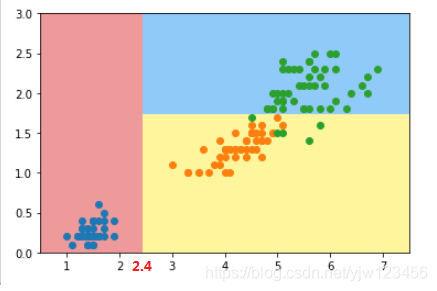
这就是决策树得到的决策边界。我们本例的数据特征都是数字特征,我们现在有两个特征,我们称横坐标为
,纵坐标为
。
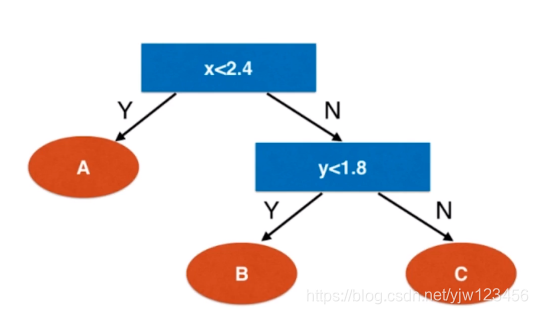
先来看横坐标,如果 ,那么可以直接分类为一类,就是红色区域,记为类别 。
否则在右侧,再来看纵坐标,是否
,是的话则分为
类,就是上面黄色区域,否则为
类,上面蓝色区域。这样就得到了决策树:
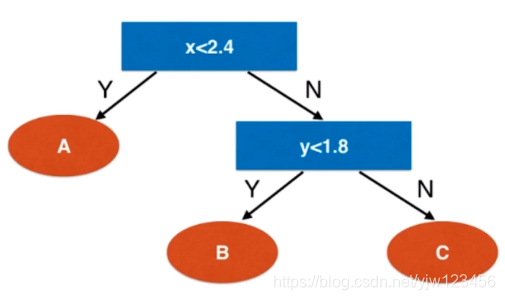
上面是我们手动画的决策树,下面我为大家介绍一种用代码画决策树的方法。
可视化决策树
我们要用到graphviz,需要先下载下来,并配置环境变量。
接下来配置环境变量
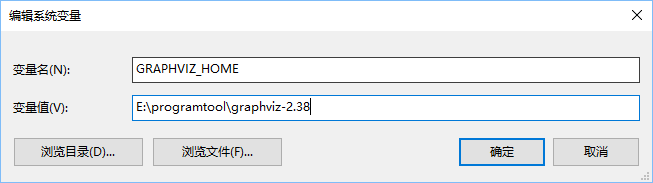
然后编辑系统Path,新增:

完了之后我们输入dot -v看是否配置成功。
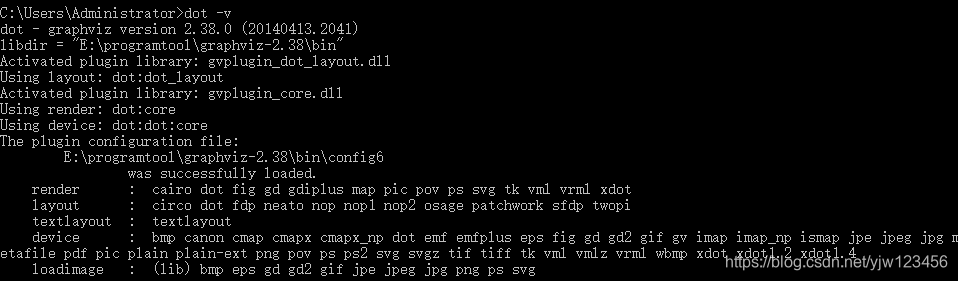
接下来还要做的一件事情是安装python模块pip install graphviz,完了之后执行下面的代码
from sklearn.tree import export_graphviz
import graphviz
export_graphviz(dt_clf, out_file="dt_clf.pdf")
with open('dt_clf.pdf') as f:
dot_graph = f.read()
graphviz.Source(dot_graph)
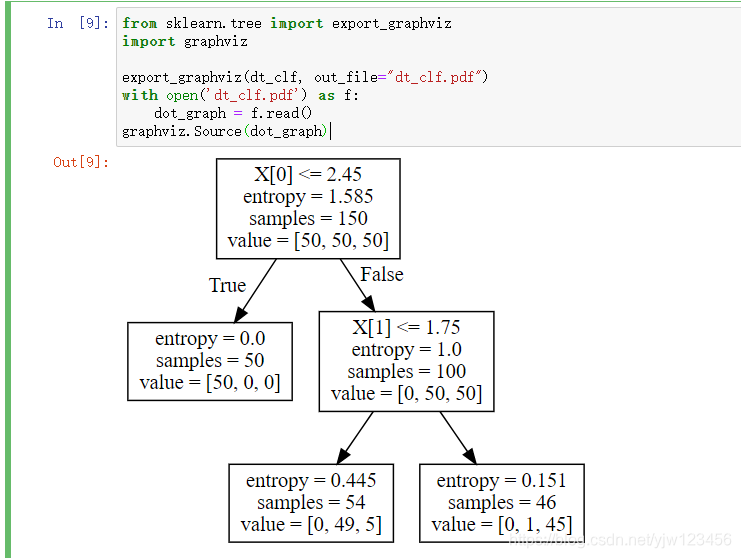
这样就可以生成一颗可视化的决策树。并且可以看到上面我们手动画的决策树中,划分维度是对的,但是划分阈值就没那么准确了。
我来解释下每个节点,entropy是每个节点的熵,samples是每个节点上的样本数,value是一个数组,样本属于每个类别的数量。
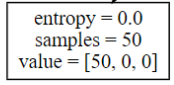
比如在这个叶子节点中,样本都集中在一个类别上,因此熵就为零。
好了,接下来我们来了解下如何构建决策树。我们可以从上图看到,每个节点,首先找到一个维度(这里是 或 ),其次找到该维度的一个阈值,以这个阈值为依据判断,并继续划分。
现在的问题是每个节点在哪个维度做划分,以及选好了维度后,该在哪个值上做划分呢。
我们先来学习信息熵的方法。
信息熵
在决策树的每个非叶子节点上都是一个判断条件,为了得到这个判断条件。我们需要得到两个信息
- 在哪个维度进行划分
- 确定维度后,在哪个值上进行划分
本节介绍信息熵的方式。什么是信息熵呢。
熵是随机变量不确定度的度量。
- 熵越大,数据的不确定性越高;
- 熵越小,数据的不确定性越低。
可以这样理解熵,熵越大,相当于粒子无规则运动越剧烈。像水加热蒸发成气体的时候,它的粒子相对比较活跃,运动的很剧烈,此时熵比较大,并且温度也较高;当水结冰的时候,粒子相对静止,熵比较小。
来看下香农提出的信息熵的公式吧:
代表一个系统中每类信息所占的比例,假如共有 类信息。因为我们的 ,因此 ,也就是每项都是小于零的,因此在外面加个负号,使得整个式子的结果是正的。注意这里的 底数是 和 都可以的。
我们还是通过例子来感受一下。假设我们的数据集中有3个类别,它们分别占了 。
那它的熵为:
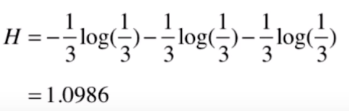
只看一组数据没什么感觉,我们再来看一组
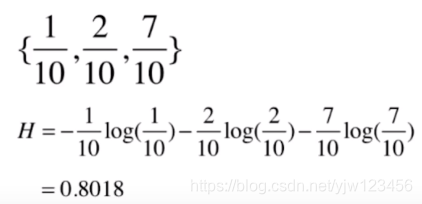
现在我们就可以比较熵的结果了,显然第二份数据的熵比第一份数据要小。怎么理解呢,第二份数据大多集中在类别3中,其占比为
,因此是比较集中(确定)的,熵较小。
我们再来看下一个极端的例子。
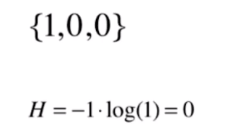
此时数据都集中在类别1中,因此数据没有不确定性,熵为0。注意这里有个约定是 。
我们以二分类问题为例,来看下这个信息熵公式的函数图像是什么样的。在二类问题中,如果一类占比为 ,那么另一类即为 。
因此,二分类问题中熵就可以写成:
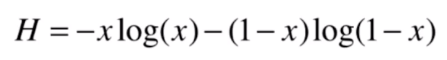
下面我们来看下这个函数图像是什么样的,看下函数图形与 的取值关系。
import numpy as np
import matplotlib.pyplot as plt
def entropy(p):
return - (p * np.log2(p) + (1-p) * np.log2(1-p))
x = np.linspace(0.01,0.99,200) #x坐标,过滤掉log0
y = entropy(x)
plt.plot(x,y)
plt.show()
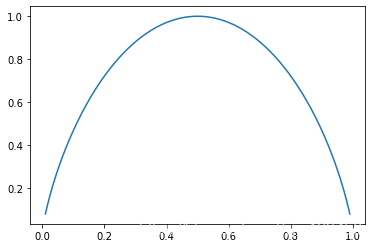
我们绘制出的图像如上,可以看到,当
趋近于
或
是,熵最小,此时因为占比越集中;当
时,熵最大,为
,此时数据集中的数据属于每个类别的概率都是50%,不确定性最大。
了解了信息熵的概念,
- 在哪个维度进行划分
- 确定维度后,在哪个值上进行划分
这两个问题就好说了,我们划分要做的事情是,划分后使得信息熵降低。也就是让整个系统变得更加确定。
极端情况下,上面每个叶子节点的上的数据都只属于
类,
类,
类时,此时整个系统的信息熵最低,低到了零。
因此在划分时,我们选择能使系统的信息熵降低程度最大的那个维度,并且在每个维度上找一个取值,使得熵降低的最大。这样我们就回答了上面两个问题。
下面我们根据这个思路来编码实现一下。
使用信息熵寻找最优划分
对于我们的决策树来说,在根节点上我们要找到一个维度和一个阈值,对根节点进行划分,使得系统整体的信息熵降低最大;继而在划分出来的两个节点可以再通过同样的方式来寻找最佳的维度和阈值。
我们通过代码来模拟一下划分的过程。
from collections import Counter
from math import log
#划分函数,针对数据X,和输出y。根据维度d的value值进行划分
def split(X,y,d,value):
left = (X[:,d] <= value) #在d维度上的值小于等于value的部分
right = (X[:,d] > value)
return X[left],X[right],y[left],y[right]
# 计算熵
def entropy(y):
#y包含数据的所有类别
counter = Counter(y)
res = 0.0
for num in counter.values():
p = num/len(y) #每个类别的占比
res += -p * log(p,2)
return res
# 寻找最佳划分
def try_split(X,y):
# 找到一组划分,使得信息熵最低
best_entropy = float('inf') #最低的信息熵
best_d,best_v = -1,-1 #最好的维度和维度上的阈值
# 寻找最好的维度和最好的阈值
for d in range(X.shape[1]): #穷举X的所有维度
sorted_index = np.argsort(X[:,d])#根据d维数据排序
# 阈值就是相邻两个样本点在维度d上中间的值
for i in range(1,len(X)): #遍历每个样本
if X[sorted_index[i-1],d] != X[sorted_index[i],d]: #如果相等的话, 它们的平均值无法分开这两个样本点,我们不要这种均值
v = (X[sorted_index[i-1],d] + X[sorted_index[i],d])/2.0 #阈值就是相邻两个样本点在维度d上中间的值
#调用split函数进行划分
X_l,X_r,y_l,y_r = split(X,y,d,v)
#计算划分后,得到的信息熵
e = entropy(y_l) + entropy(y_r)
if e < best_entropy:
best_entropy,best_d,best_v= e,d,v
return best_entropy,best_d,best_v
接下来我们针对上面介绍的数据进行一下调用:
try_split(X,y)
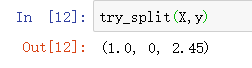
可以看到,我们对根节点的最佳划分是在第0个维度,阈值为2.45的地方。划分后,我们的信息熵变成了1。
其实计算信息熵的时候是不强调
底数的,这里用
为底的话,得到的信息熵就是
。用
为底,得到的就是

但是不管用什么为底,得到的划分都是一样的。
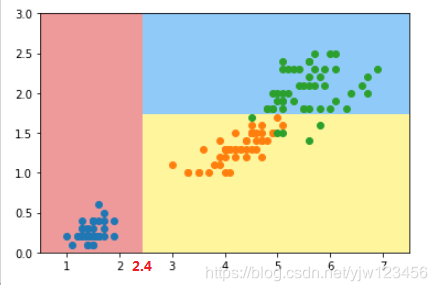
我们将这个节点与sklearn中得到的结果进行比较,可以看到上图中的位置应该是2.45(开始标错了)。结果还是一致的。
best_entropy,best_d,best_v = try_split(X,y)
X1_l,X1_r,y1_l,y1_r = split(X,y,best_d,best_v)
print(entropy(y1_l))
print(entropy(y1_r))
我们还可以保存下刚才划分的结果,并计算划分后的信息熵。


用y1_l表示第一次划分左边的类型,计算其信息熵为0。结合上图也很好理解,我们这次划分成功的把蓝点所有的数据都划分到了左边,并且里面只有蓝色样本点。因此是很集中的,没有任何不确定性。
相应的y1_r为1,就是上图红色区域的右边,包括蓝色和黄色区域部分。此时,我们还是可以进行划分的,因为熵的值比较大。
再一次调用try_split(X1_r,y1_r)。注意此时我们只需要传入划分后的右边部分。
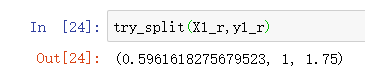
调用的结果显示,我们在第1个维度,1.75的值处进行划分,可以得到最好的信息熵。

可以看到sklearn中第二次划分也在维度1上,并且阈值也是1.75左右。
同样我们记录下第二次划分的结果。
best_entropy2,best_d2,best_v2 = try_split(X1_r,y1_r)
X2_l,X2_r,y2_l,y2_r = split(X1_r,y1_r,best_d2,best_v2)
print(entropy(y2_l))
print(entropy(y2_r))
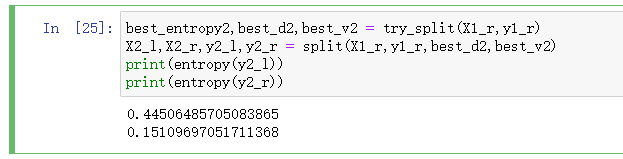
可以看到,经过这次划分后两颗子树的信息熵有所降低,但是都没有降为零。因此其实还可以向更深的方向继续进行划分。
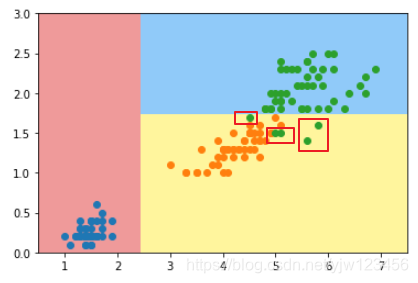
在这个划分结果中,黄色区域还有一些绿色样本点。我们通过sklearn的算法得到的划分结果也是到此为止了,为什么呢,因为我们设置了决策树深度为2,即最多只能判断2次。
其实除了信息熵这个划分指标外,常用的还有基尼系数这个指标。下面一起来学习一下。
基尼系数
它的公式比信息熵简单很多。
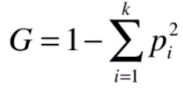
是每个类别的占比,虽然简单,但是它具有和信息熵同样的性质。我们同样以具体的例子为例:
如果3个类别所占的比例都是
的话
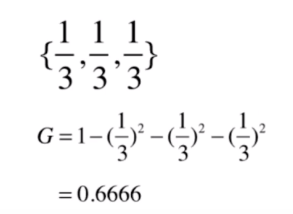
再来看第2组数据:
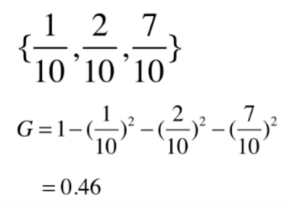
从结果可以看到,和信息熵一样,第二组数据的结果比第一组要低。
基尼信息越高说明,整体的不确定性越强。
再来看下第三组极端的情况:
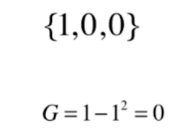
基尼系数为零也是没有任何的不确定性。
和信息熵一样,我们来看下函数图像是什么样的。在二类问题中,一类占比为 ,另一类为 。
因此,基尼系数可以写成:
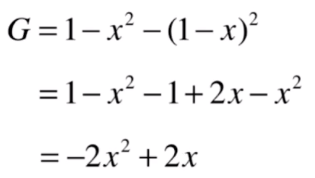
最后整理可以写成上式。
def gini(p):
return -2*p**2 +2*p
x = np.linspace(0.01,0.99,200)
y = gini(x)
plt.plot(x,y)
plt.show()
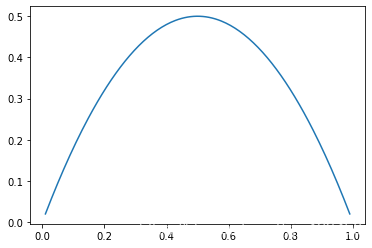
最后得到的图像和信息熵的也很像,只不过
的取值不同。如果信息熵那里,我们
的底数取自然数
,再画图看看:
import numpy as np
import matplotlib.pyplot as plt
def entropy(p):
return - (p * np.log(p) + (1-p) * np.log(1-p))
def gini(p):
return -2*p**2 +2*p
x = np.linspace(0.01,0.99,200) #x坐标,过滤掉log0
y = entropy(x)
plt.plot(x,y)
plt.show()
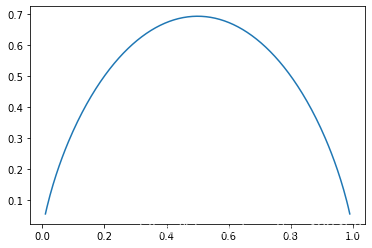
可以看到,最大值还是有点差别,但是整个形状可以说是一样的了,这就可以解释为什么在很多情况下它们是可以互换的。
又到了通过代码实现的时间了,我们看下sklearn中要怎么做:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:] #只用后两个维度,方便可视化
y = iris.target
dt_clf = DecisionTreeClassifier(max_depth=2,criterion='gini')
dt_clf.fit(X,y) #模型训练
其实很简单,只要修改criterion为gini即可。然后画出决策边界:
plot_decision_boundary(dt_clf,axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
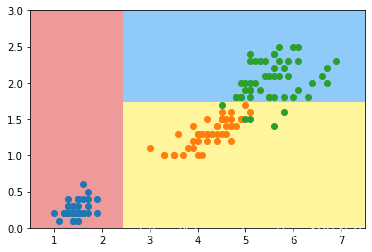
可以看到,其实绘制的结果和使用信息熵是相同的。我们再用可视化工具看一下:
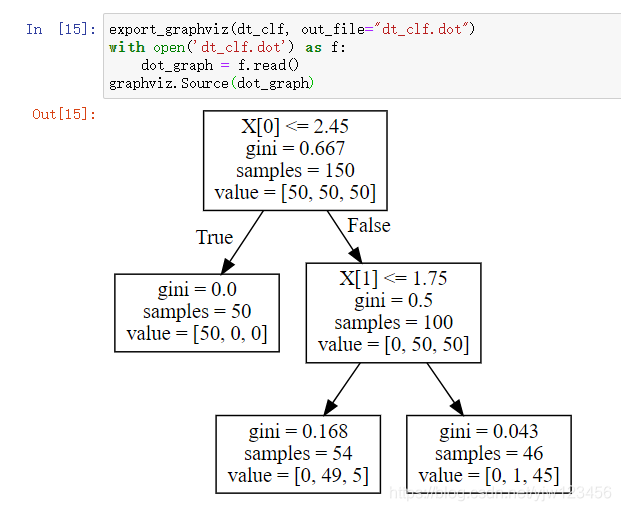
这里我修改了下输出文件的格式,看上去和信息熵的图像一样,除了中间的指标变成了gini。
和信息熵一下,我们也通过代码来实现一下。其实只要把上面代码中的指标改成基尼系数:
def gini(y):
counter = Counter(y)
length_y = len(y)
res = 1 - sum([(num/length_y)**2 for num in counter.values()])
return res
这里用python中的列表推导式来简化下代码。
from collections import Counter
from math import log
#划分函数,针对数据X,和输出y。根据维度d的value值进行划分
def split(X,y,d,value):
left = (X[:,d] <= value) #在d维度上的值小于等于value的部分
right = (X[:,d] > value)
return X[left],X[right],y[left],y[right]
# 计算基尼系数
def gini(y):
counter = Counter(y)
length_y = len(y)
res = 1 - sum([(num/length_y)**2 for num in counter.values()])
return res
# 寻找最佳划分
def try_split(X,y):
# 找到一组划分,使得基尼系数最低
best_gini= float('inf') #最低的基尼系数
best_d,best_v = -1,-1 #最好的维度和维度上的阈值
# 寻找最好的维度和最好的阈值
for d in range(X.shape[1]): #穷举X的所有维度
sorted_index = np.argsort(X[:,d])#根据d维数据排序
# 阈值就是相邻两个样本点在维度d上中间的值
for i in range(1,len(X)): #遍历每个样本
if X[sorted_index[i-1],d] != X[sorted_index[i],d]: #如果相等的话, 它们的平均值无法分开这两个样本点,我们不要这种均值
v = (X[sorted_index[i-1],d] + X[sorted_index[i],d])/2.0 #阈值就是相邻两个样本点在维度d上中间的值
#调用split函数进行划分
X_l,X_r,y_l,y_r = split(X,y,d,v)
#计算划分后,得到的信息熵
g = gini(y_l) + gini(y_r)
if g < best_gini:
best_gini,best_d,best_v= g,d,v
return best_gini,best_d,best_v
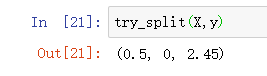
下面我们保存下划分的值:
best_gini,best_d,best_v = try_split(X,y)
X1_l,X1_r,y1_l,y1_r = split(X,y,best_d,best_v)
print(gini(y1_l))
print(gini(y1_r))
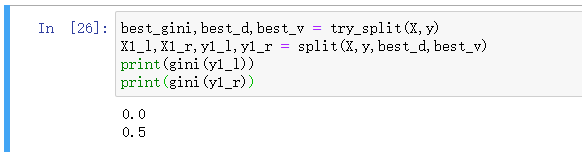
此时右子树的基尼系数不为零,我们可以继续划分一次:

说明需要在第1个维度,1.75的位置进行划分,这与我们上面得到的结果一致。基尼系数下降到了0.21。
best_gini,best_d,best_v = try_split(X,y)
X1_l,X1_r,y1_l,y1_r = split(X,y,best_d,best_v)
print(gini(y1_l))
print(gini(y1_r))
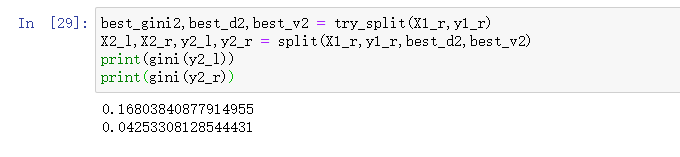
划分完了之后,基尼系数又降低了,但是还没到零,可以继续划分。
现在我们知道了信息熵和基尼系数这两种方式,那么它们有什么区别和联系呢。
- 因为信息熵的式子教复杂,因此信息熵的计算比基尼系数稍慢,sklearn中默认就为基尼系数
- 大多数情况下二者没有特别的效果区别
- 信息熵趋向于产生更加平衡的树,而基尼系数喜欢将高频类放到自己的分支上。
CART与超参数
现在我们已经了解了什么是决策树以及如何构建一颗决策树,其实上面我们实现的决策树是CART(Classification And Regression Tree)。从名字可以看到,它既可以解决分类问题,也可以解决回归问题。
主要思想就是根据某一个维度d和某一个阈值v进行二分,产生的是一颗二叉树。我们自己写的代码中就是这么做的。
sklearn中实现的决策树也是CART。其他的诸如ID3,C4.5在统计学习方法中有介绍。
我们来看下复杂度
当我们构建好了一颗决策树后,基于它进行预测的时间复杂度为
。
是样本数量。
但是由我们上面实现的算法可知,训练过程是比较耗时的,需要在每个维度上面对每个样本就行考察(n * m),树的结构是要
,因此训练一棵树的时间复杂度为
和KNN这种非参数学习算法一样,决策树算法也很容易产生过拟合,因此我们实际在创建决策树的过程中,需要对其进行剪枝,以降低复杂度,解决过拟合问题。
具体怎么剪枝呢,其实我们上面已经进行过剪枝,我们指定了最大深度max_depth,就是对它的复杂度进行一个限制,实际上就是一个剪枝手段。
除了通过max_depth之外,还有哪些方式呢,我们下面就来看一下。
还是以例子来说明,先生成一些模拟数据。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X,y = datasets.make_moons(noise=0.25,random_state=666)#设置一个较大的noise
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
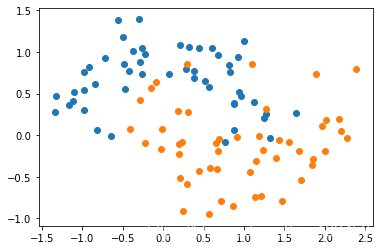
如果我们训练一颗决策树,那在这个例子中,决策边界是怎样的呢?
from sklearn.tree import DecisionTreeClassifier
dt_clf = DecisionTreeClassifier()#默认的是基尼系数 以及不限制最大深度
dt_clf.fit(X,y)
plot_decision_boundary(dt_clf,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
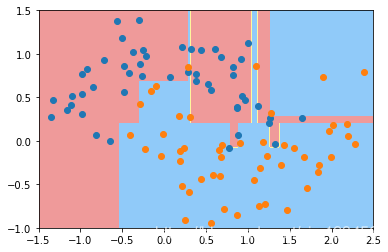
可以看到得到的决策边界是这样的,它的形状很不规则,有很多长的线条,这是过拟合导致的。
下面我们通过在构建决策树的时候传入一些参数,这些参数是如何防止过拟合的。
dt_clf2 = DecisionTreeClassifier(max_depth=2)
dt_clf2.fit(X,y)
plot_decision_boundary(dt_clf2,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
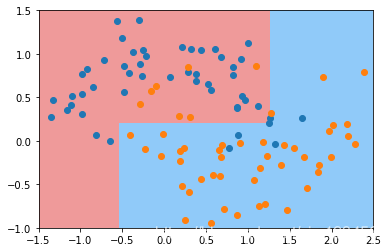
首先我们指定了决策树的最大深度,此时得到的结果是很规整的。没有很长的线条。显然没有过拟合。
但是此时很可能是欠拟合,因此还需对参数进行精细的调整。我们来看看其他参数(min_samples_split):
dt_clf3 = DecisionTreeClassifier(min_samples_split=10)#节点最少的样本数,低于该样本数的节点不再拆分
dt_clf3.fit(X,y)
plot_decision_boundary(dt_clf3,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
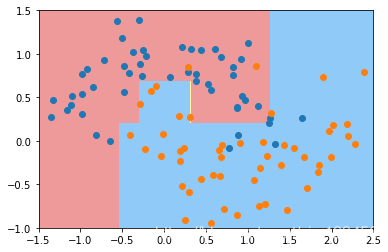
显然它的过拟合程度不高。这个值调的越高就越不容易过拟合,但是如果过高则会产生欠拟合。
还有一个参数是min_samples_leaf:
dt_clf4 = DecisionTreeClassifier(min_samples_leaf=6)#对于叶子节点来说,最少的样本数。 越小越容易过拟合
dt_clf4.fit(X,y)
plot_decision_boundary(dt_clf4,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
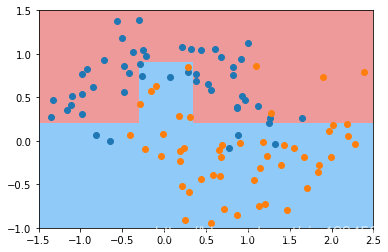
最后再来看一个参数max_leaf_nodes:
dt_clf5 = DecisionTreeClassifier(max_leaf_nodes=4)#最多有多少个叶子节点,叶子节点越多,则越复杂,越容易过拟合
dt_clf5.fit(X,y)
plot_decision_boundary(dt_clf5,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
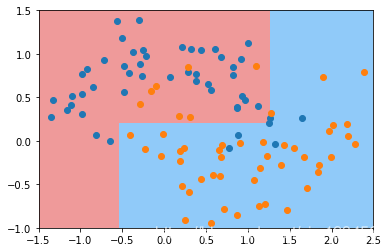
决策树解决回归问题
上面我们提到过决策树可以解决回归问题,我们现在来看一下是如何解决的。
解决的思路很简单,上面我构建的决策树中的叶子节点,通过投票最多输出类别。如果我们输出一个具体的数值,就可以解决回归问题。这个数值一般取该节点样本值的均值。
这个思路是很简单的。我们看下sklearn中要怎么做
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor #回归
boston = datasets.load_boston()
X = boston.data
y = boston.target
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=666)
dt_reg = DecisionTreeRegressor()#使用默认参数
dt_reg.fit(X_train,y_train)
dt_reg.score(X_test,y_test)
这里使用的是波斯顿房价数据,我们计算score的值为0.57,使用默认的参数得到的结果不是很理想。
如果我们计算训练数据的score:

哇,达到了最大值。说明针对我们的训练集,预测的准确率是100%的,结合测试数据来看,显然是过拟合了。
我们可以使用上小节介绍的内容来消除过拟合。
我们尝试绘制基于r2_score的学习曲线,来看下什么时候发生了过拟合
from sklearn.metrics import r2_score
#绘制学习曲线
def plot_learning_curves(model, X_train, X_test, y_train, y_test):
train_score,test_score = [], []
for m in range(1, len(X_train)): #不停的增加样本数来学习
model.fit(X_train[:m], y_train[:m])
y_train_predict = model.predict(X_train[:m])
y_test_predict = model.predict(X_test)
train_score.append(r2_score(y_train[:m],y_train_predict))
test_score.append(r2_score(y_test, y_test_predict))
plt.plot(train_score, label="train")
plt.plot(test_score, label="test")
plt.legend()
plt.show()
画图函数定义好了后,我们就来尝试下:
plot_learning_curves(dt_reg,X_train,X_test,y_train,y_test)
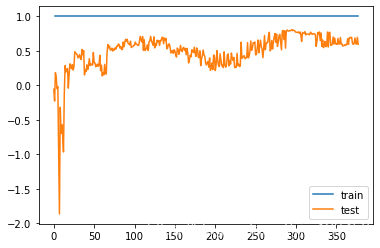
此时在训练数据上得分达到了最大值,但是在测试数据上波动的很剧烈。
我们可以尝试不同的参数来看下函数图像的不同:
plot_learning_curves(DecisionTreeRegressor(max_depth=1),X_train,X_test,y_train,y_test)
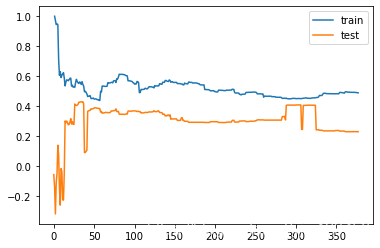
plot_learning_curves(DecisionTreeRegressor(max_depth=3),X_train,X_test,y_train,y_test)
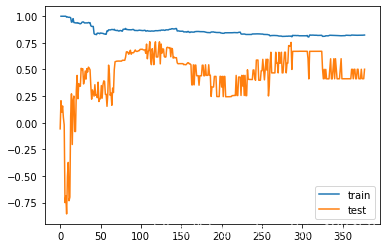
调整最大深度为3,测试集的得分明显比最大深度为1的时候要好。说明一定程度上减少了过拟合。
决策树的局限性
最后来看一下决策树的局限性。
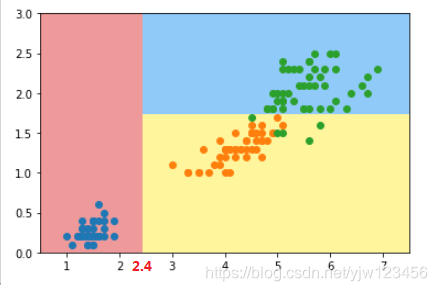
决策树的一个明显的局限性是容易过拟合。除了这点 外,我们看下产生的决策边界是要么平行于X轴,要么平行于Y轴的。这是和它的算法实现有关的。
这样会有什么限制呢,如果我们有一份这样的数据
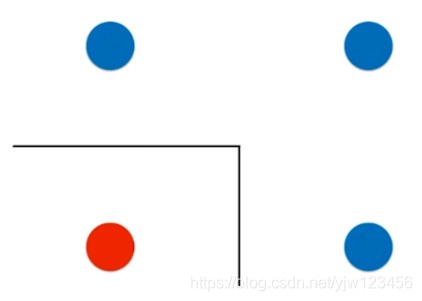
得到的决策边界就是这样的。这样的决策边界有可能无法反映真实数据的情况。
对于这份数据,有可能真正合理的决策边界是下面这样一根斜线:
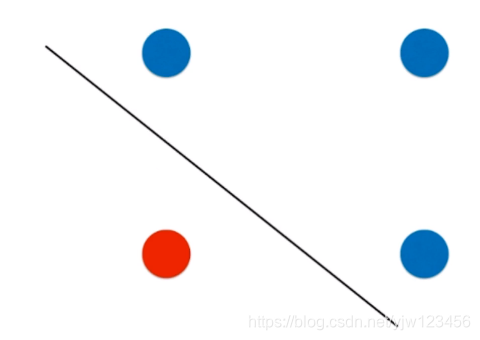
而决策树是永远无法产生这样一根斜线的。
还有一种情况是,我们的数据分布是这样的,此时用决策树也可以很容易的用一根垂直直线来划分,这没问题。
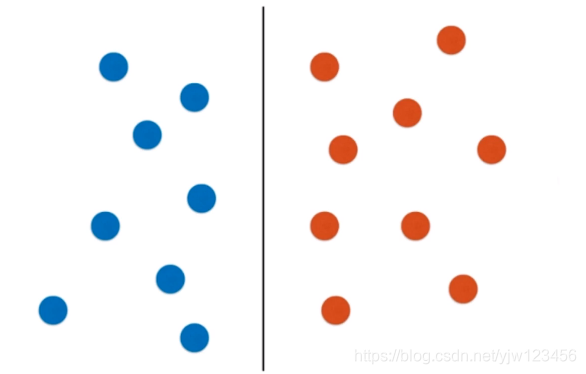
但是如果我们的数据有一定的倾斜,那么得到的分布图就是下面这样:

此时再用决策树的话,得到的决策边界很有可能就是下面这样的:
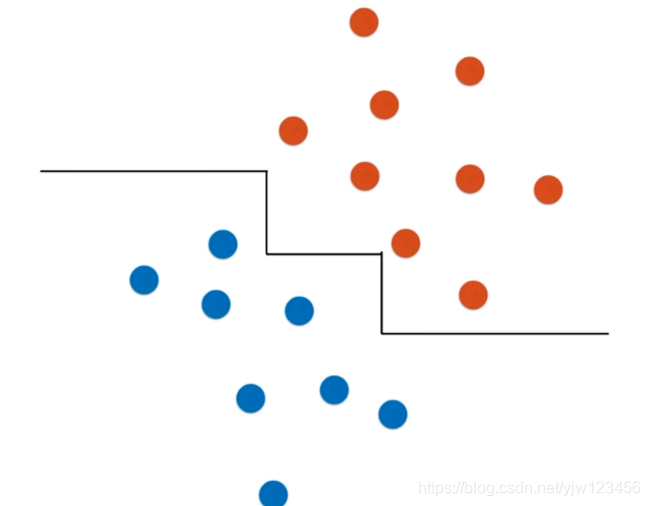
这样很可能是不对的,因为其实我们可以直接用一根斜线就能很好的划分了。
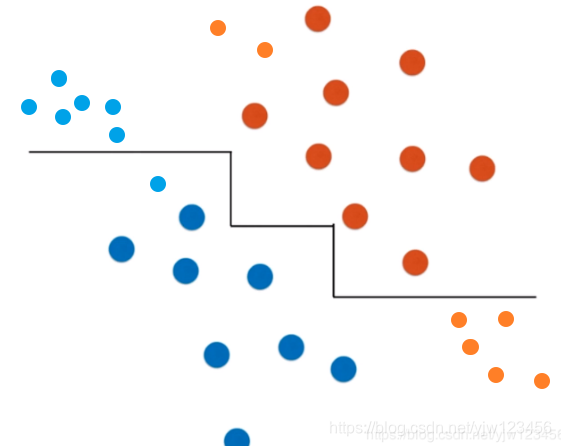
因为根据倾斜后的分布,可能有很多我们没有看到的数据其实是这样的,上面新的蓝色样本点和下面新的橙色样本点就被分类错误了。
决策树还有另外一个局限性是对个别数据敏感。
我们通过实例来说明这点:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data[:,2:] #只用后两个维度,方便可视化
y = iris.target
dt_clf = DecisionTreeClassifier(max_depth=2,criterion='entropy')
dt_clf.fit(X,y) #模型训练
plot_decision_boundary(dt_clf,axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.show()
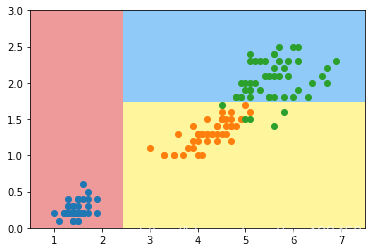
这个我们在上面介绍过,此时假如删掉一个特殊的样本点(个别数据),看下决策边界是怎样的:
X_new = np.delete(X,138,axis=0) #删掉索引为138的那一个数据
y_new = np.delete(y,138)
dt_clf2 = DecisionTreeClassifier(max_depth=2,criterion='entropy')
dt_clf2.fit(X_new,y_new) #模型训练
plot_decision_boundary(dt_clf2,axis=[0.5,7.5,0,3])
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.scatter(X[y==2,0],X[y==2,1])
plt.scatter(X[138,0],X[138,1]) #我们删掉的样本点
plt.show()
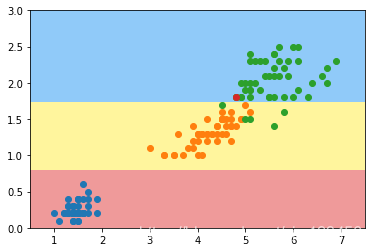
可以看到决策边界发生了很大的变化。上图中红色样本点就是我们刚才删掉的。
我们只是在训练时没有考虑这个样本点,得到的决策边界完全不同,这个说明了决策树对个别样本点是及其敏感的。其实这也是所有非参数学习的缺点。
决策树本身还是一个非常有用的机器学习算法,它主要用处体现在使用集成学习的方式创建随机森林。这个请听下篇文章分解。
