机器学习分享——逻辑回归推导以及 numpy 的实现

逻辑回归基本概念

什么是逻辑回归？
逻辑回归就是这样的一个过程：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

Logistic 回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别）

回归模型中，y是一个定性变量，比如y=0或1，logistic方法主要应用于研究某些事件发生的概率

概念解释

Logistic Regression推导过程

它的表达式是:

$f(x) = \frac{1}{1 + e^{-\theta}}$

$\theta = WX + B$

可以发现，经过sigmoid函数转换后, 输出值是在[0, 1]之间，可以认为输出是概率，下面就来详细的推导：

推导

为了计算方便, 我们只讨论二分类.

首先, 逻辑回归进行了一个假设，两个类别都服从均值不同，方差相同(方便推导)的高斯分布

$p(y|x=0) = \mu(\mu_0, \sigma)$

$p(y|x=1) = \mu(\mu_1, \sigma)$

高斯分布是比较容易处理的分布，根据中心极限定理也知道，最终会收敛于高斯分布。
从信息论的角度上看，当均值和方差已知时（尽管你并不知道确切的均值和方差，但是根据概率论，当样本量足够大时，样本均值和方差以概率1趋向于均值和方差），高斯分布是熵最大的分布，为什么要熵最大？因为最大熵的分布可以平摊你的风险（同一个值会有两个点可以取到, 不确定性很大），这就好比不要把鸡蛋放到同一个篮子里，想想二分查找中，为什么每次都是选取中间点作为查找点？就是为了平摊风险（假设方差相等只是为了计算方便）。

风险

$Risk(y=0|x) = \lambda_{00}P(y=0|x) + \lambda_{01}P(y = 1|x)$

$Risk(y=1|x) = \lambda_{10}P(y=0|x) + \lambda_{11}P(y = 1|x)$

其中， $Risk(y=0|x)$是把样本预测为0时的风险， $Risk(y=1|x)$是把样本预测为1时的风险，
$λ_{ij}$是样本实际标签为j时，却把它预测为i是所带来的风险。

我们认为预测正确并不会带来风险，因此 $λ_{00}$和 $λ_{11}$都为0，此外，我们认为当标签为0而预测为1 和 当标签为1而预测为0，这两者所带来的风险是相等的，因此 $λ_{10}$和 $λ_{01}$相等，方便起见，我们记为λ。但在一些领域里，比如医学、风控等，这些λ在大多数情况下是不相等的，有时候我们会选择“宁可错杀一一千也不能放过一个”;

那么我们简化后的表达式:

$Risk(y=0|x) = \lambda P(y = 1|x)$

$Risk(y=1|x) = \lambda P(y=0|x)$

根据最小化风险的原则，我们通常会选择风险较小的。

比如:

$Risk(y=0|x) < Risk(y=1|x)$

这就说明了预测为第0类的风险小于预测为第1类的风险。

可以得到：

$\frac{Risk(y=0|x)}{Risk(y=1|x)} < 1$

$\frac{P(y = 1|x)}{P(y=0|x)} < 1$

就是说明预测第1类的概率小于第0类的概率。

我们对不等式两边分别取对数

$log\frac{{P(y = 1|x)}}{{P(y=0|x)}} < 0$

根据贝叶斯公式：

$log\frac{P(x|y = 1)p(y=1)}{P(x|y=0)p(y=0)} < 0$

$log\frac{P(x|y = 1)}{P(x|y=0)} + log\frac{p(y=1)}{p(y=0)} < 0$

我们开始假设过，两个类别分别服从均值不等，方差相等的高斯分布，根据高斯分布的公式有：

高斯分布

$g(x) = \frac{1}{2\pi\sigma}e^{-\frac{(x - \mu)^2}{2\sigma^2}}$

忽略常数项（方差也是相等的）

$log\frac{P(x|y = 1)}{P(x|y=0)} + loge^{(\frac{(x - \mu_0)^2}{2\sigma^2} - \frac{(x - \mu_1)^2}{2\sigma^2})}$

$log\frac{P(x|y = 1)}{P(x|y=0)} + (\frac{(x - \mu_0)^2}{2\sigma^2} - \frac{(x - \mu_1)^2}{2\sigma^2}) < 0$

$log\frac{P(x|y = 1)}{P(x|y=0)} < \frac{(x - \mu_1)^2}{2\sigma^2} - \frac{(x - \mu_0)^2}{2\sigma^2}$

$log\frac{P(x|y = 1)}{P(x|y=0)} < \frac{\mu_0}{\sigma^2}x - \frac{\mu_1}{\sigma^2}x + C$

C是常熟，可以使用矩阵的表示。

$log\frac{P(x|y = 1)}{P(x|y=0)} < \theta{X}$

详细推导

对值取幂，以及等式取等号计算。

$\frac{P(y=1|x)}{P(y=0|x)} = e^{\theta x}$

$= \frac{P(y=1|x)}{1 - P(y=1|x)} = e^{\theta x}$

$= \frac{1 - P(y=1|x)}{P(y=1|x)} = e^{-\theta x}$

$= \frac{1}{P(y=1|x)} - 1 = e^{-\theta x}$

$= \frac{1}{P(y=1|x)} = e^{-\theta x} + 1$

$= P(y=1|x) = \frac{1}{e^{-\theta x} + 1}$

以下是实现的一些截图

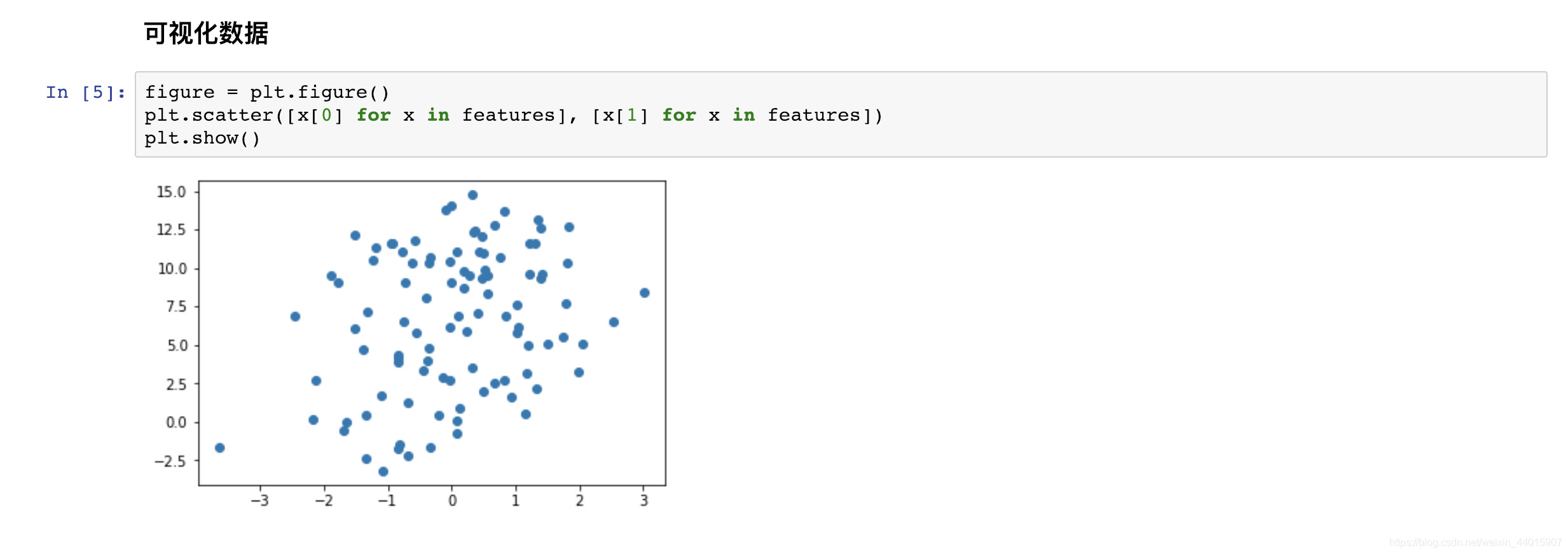
优化我们采用梯度下降算法

交叉熵损失函数

最终效果

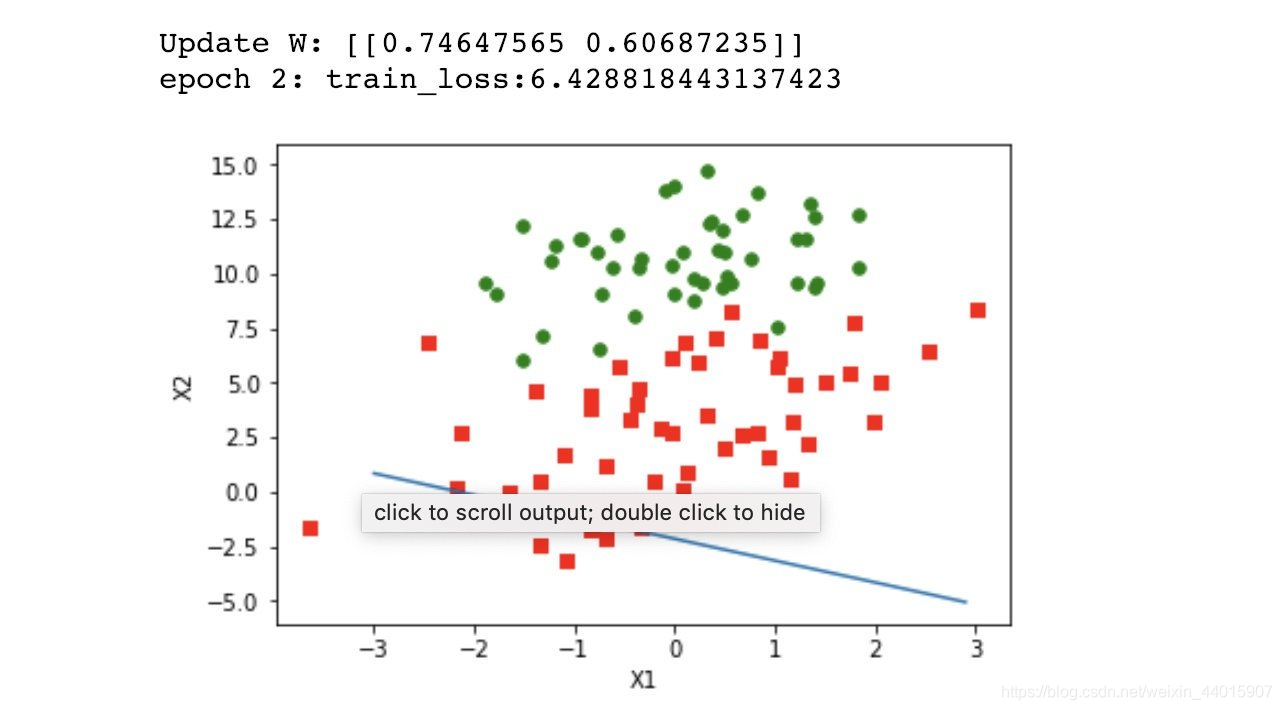
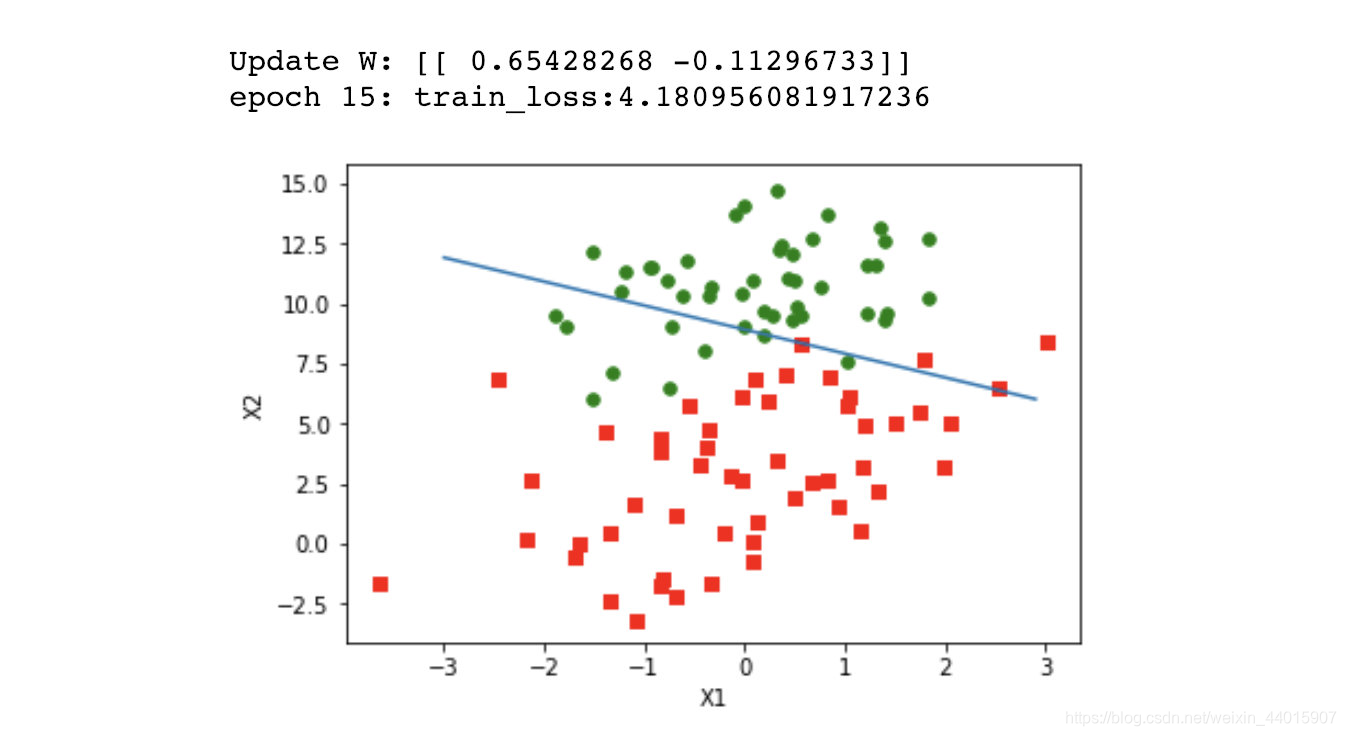
电脑端查看完整代码

——————————————————————————————————
Mo （网址：momodel.cn ）是一个支持 Python 的人工智能建模平台，能帮助你快速开发训练并部署 AI 应用。期待你的加入。