机器学习逻辑回归Python代码实现

分类问题不用线性回归的原因：

对于分类问题，y 取值为0 或者1。
如果使用线性回归，那么线性回归模型的输出值可能远大于1，或者远小于0。
导致代价函数很大。

逻辑回归模型（S 形函数）：

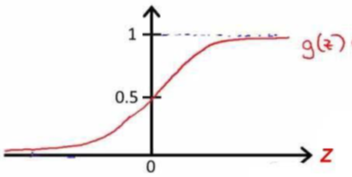
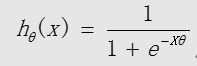
逻辑回归模型（S 形函数）

中间变量：

中间变量

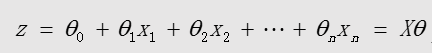
sigmoid函数的输出值永远在0 到1 之间：

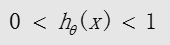
sigmoid函数的输出值永远在0 到1 之间:
在这里插入图片描述
逻辑回归模型的概率解释:
对于给定的输入变量x，根据选择的参数θ,计算输出变量y=1 的可能性（estimated probability）即:

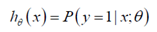
例如：如果对于给定的x，通过已经确定的参数计算得出hθ(x)=0.7，则表示有70%的几率y 为正向类，相应地y 为负向类的几率为1-0.7=0.3

逻辑回归的代价函数（交叉熵）：

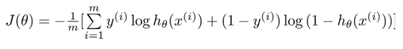
逻辑回归的代价函数（交叉熵）
该代价函数J(θ)是一个凸函数，有全局最优值；
因为代价函数是凸函数，无论在哪里初始化，最终达到这个凸函数的最小值点。

逻辑回归Python代码实现

（ex2data5.txt文件提取码:3d33）

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 能正确显示正负号

# 数据处理
# 加载数据
data = np.loadtxt('ex2data5.txt', delimiter=',')
# 切分
# 参数一，被切分的矩阵
# 参数二代表如何切分，[-1]代表-1之前的归为第一个返回值，其后归为第二个返回值
# 参数三，axis=0是横向切分，切分样本；axis=1是纵向切分，切分的是特征
x, y = np.split(data, [-1], axis=1)

# 特征缩放
mean = np.mean(x, 0)  # 平均数
sigma = np.std(x, 0, ddof=1)  # 标准差
x = (x-mean)/sigma  # 标准化特征缩放

# 拼接
m = len(x)
x = np.c_[np.ones((m, 1)), x]
y = np.c_[y]

# 切分训练集和测试集
num = int(m*0.7)
trainx, testx=np.split(x, [num])
trainy, testy=np.split(y, [num])

# sigmoid函数
def sigmoid(z):
    return 1.0/(1+np.exp(-z))

# 模型
def model(x, theta):
    z = x.dot(theta)
    h = sigmoid(z)   # 用sigmoid函数将连续值映射为0-1之间的概率值
    return h

# 交叉熵代价
def cost_function(h, y):
    m = len(h)
    J = -1.0/m*np.sum(y*np.log(h)+(1-y)*np.log(1-h)) 
    return J

# 梯度下降函数
def gradsDesc(x, y, alpha=0.001, count_iter=15000, lamda=0.5):
    m, n = x.shape
    theta = np.zeros((n, 1))
    jarr = np.zeros(count_iter)

    for i in range(count_iter):
        h = model(x, theta)
        e = h - y
        jarr[i] = cost_function(h, y)
        deltatheta = 1.0/m*x.T.dot(e)
        theta -= alpha*deltatheta

    return jarr, theta

# 模型精度，准确率
def accuracy(y, h):
    m = len(y)
    count = 0  #  统计预测值与真实值一致的样本个数
    for i in range(m):
        h[i] = np.where(h[i]>=0.5,1,0)  # 将预测值从概率值转换为0或1
        if h[i] == y[i]:
            count += 1

    return count/m

# 画图
def draw(x, y, theta):
    zeros = y[:,0]==0   # 选取y=0的行，其值为true
    ones = y[:,0]==1  # 选取y=1的行，其值为true

    # 画散点图
    plt.scatter(x[zeros,1],x[zeros,2],c='b',label='负向类')   # 画负向类的散点图
    plt.scatter(x[ones,1],x[ones,2], c='r', label='正向类')   # 画正向类的散点图

    # 画分界线
    # 取x1的最小值和最大值
    minx1 = x[:,1].min()
    maxx1 = x[:,1].max()

    # 计算x1的最大值和最小值在z=0上的对应的x2值
    minx1_x2 = -((theta[0]+theta[1]*minx1)/theta[2])
    maxx1_x2 = -((theta[0]+theta[1]*maxx1)/theta[2])

    # 以两个点坐标，画出z=0的决策边界
    plt.plot([minx1,maxx1], [minx1_x2, maxx1_x2])
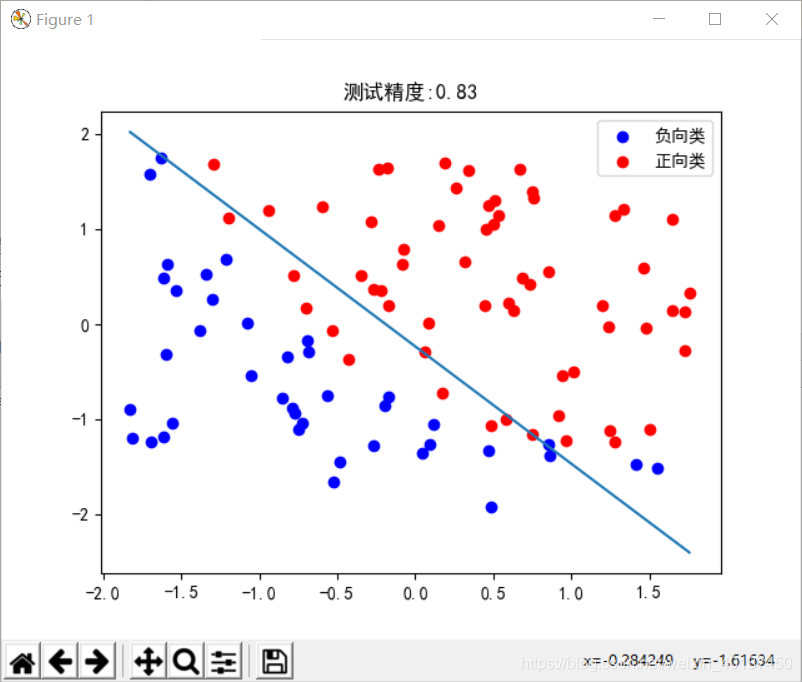
    plt.title('测试精度:%0.2f' % (accuracy(testy, testh)))
    plt.legend()
    plt.show()

# 训练模型
jarr, theta = gradsDesc(trainx, trainy)

# 计算测试值预测值
testh = model(testx, theta)

# 计算测试集预测精度
print('测试集预测精度：', accuracy(testy, testh))
# print('测试集预测值：', testh)

#画图
draw(x, y,theta)

# 画sigmoid函数
# a = np.arange(-10, 10)
# print(a)
# b = sigmoid(a)
# plt.plot(a,b)
# plt.show()

逻辑回归