NG机器学习总结-（四）逻辑回归以及python实现

在第一篇博客NG机器学习总结一中，我们提到了监督学习通常一般可以分为两类：回归和分类。线性回归属于回归问题，例如房价的预测问题。而判断一封邮件是否是垃圾邮件、肿瘤的判断（良性还是恶性）、在线交易是否欺诈都是分类问题，当然这些都是二分类的问题。

Email：Spam / Not Spam? （是否垃圾邮件）

Online Transactions : Fraudulent(Yes or No)？（是否欺诈）

Tumor : Malignant / Benign ? （肿瘤良性或恶性）

y = {0 , 1} 1： “positive class”（e.g. malignant） 0 ： “negative class” （e.g. benign）

这个时候如果我们进行分类，有一种办法是直接使用线性回归模型，然后将其结果隐射成0和1，例如结果大于0.5视为1，结果小于0.5的视为0，如下图肿瘤判断的例子。当然这种方法并不适用，因为分类并非线性回归模型。分类问题其实和回归问题有点相似，当然这里我们预测的值是离散的。

现在我们以二分类为例（当然这里大多数情况下是多类别的），例如垃圾邮件系统， $x^{(i)}$ 代表一封邮件的特征输入，1代表其是垃圾邮件，0代表其不是垃圾邮件，因此 $y\in (0,1)$ ，对于给定的 $x^{(i)}$ 其对应的输出 $y^{(i)}$ 也称为标签。

一、模型表示

这里我们尝试忽略y是离散值并使用以前的线性回归算法来处理分类问题，我们知道当 $y\in (0,1)$ ，线性回归算法的模型 $h_{\theta}(x)$ 取值大于1或者小于0这样来分类明显是不合适的，因此我们需要将我们的模型 $h_{\theta}(x)$ 的取值满足 $0\leqslant h_{\theta}(x)\leqslant 1$ ，这里我们使用sigmoid函数来包装我们的模型，如下，这就是逻辑回归模型。

$h_{\theta}(x)=g(\theta^{T}x)$

$z=\theta^{T}x$

$g(z)=\frac{1}{1+e^{-z}}$

Sigmoid函数是个很漂亮的S形，其作用可以将取值的范围友好的表示成[0,1]，而且受异常数据的影响较小，所以我们用sigmoid函数来包装就能很好的解决模型取值范围的问题，如下图所示：

（ps：其实，逻辑回归的本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用一个函数g(z)进行计算。g(z)函数可以将连续值映射到0和1上。也就是说线性回归的输出时y=f(x)=wx，而逻辑回归的输出是y=g(f(x))=g(wx)。）

这里写图片描述

二、决策边界

为了得到预测值是0或1的离散值，我们还需要将我们的模型输出约束一下：

$h_{\theta}(x)\geq 0.5\rightarrow y=1$

$h_{\theta}(x)< 0.5\rightarrow y=0$

观测sigmoid函数，我们可以发现：

当 $\theta^{T}x\geq 0\Rightarrow y=1$

当 $\theta^{T}x< 0\Rightarrow y=0$

因此这里的决策边界，就是可以将y=0和y=1的区域分开的一个条件。我们可以看下面的图，左边的坐标图是我们的数据分布位置，坐标图中左下角的圆圈是y=0的类别，右上角的红叉是y=1的类别，坐标图中的那条蓝色线就是我们要找的决策边界线。

这里我们的例子模型表示为：

$h_{\theta}(x)=g(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2})$

当我们取theta的值为（-3， 1， 1）的时候，可以看出 $-3+x_{1}+x_{2}= 0$ 是图中那条决策边界线。

上述中我们的模型的决策边界线是一条直线，当然有些时候 $h_{\theta}(x)$ 并不是一个线性模型，比如是多项式模型，如下图，我们的决策边界是一个圆形，有的时候也可能是不规则的形状。

这里我们的例子模型表示为：

$h_{\theta}(x)=g(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}x^{2}_{1} +\theta_{4}x^{2}_{2})$

当theta取值是（-1,0,0,1,1）的时候，可以看出 $-1+x^{2}_{1}+x^{2}_{2}=0$ 是我们的决策边界。

当我们的 $h_{\theta}(x)$ 模型更为复杂的时候，决策边界的形状可能就不是规则的。

三、损失函数

线性回归算法中其损失函数如下表示：

$J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2}$

当 $h_{\theta}(x)$ 是线性模型的时候这是一个凸函数，如果我们继续用这个来表示逻辑回归的损失函数的话，那么它就是一个非凸函数。在使用梯度下降法求解的时候不仅存在着局部最小值而且求导还异常困难。

这里NG直接给出逻辑回归的损失函数，如下两张图。(当时看视频的时候觉得他结合图解讲解为什么这样是可以表示逻辑回归的损失函数的，但是没有解释为什么用log函数来表示。其实这个可以通过逻辑回归模型本身推导得到，就是逻辑回归里面常用到的极大似然函数推导得到，有兴趣的可以上网搜索一下推导过程，这里不作过多的说明。)

$h_{\theta}(x)=g(\theta^{T}x)$

$Cost(h_{\theta}(x),y)=\begin{cases} -log(h_{\theta}(x)) & \text{ if } y=1 \\ -log(1-h_{\theta}(x))& \text{ if } y=0 \end{cases}$

当 $y=1$ 时，如果 $h_{\theta}(x)=1$ ，此时 $cost=0$ ；但是如果当 $h_{\theta}(x)\rightarrow 0$ ， $cost\rightarrow \infty$

反之

当 $y=0$ 时，如果 $h_{\theta}(x)\rightarrow 1$ ，此时 $cost\rightarrow \infty$ ；但是如果 $h_{\theta}(x)=0$ ， $cost=0$

简化这个损失函数如下：

$J(\theta)=\frac{1}{m} \sum_{i=1}^{m}Cost(h_{\theta}(x^{(i)}),y^{(i)}) \\=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]$

四、梯度下降法求解

逻辑回归的梯度下降法求解的过程其实是和线性回归的梯度下降法求解过程相似，不同的是损失函数的不同，接下来直接给出求解的结果：

$J(\theta)=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}logh_{\theta}(x^{(i)})+(1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]$

Want $min_{\theta}J(\theta)$

Repeat {

$\theta_{j}:=\theta_{j}-\alpha \frac{\partial }{\partial \theta_{j}}J(\theta)$

}

======================>下面的推导过程希望能够手动推导一遍，观察公式就可发现其和线性回归没什么两样，用代码实现的时候不过是h函数用sigmoid函数置换了一下。

Repeat {

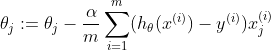
$\theta_{j}:=\theta_{j}-\frac{\alpha}{m} \sum^{m}_{i=1}(h_{\theta}(x^{(i)})-y^{(i)})x_{j}^{(i)}$

}

$h_{\theta}(x)=\frac{1}{1+e^{-\theta^{T}x}}$

五、多分类

上述中，我们使用的是二分类（y=0,y=1）来介绍逻辑回归的，但现实场景下大多是多类别的情况，比如邮件标签系统，邮件来自于工作、朋友、家人还是爱好？医学诊断中，感冒、流感还是没有生病？天气预测中，晴天、阴天、雨天还是雪天？

对于以上的多类别情况，如何利用逻辑回归算法来做呢？如果我们对每一个类别 $i$ 都训练一个逻辑回归模型并预测其值 $y=i$ 类别的概率值，那么当一个新的输入x，我们用每一个类别的逻辑回归模型预测其对应类别的输出值，然后取概率值最大的那个类别。如下图所示，对每一个类别建立逻辑回归模型的时候，其他的类别统一当成另一种类别（间接的转换成二分类的问题），这样就可以用逻辑回归来解决多类别的问题。

Train a logistic regression classifier $h_{\theta}^{(i)}(x)$ for each class $i$ to predict the probability that $y=i$

On a new input $x$ to make a prediction,pick the class $i$ that maximizes

$maxh^{(i)}_{\theta}(x)$

六、python实现

这里用python简单实现了逻辑回归算法（只使用了两个特征变量），然后利用逻辑回归从疝气病症预测病马的死亡率。

参见：Python实现线性回归和逻辑回归算法

NG机器学习总结-（四）逻辑回归以及python实现

猜你喜欢