机器学习|五个重要的抽样分布定理|15mins入门|概统学习笔记（二十一）

重要的抽样分布定理

• 前提：都是单个总体的样本，样本的数学期望和方差都易求，以此来求总体的数学期望和方差

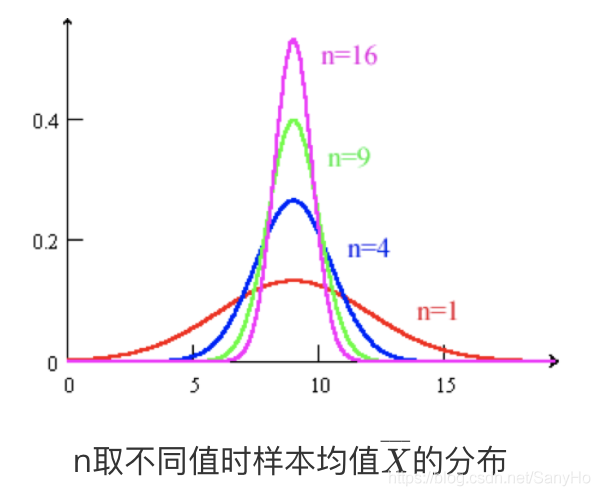
定理1（样本均值的分布）

• 定义：设 $X_1,X_2,...,X_n$是取自正态总体 $N(\mu,\sigma^2)$的样本，则有 $\overline X$~ $N(\mu,\frac{\sigma^2}{n})$

  因此 $\frac{\overline X - \mu}{\sigma/\sqrt{n}}$~ $N(0,1)$

• 作用：可推测总体的 $\mu、\sigma^2$值，但前提是至少有一个已知

  证明：

$E(\overline X)=E(\frac{1}{n}\sum_{i=1}^nX_i)=\frac{1}{n}E(\sum_{i=1}^nX_i)=\frac{1}{n}(\sum_{i=1}^nEX_i)=\frac{1}{n}\times n \times\mu=\mu$

$D(\overline X)=D(\frac{1}{n}\sum_{i=1}^nX_i)=\frac{1}{n^2}D(\sum_{i=1}^nX_i)=\frac{1}{n^2}(\sum_{i=1}^nDX_i)=\frac{1}{n^2}\times n\times \sigma^2 = \frac{\sigma^2}{n}$

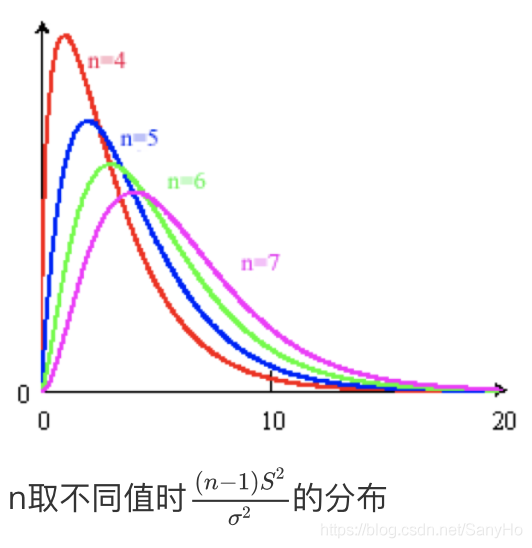
定理2 （样本方差的分布）

• 定义：设 $X_1,X_2,...,X_n$是取自正态总体 $N(\mu,\sigma^2)$的样本， $\overline X$和 $S^2$分别为样本均值和样本方差，则有 $\frac{(n-1)S^2}{\sigma^2}$~ $\chi^2(n-1)$，且 $\overline X$和 $S^2$相互独立。

• 作用：在总体的 $\mu$未知时，可推测总体的 $\sigma^2$的值。

定理3（样本的均值与方差的联合分布）

• 设 $X_1,X_2,...,X_n$是取自正态总体 $N(\mu,\sigma^2)$的样本， $\overline X$和 $S^2$分别为样本均值和样本方差，则有

  $\frac{\overline X-\mu}{S/\sqrt{n}}$~ $t(n-1)$

• 作用：在总体的 $\sigma^2$未知时，可推测总体的 $\mu$值

• 证明：

  由定理一可知： $\frac{\overline X-\mu}{\sigma/\sqrt{n}}$~ $N(0,1)$

  由定理二可知： $\frac{(n-1)S^2}{\sigma^2}$~ $\chi^2(n-1)$

  且两者相互独立，由t分布的定义可知

  $\frac{\frac{\overline X-\mu}{\sigma/\sqrt n}}{\sqrt{\frac{(n-1)S^2}{\sigma^2(n-1)}}}$~ $t(n-1) \quad \to \quad \frac{\overline X-\mu}{S/\sqrt{n}}$~ $t(n-1)$

定理4 （两总体样本均值差的分布）

• 设 $X$_{$N(\mu,\sigma^2)$，$Y$} $N(\mu_2,\sigma^2)$,且X与Y独立， $X_1,X_2,...,X_{n_2}$是取自X的样本， $Y_1,Y_2,...,Y_{n_2}$取自Y的样本， $\overline X$和 $\overline Y$分别是这两个样本的样本均值， $S_1^2$和 $S_2^2$分别是这两个样本的样本方差，则有

  $\frac{\overline X-\overline Y-(\mu_1-\mu_2)}{\sqrt{\frac{(n-1)S_1^2+(n_2-1S_2^2)}{n_1+n_2-2}}\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$~ $t(n_1+n_2-2)$

定理5 （两总体样本方差比的分布）

• 设 $X$_{$N(\mu,\sigma^2)$，$Y$} $N(\mu_2,\sigma^2)$,且X与Y独立， $X_1,X_2,...,X_{n_2}$是取自X的样本， $Y_1,Y_2,...,Y_{n_2}$取自Y的样本， $\overline X$和 $\overline Y$分别是这两个样本的样本均值， $S_1^2$和 $S_2^2$分别是这两个样本的样本方差，则有

  $\frac{S_1^2/\sigma_1^2}{S_2^2/\sigma_2^2}$~ $F(n_1-1,n_2-1)$

• 作用：可推测两个总体的方差比值