统计三大分布
1.
χ2分布
-
本质:
χ2分布是由正态分布派生出来的一种分布
-
定义:设
X1,X2,...,Xn相互独立,都服从正态分布
N(0,1),则称随机变量:
χ2=X12+X22+⋅⋅⋅+Xn2
所服从的分布为自由度为n的
χ2分布。记为:
χ2~
χ2(n)
χ2分布的密度函数为:
f(x;n)={2n/2Γ(2n)1x2n−1exp(−2x)0x>0其他
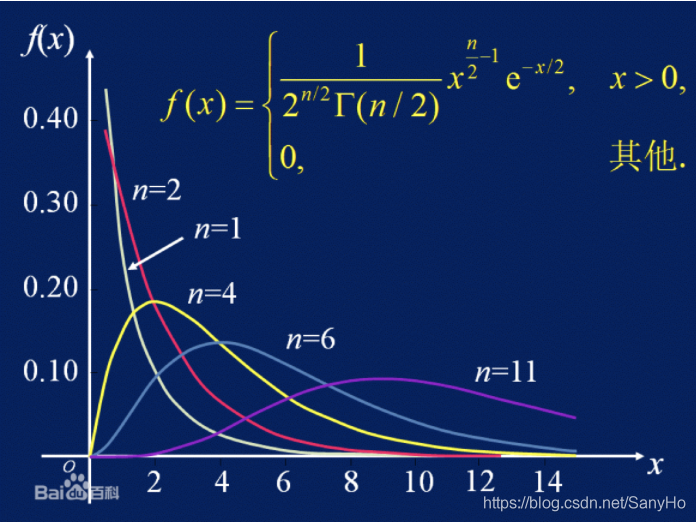
其中,伽马函数
Γ(x)通过积分
Γ(x)=∫0∞exp(−t)tx−1dtx>0
Γ函数的性质:
Γ(a+1)=aΓ(a)Γ(1)=Γ(0)=1Γ(n+1)=n!Γ(21)=(
π)
-
χ2分布性质
-
设
X1,X2,...,Xn相互独立,都服从正态分布
N(μ,σ2),则
χ2=σ21∑i=1n(Xi−μ)2~
χ2(n)
-
设
X1$\chi^2(n_1)$,$X_2$
χ2(n2),且
X1,
X2相互独立,则
X1+X2~
χ2(n1+n2)
这个性质叫
χ2分布的可加性
-
若
X~
χ2(n),则
E(X)=n,D(X)=2n
推论:应用中心极限定理得,若
X~
χ2(n),则当n充分大时,
2n
X−n的分布近似正态分布
N(0,1)
-
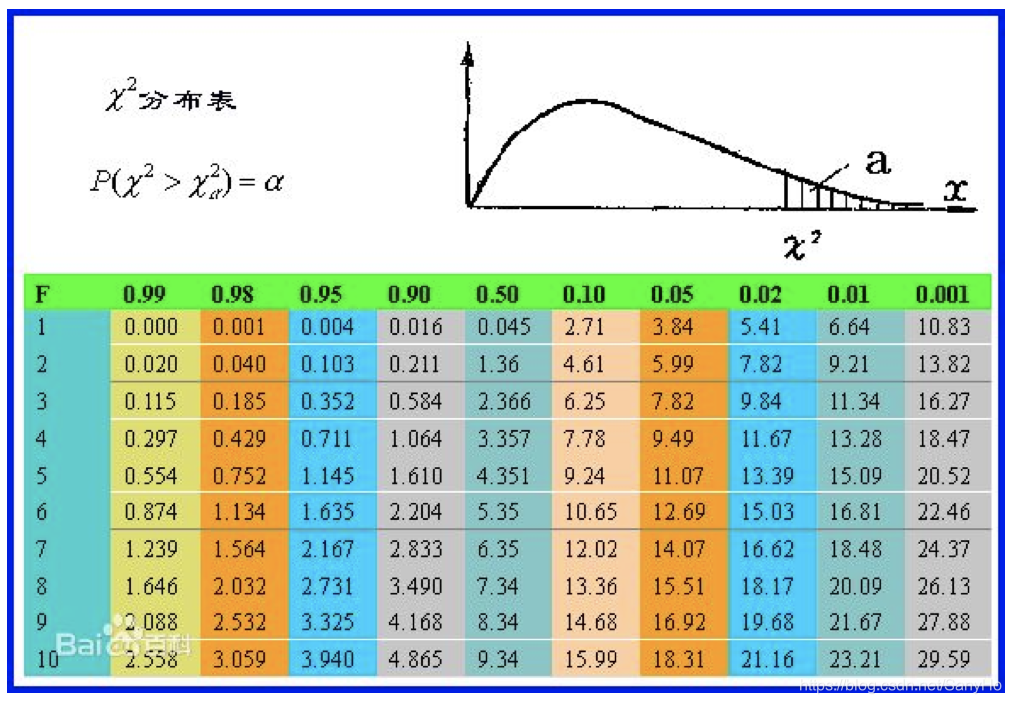
χ2分布的分位点:对于给定的正数
α(0<α<1),称满足条件
P{χ2>χα2(n)}=∫χα2(n)+∞f(y)dy=α
的点
χα2(n)为
χ2(n)分布上的
α分位点,
α是概率
2. t分布(学生氏分布)
-
定义:设
X$N(0,1)$,$Y$
χ2(n),且X与Y相互独立,则称变量
T=Y/n
X所服从的分布为自由度为n的t分布。记为
T~
t(n).
T的密度函数为:
f(x;n)=Γ(n/2)nπ
Γ(n+1)/2(1+nx2)−2n+1
具有自由度为n的t分布的随机变量T的数学期望和方差为:
E(T)=0;D(T)=n−2n,(n>2)
t分布的密度函数关于x=0对称,且
lim∣x∣→∞f(x;n)=0
当n充分大时,其图形类似于标准正态分布密度函数的图形。
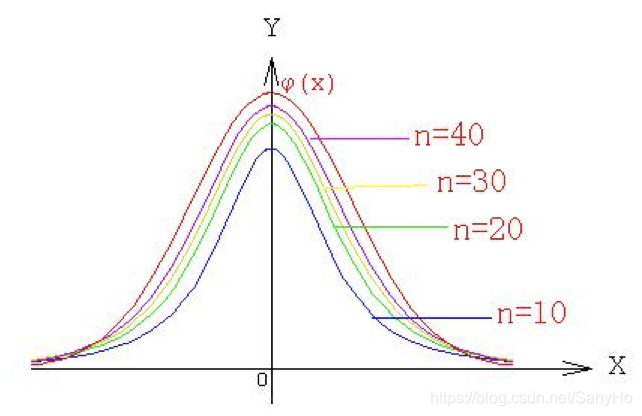
不难看出,当n充分大时,t分布近似
N(0,1)分布。但对于较小的n,t分布与
N(0,1)分布相差很大
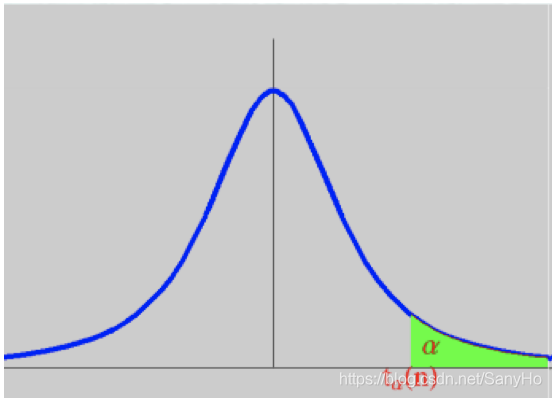
由t分布上
α分位点的定义及
h(t)图像的对称性可知
t1−α(n)=−tα(n)
3.F分布
-
定义:设
X$\chi^2(n_1)$,$Y$
χ2(n2),X与Y相互独立,则称统计量
F=Y/n2X/n1,服从自由度为
n1及
n2的F分布,
n1称为第一自由度,
n2称为第二自由度,记作
F~
F(n1,n2)
由定义可见,
F1=X/n1Y/n2~
F(n2,n1)
若X~
F(n1,n2),X的概率函数为
f(x;n1,n2)={Γ(2n1)Γ(2n2)Γ(2n1+n2)(n2n1)(n2n1x)2n1−1(1+n2n1x)−2n1+n20x≥0x<0
X的数学期望为
E(X)=n2−2n2若n2>2
即它的数学期望并不依赖于第一自由度
n1.

若随机变量X服从分布
F(n,n),则
P{X≤1}=P{X≥1}=0.5
-
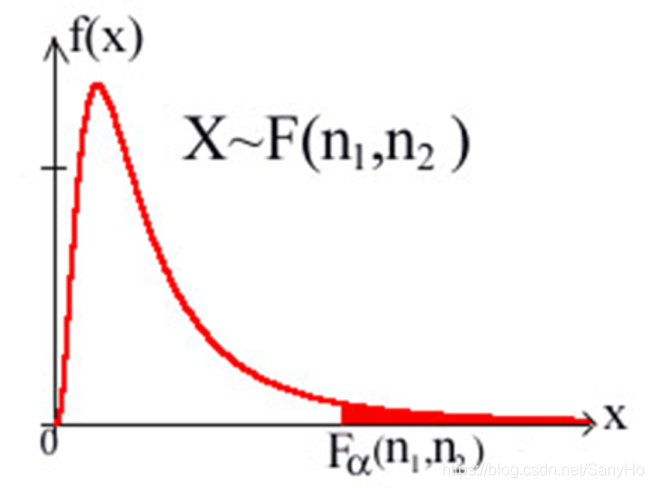
F分布的分位点
对于给定的
α(0<α<1),称满足条件
P{F>Fα(n1,n2)}=∫Fα(n1,n2)+∞h(t)dt=α
的点
Fα(n1,n2)为
F(n1,n2)分布的上
α分位点,
α是概率
关于F分布的上
α分位点的性质:
F1−α(n1,n2)=Fα(n2,n1)1






