机器学习|二项分布（贝努里概型、二项分布的泊松近似，正态近似）|10mins入门|概统学习笔记（五）

二项分布

1.贝努里概型

• 定义：n次独立重复试验称作n重贝努里试验，每次试验成功的概率都是p，失败的概率都是q=1-p

• 内容：

  用X表示n重贝努里试验中事件A（成功）出现的次数，则
  $P(X=k)=C_n^kp^k(1-p)^{n-k},k=0,1,...,n$
  不难验证:
  $a.P(X=k)\geq0 \\ b.\sum_{k=0}^nP(X=k)=1$

• 二项分布

  • 称 $r.v X$服从参数为n和p的二项分布，记作X~B(n,p)

  • 二项分布描述的是n重贝努里试验中出现“成功”次数X的概率分布

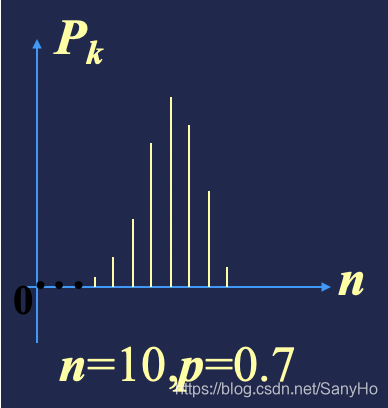
  • 图形特点：对于固定n及p，当k增加时，概率P（X=k）先是增加至达到最大值，随后单调减少。

    • 当(n+1)p不为整数时，二项概率 $P(X=k)$在 $k=[(n+1)p]$达到最大值。

      ([x]表示不超过x的最大整数)

    • 当(n+1)p为整数时，二项概率 $P(X=k)$在 $k=(n+1)p$和 $k=(n+1)p-1$达到最大值。

  • 当n=1时， $P(X=k)=p^k(1-p),k=0,1$。称X服从0-1分布

• 使用条件：

  • 每次试验条件相同

  • 每次试验只考虑两个互逆结果 $A$或 $\overline A$，且 $P(A)=p,P(\overline A)=1-p$

  • 各次试验相互独立

2. 二项分布的泊松近似

• 背景：当试验次数n很大时，计算二项概率变得很麻烦。

  • 如1000件产品，只有一件次品，要求有放回地抽5000次，其中至少5次出现次品的概率。

    则要计算
    $P(X>5)=\sum^{5000}_{k=6}P(X=k)=\sum^{5000}_{k=6}C^k_{5000}(\frac{1}{1000})^k(\frac{999}{1000})^{5000-k}$
    因此必须寻求近似方法，由此引入二项分布的泊松近似

• 泊松定理

  设 $\lambda$是一个正整数， $p_n=\frac{\lambda}{n}$,则有
  $lim_{n\to \infty}C_n^kp_n^k(1-p_n)^{n-k}=e^{-\lambda}\frac{\lambda^k}{k!},\space k=0,1,2,...$
  定理的条件意味着当n很大时， $p_n$必定很小。因此，泊松定理表明，当n很大，p很小时有以下近似式：
  $C_n^kp_n^k(1-p_n)^{n-k}\approx e^{-\lambda}\frac{\lambda^k}{k!}, \space \lambda=np$
  实际计算中, $n\geq 100,np\leq 10$时近似效果就很好。

3. 二项分布的正态近似

• 定理（棣莫佛-拉普拉斯定理）

  设随机变量 $Y_n$服从参数 $n,p(0<p<1)$的二项分布，则对任意x，有
  $lim_{n\to \infty}P\{\frac{Y_n-np}{\sqrt{np(1-p)}}\leq x\}=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}exp(-\frac{t^2}{2})dt$
  当n很大， $0<p<1$是一个定值时，或者说， $np(1-p)$也不太小时，二项变量 $Y_n$的分布近似正态分布 $N(np,np(1-p))$.

  实用中， $n\geq30$, $np\geq 10$时，正态近似的效果较好