楔子
在上一篇里,介绍了离散型随机变量。但实际上,取值于连续区域的随机变量的应用领域也是十分普遍的。比如汽车行驶的速度、设备连续正常运行的时间等,这些在实际应用中都非常广泛,连续型随机变量能够刻画一些离散型随机变量无法描述的问题。
概率密度函数
我们说离散型随机变量对应的取值个数是可数的,它的分布列对应概率质量函数PMF;而连续性随机变量对应的取值数量则往往是不可数的,而离散型随机变量分布列则对应概率密度函数PDF,这两者的概念是完全相对应的。我们可以说该随机变量对应的分布列,也可以说该随机变量对应的概率函数(根据离散或连续,可以是质量或密度)
我们回顾一下离散型随机变量分布列:
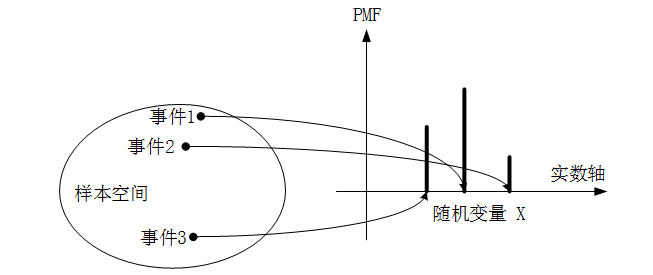
通过将三个事件所对应的概率值进行相加,就能得到这个事件集合所对应的总的概率:P(X∈S) = Px(1) + Px(2) + Px(3)
而连续型随机变量和离散型随机变量最明显的不同点是,连续型随机变量的个数是无限的、不可数的,不是像这样直接简单相加,而是在实轴的区间范围内,对概率密度函数进行积分运算。

这里,我们要对概率密度函数的特殊性进行强调:
第一:实数轴上单个点的概率密度函数 PDF,其值不是概率,而是概率律,因此他的取值是可以大于 1 的。第二:连续型随机变量的概率,我们一般讨论的是在一个区域内取值的概率,而不是某个单点的概率值。实际上,在连续区间内讨论单个点是没有意义的。
连续型随机变量在一个区间内取值的概率,我们可以通过求积分来计算解决。例如上图中,随机变量在区间[a, b]内的概率即为:
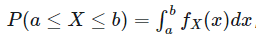
也就是图中阴影区间内的面积。因此这也进一步印证了上面的第二条结论,也就是说我们关注的不是单个点而是一个取值区间的概率计算。
当x=a时,P(a≤X≤a) = 0,因此即便区间两边相等也无所谓同理P(a≤ X ≤b) = P(a≤ X <b) = P(a< X ≤b) = P(a< X <b)
同样的,我们继续进行类比,连续型随机变量概率的非负性和归一性体现在:
非负性:对一切的x都有fX(x) > 0
归一化:P(-∞ ≤ X ≤ +∞) = 1
连续型随机变量的期望与方差
千万不要到了这个连续型的新场景下就慌了手脚。在离散型随机变量中,我们通过分布列,求得加权的均值,即获得了离散型随机变量的期望。即:每一个可能的取值乘上对应的概率再相加
那么在连续型随机变量的场景下,我们死抠定义,期望 E[X] 的核心定义是大量独立重复试验中,随机变量 X 取值的平均数(可不是直接将可能的取值加起来再除以总数,而是像我们上面说的那样,可能的取值乘上对应的概率、再分别相加,要考虑到权重在里面。),那么我们此时将分布列替换成概率密度函数 PDF,求和替换成求积分就可以了,即:

方差也是一样,扣定义:方差是随机变量到期望的距离的平方的期望:
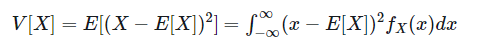
关于方差可能比较绕,我们先不考虑随机变量、而是考虑一组数字10 20 30 40,我们说这一组值的方差就等于
每一个值到平均值距离的平方然后再相加、除以总个数。现在换成离散型随机变量,那么把平均值换成期望,先计算每一个值到期望距离的平方,然后不要相加、除以总个数,而是各自乘上对应的概率然后直接相加即可,因为要考虑到权重。那么对于连续型就是把概率质量函数换成概率密度函数即可,所以说方差是随机变量到期望的距离的平方的期望
然后我们来看几个非常重要的连续型随机变量的实际举例
正态分布
正态分布是连续型随机变量概率分布中的一种,你几乎能在各行各业中看到他的身影,自然界中某地多年统计的年降雪量、人类社会中比如某地高三男生平均身高、教育领域中的某地区高考成绩、信号系统中的噪音信号等,大量自然、社会现象均按正态形式分布。
正态分布中有两个参数,一个是随机变量的均值 μ,另一个是随机变量的标准差 σ,他的概率密度函数 PDF 为:
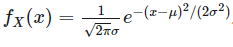
当我们指定不同的均值和标准差参数后,就能得到不同正态分布的概率密度曲线,正态分布的概率密度曲线形状都是类似的,他们都是关于均值 μ 对称的钟形曲线,概率密度曲线在离开均值区域后,呈现出快速的下降形态。另外,当均值 μ=0,标准差 σ=1 时,我们称之为标准正态分布。
import numpy as np
from scipy.stats import norm
import plotly.graph_objs as go
x = np.linspace(-10, 10, 1000)
normal_1 = norm(loc=0, scale=1).pdf(x)
normal_2 = norm(loc=1, scale=2).pdf(x)
normal_3 = norm(loc=-1, scale=2).pdf(x)
trace1 = go.Scatter(x=x,
y=normal_1,
line={"width": 4, "color": "green"},
name="均值为0、方差为1")
trace2 = go.Scatter(x=x,
y=normal_2,
line={"width": 4, "color": "yellow"},
name="均值为1、方差为2")
trace3 = go.Scatter(x=x,
y=normal_3,
line={"width": 4, "color": "red"},
name="均值为-1、方差为2")
fig = go.Figure(data=[trace1, trace2, trace3], layout={"template": "plotly_dark"})
fig.show()
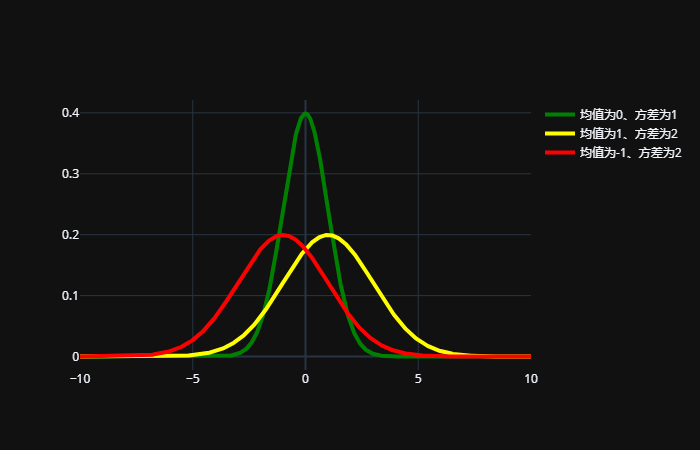
我们看到对于正太分布来讲,平均值就是曲线顶点的x轴坐标。平均值增大,那么曲线会向右移动、反之向左移动。方差越大则是曲线越瘦高,越小则曲线越矮胖。
指数分布
我们再来看看我们要讲的第二种连续型随机变量,指数随机变量。指数随机变量的用处非常广泛,他一般用来表征直到某件事情发生为止所用的时间。
比如,从现在你观察的时间开始算起,一台仪器设备的使用寿命终止还剩的时间、一个灯泡直到用坏了还剩的时间、陨石掉入地球沙漠还需要的时间等。
指数随机变量 X 的概率密度函数为:

其中,指数分布的参数是 λ,且必须满足 λ>0,指数分布的图形特征是当随机变量 X 超过某个值时,概率随着这个值的增加而呈指数递减。讨论指数分布的概率特性时,我们一般着重注意三个方面的内容:
-
第一个:随机变量 X 超过某个指定值 a 的概率,当然此处需要满足 a≥0。依照定义,我们有: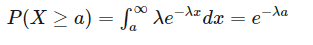
-
第二个:随机变量 X 位于区间 [a,b] 内的概率,实际上也很简单:
-
第三个:也就是整个指数分布的数字特征,同时也包含参数 λ 的物理含义。我们在这里可以通过期望和方差的定义,直接用积分求得,这里就不多赘述,直接拿出结论:E[X] = 1 / λ、V[X] = 1 / λ^2