ニューラルODE
ODE常微分方程式
オイラー法解法:オイラー法解法処理は再帰的処理であり、ニュートン法や勾配降下法と考え方が似ています。そして、関数を離散化し、小さなセグメントに分割して解決します。オイラー法で解かれる常微分方程式の形式は通常次のとおりです。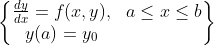
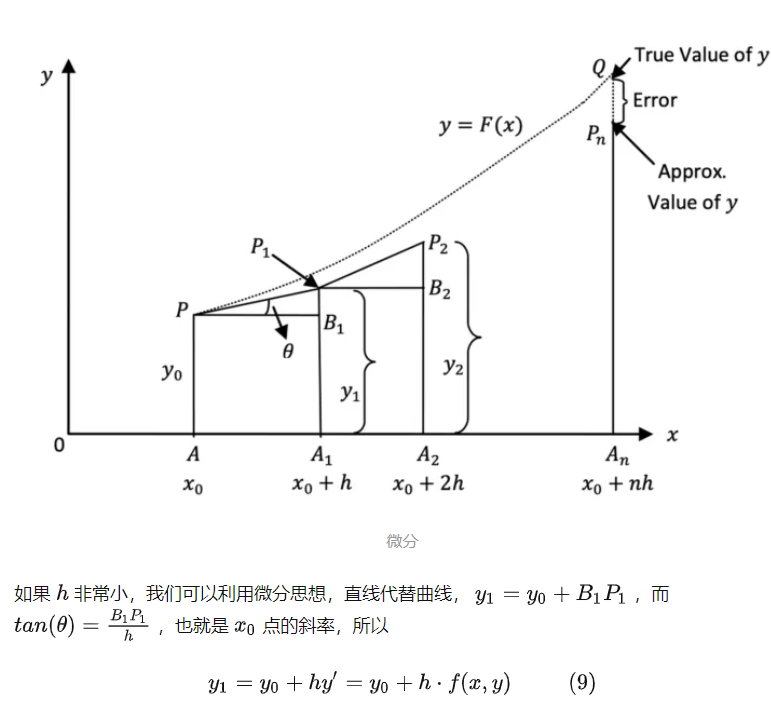
Zhihu Neural ODE の画像、結局世界は連続です
オイラー法を使用して方程式を解く例:常微分方程式 (ODE) コードの近似解を求めるオイラー法

からの抜粋:
import numpy as np
import matplotlib.pyplot as plt
y0=1 #初始条件
def f(x,y):
return y-2*x/y
def Eular(y0,n,f):
y=[y0] #储存各个点的函数值
y0=y0
for x in np.linspace(0,1,n):
'''求函数在区间[0,1]近似解,分n份'''
y1=y0+f(x,y0)/n
y.append(y1)
y0=y1
return y
y=Eular(1,10,f=f)
x=np.linspace(0,1,len(y))
plt.plot(x,y,color='blue')
plt.show()
Divine 常微分方程式:
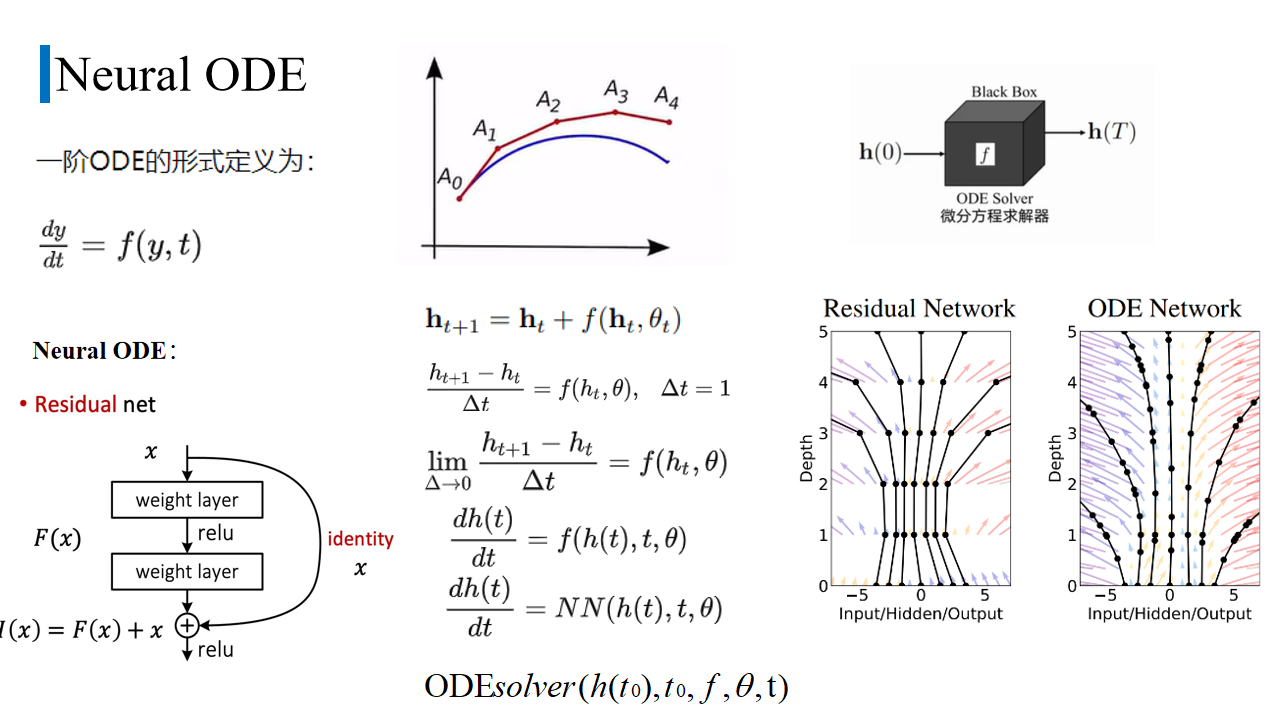
常微分方程式を解くときは、ODEsolver を使用できます。電卓に相当するもので、ニューラルネットワークの初期値h(t0)と所要時間tを与えると自動で計算してくれます。

ODEsolver は基本的に数値解法を使用して T を段階的に解決します。wi+1 を求める数値的方法は、wi にステップ h* 間隔の平均変化率を加えたものです。アルゴリズムが異なれば、平均変化率を決定する方法も異なります。
オイラー法の平均変化率は点 ti の導関数をとります。
改善されたオイラー法:
まずオイラー法を使用して、現在の点から wi+1' 離れた次の点の値を見つけてから、現在の点の勾配の平均を使用します。予測ポイントの勾配を区間平均変化率として計算し、実際の wi+1 ポイントの値を求めます。
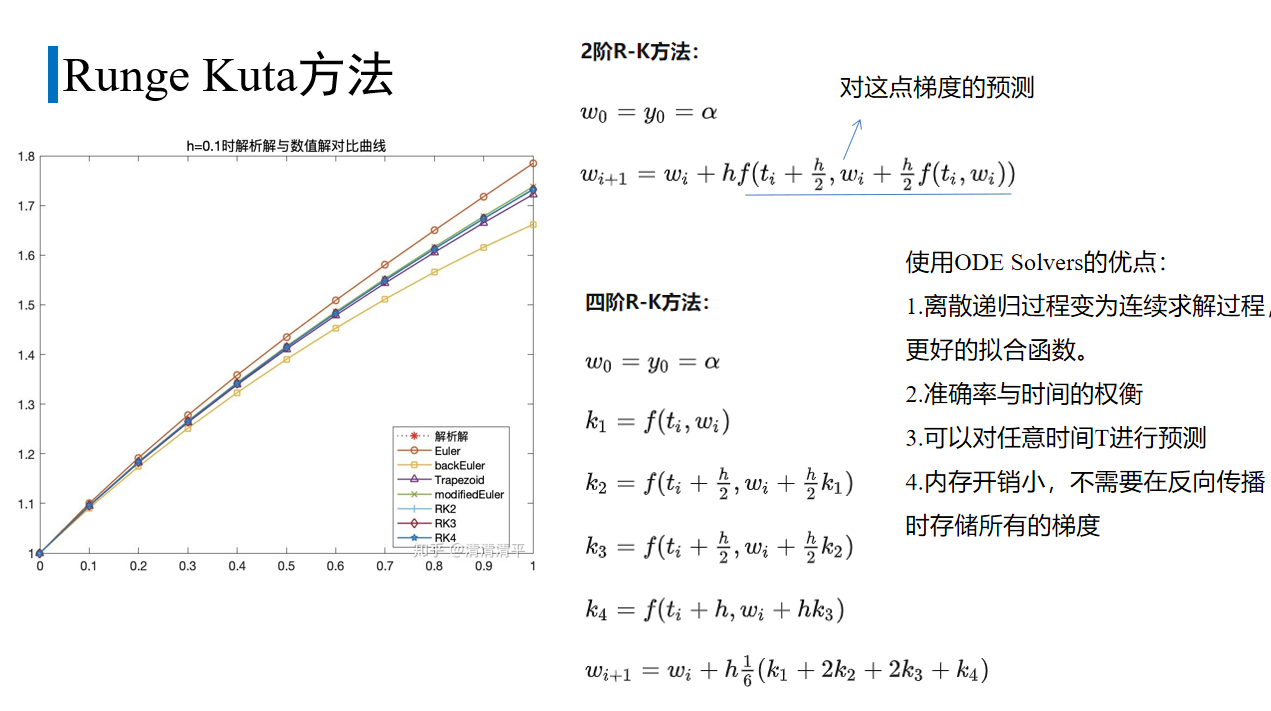
ルンゲ・クッタ法はオイラー法よりも精度が高くなります。
rk2:
まずオイラー法を使用して h/2 での勾配を推定し、次にこの値を使用して wi+1 を計算します。
rk4:
wi+1 は、wi とステップ サイズ h の 4 つの勾配の加重平均によって決定されます。
k 1 は、このステップの開始時にオイラー法を使用した導関数です。k
2 は、k 1 に基づく、h/2 での導関数です。k
3 は、引き続き k2 に基づく h/2 での導関数です。k
4 は、導関数です。 at h/2、k2 に基づく k3 に基づく終点 h での導関数。
いくつかの数値解を実際の解と比較すると、RK 法の精度は比較的高くなります。
一般的な逆伝播アルゴリズムでは、順方向計算プロセス中に活性化マップを保存する必要があります。ODE は、アクティベーション マップを保存せずに勾配を計算できるアジョイント法を使用します。
アジョイント法では逆過程を新しい ODE 初期値解問題 (IVP) とみなすため、勾配値は ODE ソルバーを使用して直接計算されます。これによりメモリ使用量が削減されます。
応用:
最近の研究では、勾配降下アルゴリズム (GDA) の反復プロセスは、常微分方程式 (ODE) のオイラー離散化と見なすことができることがわかりました。
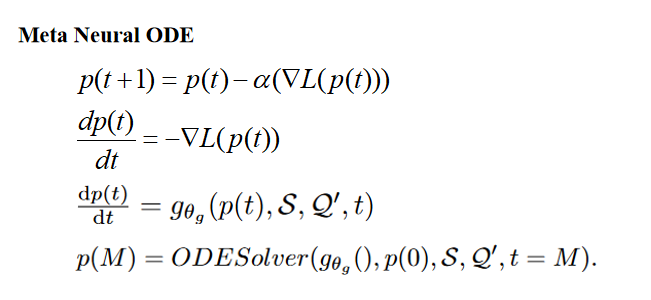
必要なパラメータの勾配を推定するネットワークを設計します。ここではプロトタイプ p です。
勾配を推定した後、odesolver を使用して、指定された瞬間における p の値を解きます。この指定されたモーメント M は、損失を収束させるためにトレーニング段階で使用されるハイパーパラメータによって決定されます。