高等数学 · 第四章 微分中值定理与导数的应用

第一节 微分中值定理

一、费马定理

定理4.1 （费马定理）

若函数 $f(x)$ 在 $x_0$ 处可导，并且在 $x_0$ 的某邻域内恒有 $f(x) \le f(x_0)$ 或 $f(x) \ge f(x_0)$ 则 $f'(x_0) = 0$.
证明：不妨设在 $x_0$ 的某邻域内恒有 $f(x) \le f(x_0)$，故 $\forall x_0 + \Delta x \in U(x_0), f(x_0 + \Delta x) \le f(x_0)$，则 $f'(x_0) = \lim \limits_{\Delta x \to 0} \cfrac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} =$ $\begin{cases} {f'_-(x_0) \ge 0 (\Delta x \to 0^-)} \\ {f'_+(x_0) \le 0 (\Delta x \to 0^+)} \end{cases}$ $\to f'(x_0) = 0$

费马定理的几何意义

如果 $f(x_0)$ 是函数 $f(x)$ 在 $x_0$ 的某领域内的最大值或最小值，并且曲线 $y = f(x)$ 在点 $(x_0, f(x_0))$ 处有切线，则切线一定是水平的。

补充：极值的定义

如果 $f(x_0)$ 在 $I$ 的某领域内恒有 $f(x) \le f(x_0)$ 或 $f(x) \ge f(x_0)$，则称 $f(x_0)$ 为 $f(x)$ 的一个极大值或极小值，而称 $x_0$ 为极大值点或者极小值点。极大值与极小值统称为 极值，极大值点和极小值点统称为极值点。
如果 $f'(x_0) = 0$， 则称 $x_0$ 为函数 $f(x)$ 的一个驻点。
因此，费马定理又可表述为：可导的极值点一定是驻点。

二、罗尔定理

定理4.2 罗尔(Rolle)定理

$y = f(x)$ 满足：

1. 在区间 $[a, b]$ 上连续
2. 在区间 $(a, b)$ 内可导
3. $f(a) = f(b)$

$\to$ 在 $(a, b)$ 内至少存在一点使 $f'(\xi) = 0$
证明：因为 $f(x)$ 在 $[a, b]$ 上连续，故在 $[a, b]$ 上取得最大值 $M$ 和最小值 $m$.
若 $M = m$，则 $f(x) = M, x \in [a, b]$, 因此 $\forall \xi \in (a, b)，f'(\xi) = 0$.
若 $M \gt m$, 则 $M$ 和 $m$ 中至少有一个与端点值不等，不妨设 $M \neq f(a)$，则至少存在一个 $\xi \in (a, b)$， 使 $f(\xi) = M$, 则由费马定理得 $f'(\xi) = 0$.

证明题

已知 $f(x) = x \sqrt{3 - x}$，求证： 方程 $f'(x) = 0$ 在 $(0,3)$ 内至少一根。
解： $\because f(x)$ 在 $[0, 3]$ 上连续， 在 $(0, 3)$ 内可导，且 $f(0) = f(3) = 0$。
$\therefore f(x)$ 在 $[0, 3]$ 上满足罗尔定理的条件，故至少有一个点 $\xi \in (0,3)$，使得 $f'(\xi) = 0$，也就是方程 $f'(x) = 0$ 在 $(0, 3)$ 内至少有一根。

三、拉格朗日中值定理

定理4.3 拉格朗日中值定理

设函数 $y = f(x)$ 满足：

1. 在区间 $[a, b]$ 上连续
2. 在区间 $(a, b)$ 上可导

$\to$ 至少存在一点 $\xi \in (a, b)$，使 $f'(\xi) = \cfrac{f(b) - f(a)}{b - a}$

证明：问题转化为证明 $f'(\xi) = \cfrac{f(b) - f(a)}{b - a} = 0$
做辅助函数 $\varphi(x) = f(x) - \cfrac{f(b) - f(a)}{b - a}x$
显然， $\varphi (x)$ 在 $[a, b]$ 上连续， 在 $(a, b)$ 内可导，且 $\varphi (a) = \cfrac{bf(a) - af(b)}{b - a} = \varphi(b)$，由罗尔定理已知至少存在一点 $\xi \in (a, b)$， 使 $\varphi(\xi) = 0$

拉格朗日中值定理的几何意义

拉格朗日中值定理说明了怎样的函数具有平行于 A、B 两点连线的切线。

推论1： 若函数 $f(x)$ 在区间 I 上满足 $f'(x) = 0$，则 $f(x)$ 在 I 上必为常数
推论2： 如果 $f(x)$ 和 $g(x)$ 在 $(a, b)$ 内可导，并且在 $(a, b)$ 内恒有 $f'(x) = g'(x)$，那么 $f(x) = g(x) + C, \forall x\in (a, b),$ 其中 C 为某个常数。

第二节 洛必达法则

一、洛必达法则定义

定理 4.4 洛必达法则

如果 $f(x)$ 和 $g(x)$ 满足系列条件：

1. $\lim \limits_{x \to a} f(x) = \lim \limits_{x \to a} g(x) = 0$ 或 $\infty$
2. 在点 $a$ 的某去心领域内， $f(x)$ 与 $g(x)$ 可导，且 $g(x) \neq 0$;
3. $\lim \limits_{x \to a} \cfrac{f'(x)}{g'(x)}$存在（或者 $\infty$）

所以 $\lim \limits_{x \to a} \cfrac{f(x)}{g(x)} = \lim \limits_{x \to a} \cfrac{f'(x)}{g'(x)}$

例题

1. $\lim \limits_{x \to 0} \cfrac {e ^ x - 1} {x}.$
   $\lim \limits_{x \to 0} \cfrac {e ^ x - 1} {x} = \lim \limits_{x \to 0} \cfrac {(e ^ x - 1)'} {(x)'} = \lim \limits_{x \to 0} \cfrac {e ^ x} {1} = 1$
2. $\lim \limits_{x \to \infty} \cfrac{\ln x}{x ^ a}.$
   $\lim \limits_{x \to \infty} \cfrac{\ln x}{x ^ a} = \lim \limits_{x \to \infty} \cfrac{(\ln x)'}{(x ^ a)'} = \lim \limits_{x \to \infty} \cfrac{\frac{1}{x}}{a x ^ {a - 1}} = \lim \limits_{x \to \infty} \cfrac{1}{ax ^ a} = 0$
3. $\lim \limits_{x \to 0} \cfrac {x - \sin x} {x ^ 3}.$
   $\lim \limits_{x \to 0} \cfrac {x - \sin x} {x ^ 3} = \lim \limits_{x \to 0} \cfrac {(x - \sin x)'} {(x ^ 3)'} = \lim \limits_{x \to 0} \cfrac {1 - \cos x} {3 x ^ 2} = \lim \limits_{x \to 0} \cfrac {(1 - \cos x)'} {(3 x ^ 2)'} = \lim \limits_{x \to 0} \cfrac {\sin x} {6x} = \cfrac {1}{6}$

总结，上述 $1$， $3$ 为 $0/0$ 型， $2$ 为 $\infty / \infty$ 型。

二、 其他类型的未定式子

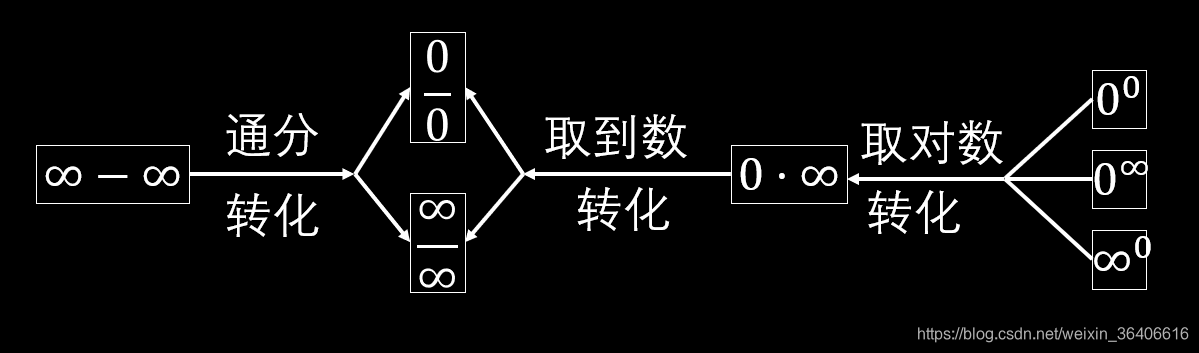
例题

1. $\lim \limits_{x \to 1}(\cfrac{x}{x - 1} - \cfrac{1}{\ln x})$
   $\lim \limits_{x \to 1}(\cfrac{x}{x - 1} - \cfrac{1}{\ln x}) = \lim \limits_{x \to 1}(\cfrac{x \ln x - (x - 1)}{\ln x (x - 1)}) = \lim \limits_{x \to 1}(\cfrac{(x \ln x - x + 1)'}{(x\ln x - \ln x)'}) = \lim \limits_{x \to 1}(\cfrac{\ln x}{(\ln x + 1 - \frac {1}{x})}) = \lim \limits_{x \to 1}(\cfrac{(x \ln x)'}{(x\ln x + x - 1)'}) = \lim \limits_{x \to 1}(\cfrac{\ln x + 1}{\ln x + 2}) = \cfrac 1 2$

第三节 函数的单调性

函数的单调性

定理 $4.5$ 设函数 $f(x)$ 在 $[a, b]$ 上连续，在 $(a, b)$ 内可导，

1. 如果在 $(a, b)$ 内 $f'(x) \gt 0$，那么函数 $f(x)$ 在 $[a, b]$ 上单调递增。
2. 如果在 $(a, b)$ 内 $f'(x) \lt 0$，那么函数 $f(x)$ 在 $[a, b]$ 上单调递减。

证明： $\forall x_1, x_2 \in [a, b],$ 设 $x_1 \lt x_2$， 由拉格朗日中值定理： $f(x_2) - f(x_1) = f'(\xi)(x_2 - x_1)$

例题

1. 讨论函数 $f(x) = 3x + x ^ 3$ 的单调性
   解：函数在定义域内连续并且 $f'(x) = 3 - 3 * x ^ 2 = 3(1 - x)(1 + x)$
   

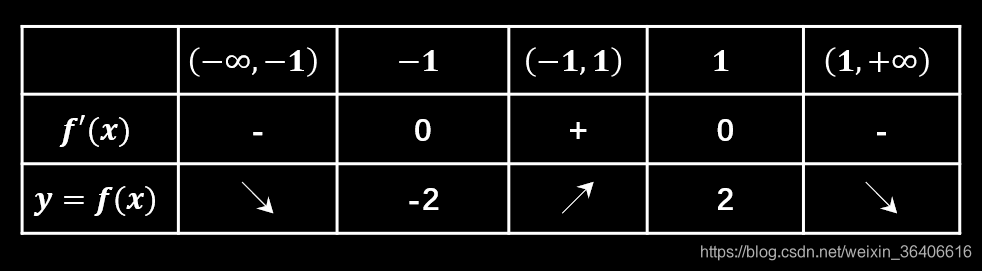
第四节 函数的极值及其求法

函数的极值

定理4.6 （必要条件） 如果 $x_0$ 是函数 $f(x)$ 的极值点， 则 $x_0$ 必为函数 $f(x)$ 的驻点 或 不可导点，亦即， $f'(x_0) = 0$ 或 $f'(x_0)$ 不存在。

函数极值的求法

定理 4.7 (第一充分条件)

设函数 $f(x)$ 在点 $x_0$ 的某领域 $(x_0 - \delta, x_0 + \delta)$ 内连续，在去心领域内可导

1. 如果 $x \in (x_0 - \delta, x_0)$ 时， $f'(x) \gt 0$； 当 $x \in (x_0, x_0 + \delta)$ 时， $f'(x) \lt 0$，那么函数 $f(x)$ 在 $x_0$ 处取得极大值。
2. 如果 $x \in (x_0 - \delta, x_0)$ 时， $f'(x) \lt 0$； 当 $x \in (x_0, x_0 + \delta)$ 时， $f'(x) \gt 0$，那么函数 $f(x)$ 在 $x_0$ 处取得极小值。
3. 如果当 $x \in (x_0 - \delta, x_0) \bigcup (x_0, x_0 + \delta)$ 时，恒有 $f'(x) \gt 0$，或恒有 $f'(x) \lt 0$； 那么函数 $f(x)$ 在 $x_0$ 处没有极值。

定理4.8 （第二充分条件）

设函数 $f(x)$ 在点 $x_0$ 的某领域 $(x_0 - \delta, x_0 + \delta)$ 内连续，存在二阶导数，并且 $f'(x_0) = 0, f''(x_0) \neq 0$

1. 若 $f''(x) \lt 0$，则函数 $y = f(x)$ 在 $x_0$ 处取得极大值；
2. 若 $f''(x) \lt 0$，则函数 $y = f(x)$ 在 $x_0$ 处取得极小值。

例题

1. 计算 $y = - x^4 + 2 x ^ 2$ 的极值
   解： $y' = -4x^ 3 + 4x = -4x(x - 1)(x + 1)$
   令 $y' = 0$ 时，则驻点为： $x_1 = -1, x_2 = 0, x_3 = 1$
   又 $y'' = -12 x^ 2 + 4$
   $y''(-1) = y''(1) = -8 \lt 0, y''(0) = 4 \gt 0$
   由定理 $4.8$ 判断， $x_1 = -1, x_3 = 1$ 处取得极大值 $1$， $x_2 = 1$处取得极小值 $0$.

第五节 函数的最大值和最小值及其应用

函数的最值

假定函数 $f(x)$ 在闭区间 $[a, b]$ 上连续，在开区间 $(a, b)$ 内最多有有限个驻点和导数不存在的点。则由上面的分析知，函数 $f(x)$在 $[a, b]$上的最大值和最小值要么在端点 $a, b$ 处达到，要么是极值，从而在某个极值点处达到。 而由极值的必要条件知， 极值点要么是驻点，要么是函数的不可导点。因此，函数 $f(x)$ 在 $[a, b]$ 上的最大值和最小值只可能在端点 $a,b,f(x)$ 的驻点，或者不可导点处取到，故只需要求出这些点处的函数值并加以比较：其中最大的即为最大值，最小的即为最小值。

具体归纳出来可以按一下步骤求满足上述条件的函数的极值：

1. 求出 $f(x)$ 在 $(a,b)$ 上的所有驻点和导数不存在的点；
2. 求出驻点，导数不存在的点以及端点的函数值；
3. 比较函数在端点、驻点、不可导点处的值，最大的即为最大值，最小的即为最小值。

第六节 函数的凹凸性和拐点

凹凸性的定义

设函数 $y = f(x)$ 在区间 $I$ 上连续。如果对任意的 $x_1, x_2 \in I$ 且 $x_1 \neq x_2$ 恒有 $f(\cfrac{x_1 + x_2}{2}) \lt \cfrac {f(x_1) + f(x_2)}{2}$，则称函数 $f(x)$ 的曲线在区间 $I$ 上是凹 的；如果恒有 $f(\cfrac{x_1 + x_2}{2}) \gt \cfrac {f(x_1) + f(x_2)}{2}$ 则称函数 $f(x)$ 的曲线在区间 $I$ 上是凸的；

函数的凹凸性

设函数 $f(x)$ 在闭区间 $[a, b]$ 上连续，在 $(a, b)$ 内具有二阶导数。

1. 若在 $(a,b)$ 内 $f''(x) \gt 0$，则函数 $f(x)$ 在 $[a,b]$ 上的曲线是凹的；
2. 若在 $(a,b)$ 内 $f''(x) \lt 0$，则函数 $f(x)$ 在 $[a,b]$ 上的曲线是凸的；

拐点

连续函数 $f(x)$ 的图像上的凹凸性的分界点称为函数的拐点
按以下步骤求函数的拐点以及凹凸区间：

1. 求 $f''(x)$ ，并求出在所讨论区间内的 $f''(x)$ 不存在的点；
2. 求 $f''(x) = 0$， 求出位于所讨论区间的所有实根；
3. 讨论 $f''(x)$ 在以上求出的区间内 $f''(x) = 0$ 的点以及 $f''(x)$ 不存在的点的左右两侧的符号，确定该点是否为拐点。