第三章 微分中值定理与导数的应用

习题3-1 微分中值定理

我们先讲罗尔（Rolle）定理，然后根据它推出拉格朗日（Lagrange）中值定理和柯西（Cauchy）中值定理。——高等数学同济版

  本节主要讲述微分中值定理及其证明，习题以证明题为主。

6.证明恒等式： $\arcsin x+arccos x=\cfrac{\pi}{2}(-1\leqslant x\leqslant1).$

解  取函数 $f(x)=\arcsin x+arccos x,x\in[-1,1]$。因
$f'(x)=\cfrac{1}{\sqrt{1-x^2}}-\cfrac{1}{\sqrt{1-x^2}}\equiv0,$
  故 $f(x)\equiv0$。取 $x=0$，得 $f(0)=C=\cfrac{\pi}{2}$。因此
$\arcsin x+arccos x=\cfrac{\pi}{2},\qquad x\in[-1,1].$
（证明不等式首先构造函数，利用函数求解）

13.设 $f(x),g(x)$在 $[a,b]$上连续，在 $(a,b)$内可导，证明在 $(a,b)$内有一点 $\xi$，使 $\begin{vmatrix}f(a)&f(b)\\g(a)&g(b)\end{vmatrix}=(b-a)\begin{vmatrix}f(a)&f'(\xi)\\g(a)&g'(\xi)\end{vmatrix}.$

解  取函数 $F(x)=\begin{vmatrix}f(a)&f(x)\\g(a)&g(x)\end{vmatrix}$，由 $f(x),g(x)$在 $[a,b]$上连续，在 $(a,b)$内可导知 $F(x)$在 $[a,b]$上连续，在 $(a,b)$内可导，由拉格朗日中值定理知，至少存在一点 $\xi\in(a,b)$，使 $F(a)-F(b)=F'(\xi)(b-a)$。即
$F(b)=\begin{vmatrix}f(a)&f(b)\\g(a)&g(b)\end{vmatrix},\quad F(a)=\begin{vmatrix}f(a)&f(a)\\g(a)&g(a)\end{vmatrix}\\ F'(x)=\begin{vmatrix}f(0)&f(x)\\g(0)&g(x)\end{vmatrix}+\begin{vmatrix}f(a)&f'(x)\\g(a)&g'(x)\end{vmatrix}=\begin{vmatrix}f(a)&f'(x)\\g(a)&g'(x)\end{vmatrix},$
  故
$\begin{vmatrix}f(a)&f(b)\\g(a)&g(b)\end{vmatrix}=\begin{vmatrix}f(a)&f'(\xi)\\g(a)&g'(\xi)\end{vmatrix}(b-a).$
（利用行列式求导法则求导，当函数 $f(x)=\begin{vmatrix} f_{11}(x)&f_{12}(x)&\cdots&f_{1n}(x)\\ f_{21}(x)&f_{22}(x)&\cdots&f_{2n}(x)\\ \vdots&\vdots& &\vdots\\ f_{n1}(x)&f_{n2}(x)&\cdots&f_{nn}(x)\\ \end{vmatrix}$时， $f'(x)=\overset{n}{\underset{i=1}{\sum}}\begin{vmatrix} f_{11}(x)&f_{12}(x)&\cdots&f_{1n}(x)\\ \vdots&\vdots & &\vdots\\ f'_{i1}(x)&f'_{i2}(x)&\cdots&f'_{in}(x)\\ \vdots&\vdots&&\vdots\\ f_{n1}(x)&f_{n2}(x)&\cdots&f_{nn}(x)\\ \end{vmatrix}$或 $f‘(x)=\overset{n}{\underset{i=1}{\sum}}\begin{vmatrix} f_{11}(x)&\cdots&f'_{1i}(x)&\cdots&f_{1n}(x)\\ f_{21}(x)&\cdots&f'_{2i}(x)&\cdots&f_{2n}(x)\\ \vdots&\vdots& &\vdots\\ f_{n1}(x)&\cdots&f'_{ni}(x)&\cdots&f_{nn}(x)\\ \end{vmatrix}$）

14.证明：若函数 $f(x)$在 $(-\infty,+\infty)$内满足关系式 $f'(x)=f(x)$，且 $f(0)=1$，则 $f(x)=e^x$。

解  取函数 $F(x)=\cfrac{f(x)}{e^x}$，因
$F'(x)=\cfrac{f'(x)e^x-f(x)e^x}{e^{2x}}=\cfrac{f'(x)-f(x)}{e^x}=0.$
  故 $F(x)=C$。又 $F(x)=C=f(0)=1$，因此 $F(x)=1$，即 $\cfrac{f(x)}{e^x}=1$，故 $f(x)=e^x$。
（构造函数使函数恒等于常数，再证明函数成立）

15.设函数 $y=f(x)$在 $x=0$的某邻域内具有 $n$导数，且 $f(0)=f'(0)=\cdots=f^{(n-1)}(0)=0$，试用柯西中值定理证明： $\cfrac{f(x)}{x^n}=\cfrac{f^{(n)}(\theta x)}{n!}\qquad(0<\theta<1).$

解  已知 $f(x)$在 $x=0$的某邻域内具有 $n$导数，在该邻域内任取点 $x$，由柯西中值定理得
$\cfrac{f(x)}{x^n}=\cfrac{f(x)-f(0)}{x^n-0^n}=\cfrac{f'(\xi_1)}{n\xi^{n-1}_1},$
  其中 $\xi_1$介于 $0,x$之间。又
$\cfrac{f'(\xi_1)}{n\xi^{n-1}_1}=\cfrac{f'(\xi_1)-f'(0)}{n(\xi^{n-1}_1-0^{n-1})}=\cfrac{f''(\xi_2)}{n(n-1)\xi^{n-2}_2},$
  其中 $\xi_2$介于 $0,\xi_1$之间。依此类推，得
$\cfrac{f^{(n-1)}(\xi_{n-1})}{n!\xi_{n-1}}=\cfrac{f^{(n-1)}(\xi_{n-1})-f^{(n-1)}(0)}{n!(\xi_{n-1}-0)}=\cfrac{f^{(n)}(\xi_n)}{n!},$
  其中 $\xi_n$介于 $0,\xi_{n-1}$之间，记 $\xi_n=\theta x(0<\theta<1)$，因此
$\cfrac{f(x)}{x^n}=\cfrac{f^{(n)}(\xi_n)}{n!}=\cfrac{f^{(n)}(\theta x)}{n!}\quad(0<\theta<1).$
（利用柯西中值定理逐阶推导至一般规律）

习题3-2 洛必达法则

  本节主要介绍洛必达法则及其应用。

1.用洛必达法则求下列极限：

（12） $\lim\limits_{x\to0}x^2e^{\frac{1}{x^2}};$

解
$\lim\limits_{x\to0}x^2e^{\frac{1}{x^2}}=\lim\limits_{x\to0}\cfrac{e^{\frac{1}{x^2}}}{\cfrac{1}{x^2}}=\lim\limits_{x\to0}\cfrac{e^{\frac{1}{x^2}}\left(\cfrac{1}{x^2}\right)'}{\left(\cfrac{1}{x^2}\right)'}=\lim\limits_{x\to0}e^{\frac{1}{x^2}}=+\infty.$
（求解该极限时先构造可以用洛必达法则求解的形式，对于相同的部分抵消）

（14） $\lim\limits_{x\to\infty}\left(1+\cfrac{a}{x}\right)^x;$

解   $\lim\limits_{x\to\infty}\left(1+\cfrac{a}{x}\right)^x=e^{\lim\limits_{x\to\infty}x\ln\left(1+\cfrac{a}{x}\right)}$，而
$\lim\limits_{x\to\infty}x\ln\left(1+\cfrac{a}{x}\right)=\lim\limits_{x\to\infty}\cfrac{\ln\left(1+\cfrac{a}{x}\right)}{\cfrac{1}{x}}=\lim\limits_{x\to\infty}\cfrac{\cfrac{1}{1+\cfrac{a}{x}}\cdot\left(-\cfrac{a}{x^2}\right)}{-\cfrac{1}{x^2}}=\lim\limits_{x\to\infty}\cfrac{a}{1+\cfrac{a}{x}}=a.$
  故 $\lim\limits_{x\to\infty}\left(1+\cfrac{a}{x}\right)^x=e^a$。（这道题将指数中的变量转移，使之构造成可以使用洛必达法则的形式）

（15） $\lim\limits_{x\to0^+}x^{\sin x};$

解   $\lim\limits_{x\to0^+}x^{\sin x}=e^{\lim\limits_{x\to0^+}\sin x\ln x}$，而
$\lim\limits_{x\to0^+}\sin x\ln x=\lim\limits_{x\to0^+}\cfrac{\sin x}{x}\cdot\cfrac{\ln x}{\cfrac{1}{x}}=\lim\limits_{x\to0^+}\cfrac{\cfrac{1}{x}}{-\cfrac{1}{x^2}}=\lim\limits_{x\to0^+}(-x)=0,$
  故 $\lim\limits_{x\to0^+}x^{\sin x}=e^0=1$（这道题同（14）题）

（16） $\lim\limits_{x\to0^+}\left(\cfrac{1}{x}\right)^{\tan x}.$

解
$\lim\limits_{x\to0^+}\left(\cfrac{1}{x}\right)^{\tan x}=e^{\lim\limits_{x\to0^+}\tan x\ln\cfrac{1}{x}}=e^{\lim\limits_{x\to0^+}\frac{\tan x}{x}\cdot\frac{-\ln x}{\frac{1}{x}}}=e^{\lim\limits_{x\to0^+}\cfrac{-\frac{1}{x}}{-\frac{1}{x^2}}}=e^{\lim\limits_{x\to0^+}x}=e^0=1.$
（这道题同（14）题）

4.讨论函数 $f(x)=\begin{cases}\left[\cfrac{(1+x)^{\frac{1}{x}}}{e}\right]^{\frac{1}{x}},&x>0,\\e^{-\frac{1}{2}},&x\leqslant0\end{cases}$在点 $x=0$处的连续性。

解
$\lim\limits_{x\to0^+}f(x)=\lim\limits_{x\to0^+}\left[\cfrac{(1+x)^{\frac{1}{x}}}{e}\right]^{\frac{1}{x}}=e^{\lim\limits_{x\to0^+}\frac{1}{x}\ln\left[\frac{(1+x)^{\frac{1}{x}}}{e}\right]},$
  而
$\begin{aligned} \lim\limits_{x\to0^+}\frac{1}{x}\left[\frac{1}{x}\ln(1+x)-1\right]&=\lim\limits_{x\to0^+}\cfrac{\ln(x+1)-x}{x^2}=\lim\limits_{x\to0^+}\cfrac{\cfrac{1}{1+x}-1}{2x}\\&=\lim\limits_{x\to0^+}-\cfrac{1}{2(1+x)}=-\cfrac{1}{2},\end{aligned}$
  故
$\lim\limits_{x\to0^+}f(x)=e^{-\frac{1}{2}},$
  又
$\lim\limits_{x\to0^-}f(x)=\lim\limits_{x\to0^-}e^{-\frac{1}{2}}=e^{-\frac{1}{2}},f(0)=e^{-\frac{1}{2}}.$
  因为 $\lim\limits_{x\to0^+}f(x)=\lim\limits_{x\to0^-}f(x)=f(0)$，故函数 $f(x)$在 $x=0$处连续。（这道题同1.（14）题）

习题3-3 泰勒公式

  本节主要介绍泰勒公式及其应用。

10.利用泰勒公式求下列极限：

（1） $\lim\limits_{x\to+\infty}(\sqrt[3]{x^3+3x^2}-\sqrt[4]{x^4-2x^3})$

解
$\begin{aligned}\lim\limits_{x\to+\infty}(\sqrt[3]{x^3+3x^2}-\sqrt[4]{x^4-2x^3})&=\lim\limits_{x\to+\infty}x\left[\left(1+\cfrac{3}{x}\right)^{\cfrac{1}{3}}-\left(1-\cfrac{2}{x}\right)^{\cfrac{1}{4}}\right]\\ &=\lim\limits_{x\to+\infty}x\left[1+\cfrac{1}{3}\cdot\cfrac{3}{x}+\omicron\left(\cfrac{1}{x}\right)-1+\cfrac{1}{4}\cdot\cfrac{2}{x}+\omicron\left(\cfrac{1}{x}\right)\right]\\&=\lim\limits_{x\to+\infty}\left[\cfrac{3}{2}+\cfrac{\omicron\left(\cfrac{1}{x}\right)}{\cfrac{1}{x}}\right]=\cfrac{3}{2}.\end{aligned}$
（这道题主要利用泰勒公式展开化简）

习题3-4 函数的单调性与曲线的凹凸性

  本节主要介绍了函数单调性的判断、拐点的判断和凹凸性的判断。

习题3-5 函数的极值与最大值最小值

  本节主要介绍函数的极值与最大值最小值的求法。

4.设函数 $f(x)$在 $x_0$处有 $n$阶导数，且 $f'(x_0)=f''(x_0)=\cdots=f^{(n-1)}(x_0)=0$， $f^{(n)}(x_0)\ne0$，证明：

（1）当 $n$为奇数时， $f(x)$在 $x_0$处不取得极值；

证  由含佩亚诺余项的 $n$阶泰勒公式及已知条件，得
$f(x)=f(x_0)+\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+\omicron\left((x-x_0)^n\right),$
  即 $f(x)-f(x_0)=\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n+\omicron\left((x-x_0)^n\right)$，由此式可知 $f(x)-f(x_0)$在 $x_0$某邻域内的符号由 $\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n$在 $x_0$某邻域内的符号决定。
  （1）当 $n$为奇数时， $(x-x_0)^n$在 $x_0$两侧异号，所以 $\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n$在 $x_0$两侧异号，从而 $f(x)-f(x_0)$在 $x_0$两侧异号，故 $f(x)$在 $x_0$处不取得极值。

（2）当 $n$为偶数时， $f(x)$在 $x_0$处取得极值，且当 $f^{(n)}(x_0)<0$时， $f(x)$为极大值，当 $f^{(n)}(x_0)>0$时， $f(x)$为极小值。

证  （2）当 $n$为偶数时，在 $x_0$两侧 $(x-x_0)^n>0$，若 $f^{(n)}(x_0)<0$，则 $\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n<0$，从而 $f(x)-f(x_0)<0$，即 $f(x)<f(x_0)$，故 $f(x)$为极大值；若 $f^{(n)}(x_0)>0$，则 $\cfrac{f^{(n)}(x_0)}{n!}(x-x_0)^n>0$，从而 $f(x)-f(x_0)>0$，即 $f(x)>f(x_0)$，故 $f(x)$为极小值。
（这道题是导数和泰勒公式的综合应用）

习题3-6 函数图形的描绘

  本节主要介绍函数画图的方法，该部分作为考纲一部分内容，但实际考可能不多。（我猜的，没有任何依据） 步骤记录如下：

1. 确定函数 $f(x)$的定义域及函数所具有的某些特性（如奇偶性、周期性等），并求出函数的一阶导数 $f'(x)$和二阶导数 $f''(x)$;
2. 求出一阶导数 $f'(x)$和二阶导数 $f''(x)$的全部零点，并求出函数 $f(x)$的间断点及 $f'(x)$和 $f''(x)$不存在的点，用这些点把函数的定义域划分成几个部分区间；
3. 确定这些部分区间内 $f'(x)$和 $f''(x)$的符号，并由此确定函数图形的升降、凹凸和拐点；
4. 确定函数图形的水平、铅直渐近线以及其他变化趋势；
5. 算出 $f'(x)$和 $f''(x)$的零点以及不存在的点所对应的函数值，定出图形上相对应的点；为了把图形描绘得准确些，有时还需要补充一些点，然后结合第三四步中得到的结果，联结这些点画出函数 $y=f(x)$的图形。——高等数学同济版

习题3-7 曲率

  本节主要介绍弧微分、曲率、曲率圆、曲率半径及其计算公式。书中提及的曲率中心及渐曲线与渐伸线没有在考纲中明确提及。

曲率
$K=\cfrac{|y''|}{\left(1+y'^2\right)^{\frac{3}{2}}}$
曲率半径
$\rho=\cfrac{1}{K}$

习题3-8 方程的近似解

  本节主要介绍了方程的近似解的求法（包括二分法、切线法和割线法），但在考纲中并未提及该节。

总习题三

3.列举一个函数 $f(x)$满足 $f(x)$在 $[a,b]$上连续，在 $(a,b)$内除了某一点处处可导，但在 $(a,b)$内不存在点 $\xi$，使 $f(b)-f(a)=f'(\xi)(b-a)$。

解  取 $f(x)=|x|$，区间为 $[-1,1]$。函数 $f(x)$在 $[-1,1]$上连续，在 $(-1,1)$内除点 $x=0$外处处可导，但 $f(x)$在 $(-1,1)$内不存在点 $\xi$，使 $f'(\xi)=0$，即不存在 $\xi\in(-1,1)$，使 $f(1)-f(-1)=f'(\xi)[1-(-1)]$。（这个函数比较难以想到，该情况多出现在分段函数中）

6.设 $a_0+\cfrac{a_1}{2}+\cdots+\cfrac{a_n}{n+1}=0$，证明多项式 $f(x)=a_0+a_1x+\cdots+a_nx^n$在 $(0,1)$内至少有一个零点。

证  取函数 $F(x)=a_0x+\cfrac{a_1}{2}x^2+\cdots+\cfrac{a_n}{n+1}x^{n+1}$。 $F(x)$在 $[0,1]$上连续，在 $(0,1)$内可导，且 $F(0)=0,F(1)=a_0+\cfrac{a_1}{2}+\cdots+\cfrac{a_n}{n+1}=0$，由罗尔定理知至少存在一点 $\xi\in(-1,1)$，使 $F'(\xi)=0$，即多项式 $f(x)=a_0+a_1x+\cdots+a_nx^n$在 $(0,1)$内至少有一个零点。（这道题难点主要在构造函数）

8.设 $0<a<b$,函数 $f(x)$满足 $f(x)$在 $[a,b]$上连续，在 $(a,b)$内可导，试利用柯西中值定理，证明存在一点 $\xi\in(a,b)$，使 $f(b)-f(a)=\xi f'(\xi)\ln\cfrac{b}{a}.$

证  取函数 $F(x)=\ln x$， $f(x)$、 $F(x)$在 $[a,b]$上连续，在 $(a,b)$内可导，且 $F'(x)=\cfrac{1}{x}\ne0,x\in(a,b)$。由柯西中值定理知至少存在一点 $\xi\in(a,b)$，使
$\cfrac{f(b)-f(a)}{F(b)-F(a)}=\cfrac{f'(\xi)}{F'(\xi)}.$
  即 $\cfrac{f(b)-f(a)}{\ln b-\ln a}=\cfrac{f'(\xi)}{\cfrac{1}{\xi}}.$
  亦即 $f(b)-f(a)=\xi f'(\xi)\ln\cfrac{b}{a}$。（这道题主要考察构造函数以及等式变换）

9.设 $f(x),g(x)$都是可导函数，且 $|f'(x)|<g'(x)$，证明：当 $x>a$时， $|f(x)-f(a)|<g(x)-g(a).$

证  取 $F(x)=f(x)-g(x),G(x)=f(x)+g(x),x\in(a,+\infty)$。由 $|f'(x)|<g'(x)$知
$f'(x)-g'(x)<0,\qquad f'(x)+g'(x)>0,$
  故 $F'(x)=f'(x)-g'(x)<0,G'(x)=f'(x)+g'(x)>0$，即当 $x>a$时，函数 $F(x)$单调减少， $G(x)$单调增加。因此
$F(x)<F(a),\qquad G(x)>G(a)(x>a).$
  从而
$f(x)-g(x)<f(a)-g(a),f(x)+g(x)>f(a)+g(a)\qquad(x>a).$
  即当 $x>a$时， $|f(x)-f(a)|<g(x)-g(a).$（这道题主要考察绝对值的不等式展开）

13.设 $a>1$， $f(x)=a^x-ax$在 $(-\infty,+\infty)$内的驻点为 $x(a)$。问 $a$为何值时， $x(a)$最小？并求出最小值。

解  由 $f'(x)=a^x\ln a-a=0$，得唯一驻点
$x(a)=1-\cfrac{\ln\ln a}{\ln a}.$
  考察函数 $x(a)=1-\cfrac{\ln\ln a}{\ln a}$在 $a>1$时的最小值。令
$x'(a)=-\cfrac{\cfrac{1}{a}-\cfrac{1}{a}\ln\ln a}{(\ln a)^2}=-\cfrac{1-\ln\ln a}{a(\ln a)^2}=0,$
得唯一驻点， $a=e^e$。当 $a>e^e$时， $x'(a)>0$；当 $a<e^e$时， $x'(a)<0$，因此
$x(e^e)=1-\cfrac{1}{e}$
为极小值，也是最小值。（在对 $x(a)$求导时，注意在 $a$在底数和真数中，求导时要注意）

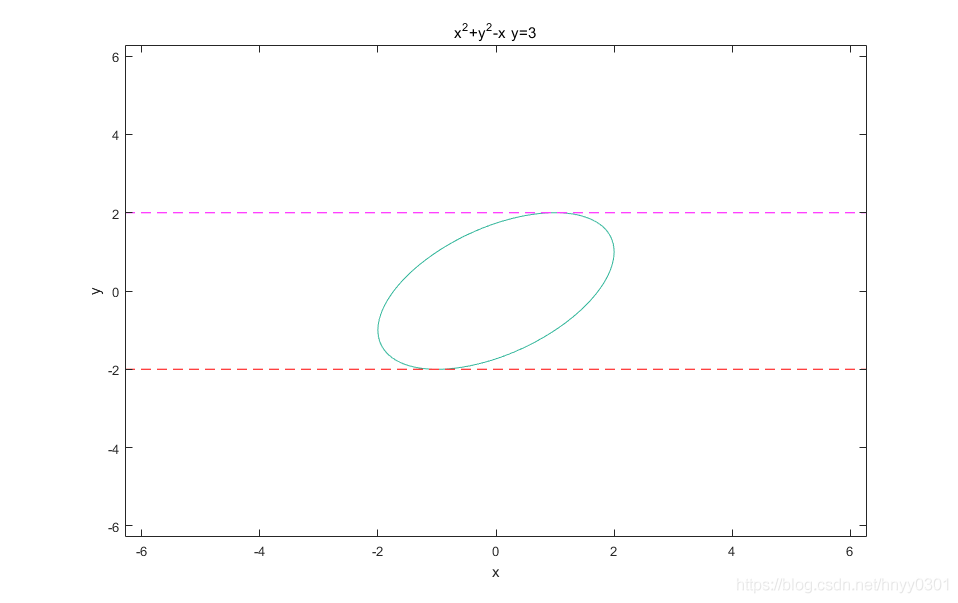
14.求椭圆 $x^2-xy+y^2=0$上纵坐标最大和最小的点。

解  在椭圆方程两端分别对 $x$求导，得
$2x-y-xy'+2yy'=0,\\ y'=\cfrac{y-2x}{2y-x}.$
  令 $y'=0$，得 $y=2x$。将 $y=2x$代入椭圆方程后得 $x^2=1$，故 $x=\pm1$。从而得到椭圆上的点 $(1,2),(-1,-2)$。根据题意即知点 $(1,2),(-1,-2)$为椭圆 $x^2-xy+y^2=0$上纵坐标最大和最小的点。（这道题需要仔细审题，题目中明确说明函数形状为椭圆，根据几何知识可知，在椭圆上纵坐标最大和最小的点处极值为0。函数图形和纵坐标最大和最小的点处的切线如下图所示）

20.试确定常数 $a$和 $b$，使 $f(x)=x-(a+b\cos x)\sin x$为当 $x\to0$时关于 $x$的5阶无穷小。

解  利用泰勒公式
$\begin{aligned} f(x)&=x-a\sin x-\cfrac{b}{2}\sin2x\\ &=x-a\left[x-\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\omicron(x^5)\right]-\cfrac{b}{2}\left[2x-\cfrac{(2x)^3}{3!}+\cfrac{(2x)^5}{5!}\omicron(x^5)\right]\\ &=(1-a-b)x+\left(\cfrac{a}{6}+\cfrac{2b}{3}\right)x^3-\left(\cfrac{a}{120}+\cfrac{2b}{15}\right)x^5+\omicron(x^5). \end{aligned}$
  按题意，应有
$\begin{cases} 1-a-b=0,\\ \cfrac{a}{6}+\cfrac{2b}{3}=0,\\ \cfrac{a}{120}+\cfrac{2b}{15}\ne0, \end{cases}$
得 $a=\cfrac{4}{3},b=-\cfrac{1}{3}$。因此，当 $a=\cfrac{4}{3},b=-\cfrac{1}{3}$时， $f(x)=x-(a+b\cos x)\sin x$是当 $x\to0$时关于 $x$的5阶无穷小。（这道题主要考察三角函数的泰勒展开式）

写在最后

  如果觉得文章不错就点个赞吧。另外，如果有不同的观点，欢迎留言或私信。
   欢迎非商业转载，转载请注明出处。