我一直坚信,学一个课程要把整个内容融会贯通起来,要用出题人的思维去解决题目,当一道题摆到你面前的时候你应该有一种或多种思考角度,然后逐一尝试来解决题目,而不是左右摇摆。
上一章已经介绍了导数与微分,那么很明显,第三章就是要熟悉微分熟悉导数,并能够知道它们可以做些什么。
首先第一节带领我们了解微分中值定理。
什么是微分中值定理,每一个数学名词都有它之所以这么叫的原因,微分,中值?中间值?这些定理之间又有什么联系呢。
一、微分中值定理
1.1 罗尔定理
其实课本先讲述了费马引理,自然是为了引出后面的罗尔定理。
费马引理 设函数fx在点x0的某邻域U(x0)内有定义,并且在x0处可导,如果对任意的x∈U(x0)有
fx<=fx0 (或者 fx>=fx0)
那么 f'x0=0
费马引理其实可以“凭感觉知道是对的”,但数学是一门严谨的科目,定理都是需要反复推敲并证明的。
费马引理的证明很简单,既然定理这么说了,那么设一个△x,f(△x+x)肯定<=f(x)(或者>=f(x))但是△x可能是负的也可能是正的,这样的话x0点的左右导数分别大于等于0,小于等于0(或者相反),那么根据可导的条件,左右导数必然相等,故f'(x0)=0
好,下面是罗尔定理,课本的定义我还是搬出来吧:
(1)在闭区间[a,b]上连续
(2)在开区间(a,b)内可导
(3)在区间端点处的函数值相等,即f(a)=f(b),那么在(a,b)内至少有一点ξ(a<ξ<b),使得f'(ξ)=0
前两个条件简记为闭区间连续开区间可导,至于端点处函数值相等,也很好记。
这个定理和费马引理一样,看上去就感觉应该是对的,
下面模拟大脑过程,
这个罗尔定理中函数的形状就好像是一座桥或者是一个盆地,两边平齐,那么总有一个最低点或者最高点使得这个导数为0。
看见没!重点来了,你自己其实在脑子里已经证明了罗尔定理!!但是你只是把它形象化了,并没有用数学语言呈现出来。注意
你刚才模拟过程中的一个词,最低点,最高点!这其实就是指这个函数的最大值,最小值,你的大脑已经在指明了考虑方向。罗尔定理只是说导数为零,可是你就想到了最高点。
那么我们就来用数学思维证明这个问题,
①你只是说函数两边平齐,你可没说这个函数一定是桥的形状或者是盆地,还可能是平地呢!对!所以第一种可能就是fx=常数,那么不用想也知道,开区间里的任意一个ξ都可以使得其导数为0
②桥或者盆地形状,那么我们以桥为例子,首先他的最高点是一定存在的对吧!然后因为是桥形,所以最高点肯定是异于a,b的,那么你想到了什么!根据最高点可以推出导数为0??你想到了什么,当然是费马引理啦!这就是开头引出费马引理的原因吧。
如果有多个最大值最小值很明显就有多个ξ使之成立喽!
1.2拉格朗日中值定理
我们注意到,罗尔定理其实还是有一个条件限制的,那就是fa=fb,这是一个很奇怪的条件,为什么要两边相等?拉格朗日提出了疑问,他开始尝试去解释或者说去尝试去掉这个条件,会变成什么样子。

是的,会变成这个样子,给人一种倾斜的感觉,其实罗尔定理只是把它摆正了,摆正只不过是倾斜的一种方式!所以,很明显,罗尔定理只是拉格朗日定理的一种特殊情况!
拉格朗日为了载入史册,于是提出了拉格朗日定理:
保留罗尔定理的前两个条件,即闭区间连续,开区间可导,直接得出结论,在ab之间必然有一点ξ
使得等式f(b)-f(a)=f'(ξ)(b-a)成立,over
很不幸的是,这个好看的一个式子,因为出题人的存在,而变得变化多端,是的,下面的式子都是此等式的其他形式:
f(x+△x)-f(x)=f'(ξ)△x
f(x+△x)-f(x)=f'(x+θ*△x)△x,0<θ<1
是的,ξ是介于a,b之间的,一定要记住这一点。
哎,这个拉格朗日也是个聪明人,知道既然自己的定理和罗尔同学的定理很像,所以肯定也是利用罗尔定理来证明自己的牛逼定理,可是不满足人家罗尔的端点值相等的条件啊,
拉格朗日心一横,再创建一个辅助函数吧!只要这个φ函数满足罗尔定理不就好了嘛。可是这个辅助函数怎么找呢?
这个辅助函数不好找啊,但是拉格朗日这个老狐狸还是很聪明的,你想这个辅助函数其实是包含自己的那一套拉格朗日理论的,但是他又是对于罗尔定理成立的,感觉满足罗尔定理还得和自己有关系,应该是在几何中隐藏着那么一个函数的,它的存在就是相当于一种必然的联系,毕竟罗尔定理只是拉格朗日定理的一种情况而已。

对,就是MN线段(即曲线到ab直线的距离),把他表示为φx,很明显当x等于a,b时这个线段的长度为0,可将值是相等的。
知道MN的含义是曲线到ab直线的距离我们就明白怎么用函数来表示出MN这个φx了。
φx=曲线(x)-L(x),L为ab直线方程
太简单了,直接写出来就好了
φx=f(x)-L(x)=f(x)-f(a)-(f(b)-f(a))(x-a)/(b-a)
后面就水到渠成了,不赘述了

至此,拉格朗日同学让罗尔颜面扫地。
但是拉格朗日定理的作用还远不止与此,我们回过头来看这个公式
f(x+△x)-f(x)=f'(x+θ*△x)△x,0<θ<1
你看他像不像
△y=f'(x+θ*△x)△x
嗯,好吧,罗尔心服口服了。
我们知道函数的微分dy=f'(x)△x是函数的增量△y的近似表达式,一般来说用dy代替△y的误差只有在△x趋于0时才趋于0,而上面那个式子竟然直接给出了自变量取得有限增量△x时,函数增量△y的准确表达式!因此这个定理也叫作有限增量定理,牛逼!上面那个式子也叫有限增量公式。
我们来看一下它的几何意义是啥:

不用多说什么了吧!
课本129页还说了一个定理,如果函数fx在区间I上连续,I内可导且导数恒为0,那么fx在区间I上是一个常数,
用拉格朗日定理可以证明之。
1.3柯西中值定理
罗尔同学不甘失败,叫上了同样刁钻的柯西同学来帮他报仇,柯西心思着拉格朗日都把定理写的这么涵盖范围这么大了,自己怎么才能钻空子呢!涵盖范围越大,其实可以钻空子的地方也越大。
柯西瞄准了参数方程!这么一种比较奇葩的方程。

是的,柯西把参数方程的拉格朗日形式表示了出来,然后感觉这个形状看上去和拉格朗日挺不一样的,是不是可以得出更加一般的一般性结论呢?
是的, 他做到了,柯西这个混蛋做到了。

其实我刚开始看柯西定理有些不太明白,上面这个式子不就是拉格朗日定理对于参数方程的一种表示形式嘛,为啥还可以推广出去???
这就是柯西的厉害之处了。
参数方程是一种什么方程?x和y是个强盗,他们俩的曲线是由他们俩的xy坐标点组成了,也就是说这个参数方程的曲线其实就是一堆xy的值凑成的坐标点连起来的曲线,而可恶的是,这些xy的值是通过掠夺人家正正规规的普通方程t的方程来得到的。x和y的值可是人家的函数值啊!也就是说其实这个参数方程是对应着两条普通的关于t的曲线的!
也就是说,柯西定理把两条关于t的曲线进行了整理,他不是像罗尔和拉格朗日一样针对一条曲线,他通过参数方程找到了两条曲线的规律。尽管还不清楚这样研究两条曲线有什么卵用。那如果罗尔定理和拉格朗日定理可以推广到三维空间,其实研究三条线也没问题。
之于柯西定理的证明则是很明显要依赖前面的定理的,我们观察到柯西定理有导数参与,那么我们想到设立一个辅助函数
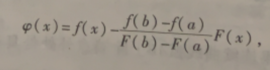
只要证明其导数=0即可,证明导数等于0我们很容易想到罗尔定理。关键的就是看φa是否=φb了。
经过计算是的。
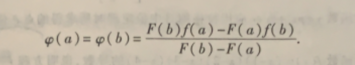
而且根据柯西定理的假设F'x是不会等于0的,那么自然F(b)-F(a)也不可能=0,于是乎我们就设置上面的辅助函数来验证罗尔定理了。
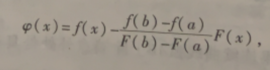
这个函数在闭区间连续,开区间可导,那么就没有异议了。

我其实对于柯西定理有些不知所错,不知道能用来干嘛,但是我思考了一下出题的角度,出题人应该就喜欢考柯西定理,毕竟可以只给你一个函数,然后让你构造出零一个函数来塑造成上面那种形式。我也上网看了一些人的评论,比如下面这个,我觉得挺好的。

https://zhidao.baidu.com/question/1373193559024260739.html 侵删
