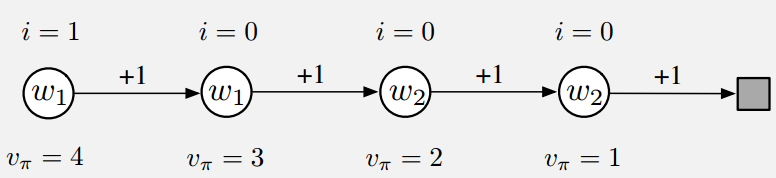[归纳]强化学习导论 - 第九章：基于拟合器的on-policy预测

1.本章内容概要

这一章，我们考虑用函数拟合器来估计on-policy RL中的state-value函数，即从经验中估计给定策略 $\pi$的值函数 $v_\pi$。本章新颖之处在于用函数(线性函数、人工神经网络、决策树等)来代替前几章一直使用的表格，函数的参数为 $\textbf{w}$，通常 $|\textbf{w}|<<|S|$，因此我们只需要少量参数，就能表征所有状态的值。通过调整 $\textbf{w}$，可以逼近经验，同时泛化到类似的状态。泛化性使得learning更加有效，同时也更难处理和理解。

在RL中引入函数拟合器，可能使RL在只部分可观测(states)问题中也可应用(自动学习状态空间的相关性和无关性)。实际上，本Part介绍的所有使用函数估计器的理论结果都能很好地应用到部分可观测问题中，函数估计器不能做的是无法通过观测的数据增强状态表征，而这在17章会深入讨论。

2.值函数拟合器

RL的所有prediction方法都是向着"backed-up value/update target"更新的过程 $s\mapsto u$，我们用 $u$表示update target，我们可以写出MC、TD(0)、n-step TD和DP的更新符号化表述，与前几章的区别在于bootstrapping所用的后续状态的值也由拟合器得来：

MC: $S_{t} \mapsto G_t$
TD(0): $S_{t} \mapsto R_{t+1}+\gamma \hat{v}\left(S_{t+1}, \mathbf{w}_{t}\right)$
n-step TD: $S_{t} \mapsto G_{t : t+n}$
DP: $s \mapsto \mathbb{E}_{\pi}\left[R_{t+1}+\gamma \hat{v}\left(S_{t+1}, \mathbf{w}_{t}\right) | S_{t}=s\right]$

每个update可以理解为值函数的期望输入(input)-输出(output)行为的一个例子(样本)，我们希望s的估计值接近于u。表格化的方法是只让s的值向u变动，而保持其它状态的值不变；而用拟合器的话实际上会导致相近状态的值一起变化(泛化)。机器学习(ML)中学习模仿input-output样例的方法叫做监督学习，如果输出是数值的则叫做函数拟合。

在拟合RL中，每个 $s\mapsto u$都是一个样例。因此，我们可以利用任何监督学习的方法。但是RL中的函数拟合器又有特殊性：为了保证能online工作，必须能从数据中高效地增量式学习；且要求函数拟合器能处理非平稳目标函数(因为对于基于GPI的control方法 $\pi$是一直在变化的，即使 $\pi$不发生变化，bootstrapping方法也会导致非平稳性)。

3.预测目标VE

在表格化方法中，各个状态的值之间是解耦的，相互之间无关，但是在拟合RL中，对一个状态的跟新也会影响到其它状态的值，因此无法保证所有状态的值都是精确的，这主要是因为 $|\textbf{w}|<<|s|$的特点。因此我们需要关注那些更重要的状态，我们用 $\mu(s)\geq 0, \sum_s\mu(s)=1$加权，这样我们就得到了目标函数(描述估计器与真值的error)均方误差(Mean Square Value Error, MSE)， $\overline{\mathrm{VE}}$：

$\overline{\mathrm{VE}}(\mathbf{w}) \doteq \sum_{s \in \mathcal{S}} \mu(s)\left[v_{\pi}(s)-\hat{v}(s, \mathbf{w})\right]^{2}$

其中 $\mu(s)$往往选择为在s所消耗的时间(离散的话就是steps的数量)，叫做on-policy分布，在continuing任务中是一个确定的平稳分布，我们在讲MDP时已经介绍过，而对于episodic任务，则比较复杂：

The on-policy distribution in episodic tasks
对于episodic任务，其on-policy分布有所区别。用 $h(s)$表示一个episode从s开始的概率，用 $\eta(s)$表示在平均在单个episode内s消耗的steps的数量，用 $\bar{s}$表示前序状态，则得到 $\eta(s)$的表达式(请仔细思考具体含义)：
$\eta(s)=h(s)+\sum_{\overline{s}} \eta(\overline{s}) \sum_{a} \pi(a | \overline{s}) p(s | \overline{s}, a),$ for all $s \in \mathcal{S}$
这个方程组可以直接求解。归一化：
$\mu(s)=\frac{\eta(s)}{\sum_{s^{\prime}} \eta\left(s^{\prime}\right)}, \quad$ for all $s \in \mathcal{S}$
如果有折扣因子 $\gamma$，则需要添加到 $\eta(s)$的表达式中的第二项上。

但是 $\overline{\mathrm{VE}}$是最好的性能指标吗？我们的目的是学习值函数从而得到更好的策略，但是最小化 $\overline{\mathrm{VE}}$与这个目标是不完全一致的，但是目前还没有更好的替代方案。

一个理想的目标是找到全局最优的 $\textbf{w}^*$，也就是找到 $\textbf{w}^*$使之满足 $\overline{\mathrm{VE}}\left(\mathbf{w}^{*}\right) \leq \overline{\mathrm{VE}}(\mathbf{w})$，这对于简单的线性函数拟合器是可能的，对于复杂的则几乎不可能，我们只能以局部最优替代，对于非线性函数拟合器这是我们能做到的最好的了，也足够了。实际上，目前我们无法保证收敛到最优甚至是最优附近的一个界内，有些方法甚至是发散的。

后面两个小节我们讨论如何把RL的值预测方法和函数拟合方法结合，使用RL值预测方法的updates作为拟合器的训练样本，然后分析哪种方法的 $\overline{\mathrm{VE}}$能更小，函数值拟合方法范围很大(很多)，但是关于他们能否可靠估计我们却知之甚少，因此我们只考虑部分可行方法：基于梯度原则的方法，即线性梯度下降法，它们覆盖了拟合方法的核心问题。

4.随机梯度和半梯度方法

这里介绍一大类方法：随机梯度下降SGD，在函数拟合中用得很广泛也很适合online RL。

在SGD中， $\textbf{w}$是一个列向量 $\textbf{w}\doteq (w_1,...,w_d)^T$，每个元素都是实数。而值函数 $\hat{v}(s, \textbf{w})$是 $\textbf{w}$的微分方程，我们在每个离散的时间步更新 $\textbf{w}$，因此记为 $\textbf{w}_t$。

在每个时间步，我们能得到一个 $S_t$，通过拟合函数可以计算出 $\hat{v}(S_t, \textbf{w}_t)$，此外，假设我们还能得到一个目标值 $v_\pi(S_t)$，它是值函数在状态 $S_t$时的较准确值(目标值)。注意函数拟合器的能力是有限的，不可能完美拟合所有样本的值 $S_t\rightarrow v_\pi(S_t)$。

假设所有样本具有同样的权重，则SGD沿着 $\overline{\mathrm{VE}}$的负梯度方向走一小步，从而减小 $\overline{\mathrm{VE}}$：

$\begin{aligned} \mathbf{w}_{t+1} & \doteq \mathbf{w}_{t}-\frac{1}{2} \alpha \nabla\left[v_{\pi}\left(S_{t}\right)-\hat{v}\left(S_{t}, \mathbf{w}_{t}\right)\right]^{2} \\ &=\mathbf{w}_{t}+\alpha\left[v_{\pi}\left(S_{t}\right)-\hat{v}\left(S_{t}, \mathbf{w}_{t}\right)\right] \nabla \hat{v}\left(S_{t}, \mathbf{w}_{t}\right) \end{aligned}$

其中梯度项为：
$\nabla f(\mathbf{w}) \doteq\left(\frac{\partial f(\mathbf{w})}{\partial w_{1}}, \frac{\partial f(\mathbf{w})}{\partial w_{2}}, \ldots, \frac{\partial f(\mathbf{w})}{\partial w_{d}}\right)^{\top}$

SGD是一种梯度下降方法，每个step的更新量与梯度成正比，因为我们只利用了一个样本/一些样本计算梯度，因此是stochastic的。

因为拟合器的容量是有限的，我们不必让误差收敛到0，且如此可以保证拟合器具有一定的泛化能力。当参数 $\alpha$随着拟合逐渐收敛到0时(满足第二章讲的收敛条件)，则SGD能保证全局的收敛性。

由于我们无法直接得到 $v_\pi(S_t)$，我们只能得到一个估计值(替代值)，然后我们保证这个替代值能逐渐收敛到真实值就行，我们记这个估计值为 $U_t$。因此我们把拟合函数的估计公式替换如下，如果 $U_t$是无偏估计，那么只要更新步长 $\alpha$满足收敛序列条件， $\textbf{w}_t$就能收敛到局部最优：

$\mathbf{w}_{t+1} \doteq \mathbf{w}_{t}+\alpha\left[U_{t}-\hat{v}\left(S_{t}, \mathbf{w}_{t}\right)\right] \nabla \hat{v}\left(S_{t}, \mathbf{w}_{t}\right)$

下面给出了MC状态值预测的梯度下降版本。这与MC方法把在多个episodes中出现的多次s的 $G_t(s)$取平均不同，这里只考虑单个episode中的 $G_t$作为更新目标，这个更新目标是无偏的，因此能保证得到一个局部最优解：

而用boostrapping方法作为 $U_t$是无法保证SGD收敛到局部最优的。因为无论是n-step returns还是DP式的目标，都是依赖于参数 $\textbf{w}_t$的，这导致目标是有偏的，或者说求导时， $U_t$和 $\hat{v}(S_t, \textbf{w}_t)$都与 $\textbf{w}_t$有关，因此不能只对 $\hat{v}(S_t, \textbf{w}_t)$求导，而强行用SGD公式的话，则相当于忽略了 $\textbf{w}_t$对target的影响，这叫做半梯度(semi-gradient)方法。

但是考虑学习的快速性和online/continual特性，semi-gradient方法还是很常用的，实践证明其效果不错。这里给出了semi-gradient TD(0)方法的伪代码：

state-aggregation是一种特殊的梯度方法，其函数估计器类似于查表，但是多个states公用一个估计值，所有states构成多个group，因此每次只更新存在 $S_t$的那个group的值，而参数就是值本身，因此该group的导数是1，其它都是0。下面给出例子具体说明这种特殊的方法：

example 9.1 State Aggregation on the 1000-state Random Walk

这里给出了1000个状态的随机游走问题，特殊之处在于，处于状态s时，等概率选择左右各100个状态中的一个作为transition，如果某一侧没有100个状态，则把这些缺失的状态的转移概率都归入该侧的terminal state中去。将1-100作为一组，101-200作为一组…，共10组，利用state-aggregation MC更新，可以得到阶梯状的曲线。

但是state-aggregation方法会受到状态出现概率的影响。图中下方的灰色部分是各个状态出现的概率曲线，最左侧的group(台阶)偏向于右边界(概率大的)，自右侧的group偏向于左边界。这可能也算是比较合理的，因为毕竟在每个group中要考虑各个状态出现概率的影响。

5.线性方法

函数拟合器最重要的一个实例就是线性模型，将状态特征的每个分量 $x_i(s)$与一个实数 $w_i$相乘，可以写成向量形式：

$\hat{v}(s, \mathbf{w}) \doteq \mathbf{w}^{\top} \mathbf{x}(s) \doteq \sum_{i=1}^{d} w_{i} x_{i}(s)$

这种情况下，我们说值函数是线性的。

$x(s)$是状态s的特征，我们把特征函数叫做basis functions，我们会在下一个小节介绍一些特征表示方法。

线性函数拟合器关于参数 $\textbf{w}$的导数就是状态特征本身 $x(s)$，因此这个update是比较好实现的，因而几乎所有收敛性的讨论都是在线性函数拟合器上讨论的。

在线性拟合器中，只有一个最优值(针对特征而言)，因此局部最优就是全局最优。例如，对于梯度MC算法，如果 $\alpha$满足收敛性条件，那么 $\overline{\mathrm{VE}}$就能收敛到全局最优。

semi-gradient TD(0)在线性拟合器上也能收敛接近全局最优的一个点，我们深入讨论下。记 $x_t=x(S_t)$，首先改写下 $\textbf{w}$的更新公式：

$\begin{aligned} \mathbf{w}_{t+1} & \doteq \mathbf{w}_{t}+\alpha\left(R_{t+1}+\gamma \mathbf{w}_{t}^{\top} \mathbf{x}_{t+1}-\mathbf{w}_{t}^{\top} \mathbf{x}_{t}\right) \mathbf{x}_{t} \\ &=\mathbf{w}_{t}+\alpha\left(R_{t+1} \mathbf{x}_{t}-\mathbf{x}_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right)^{\top} \mathbf{w}_{t}\right) \end{aligned}$

对上式求期望，有：

$\mathbb{E}\left[\mathbf{w}_{t+1} | \mathbf{w}_{t}\right]=\mathbf{w}_{t}+\alpha\left(\mathbf{b}-\mathbf{A} \mathbf{w}_{t}\right)$
其中，
$\mathbf{b} \doteq \mathbb{E}\left[R_{t+1} \mathbf{x}_{t}\right] \in \mathbb{R}^{d} \quad$ and $\quad \mathbf{A} \doteq \mathbb{E}\left[\mathbf{x}_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right)^{\top}\right] \in \mathbb{R}^{d} \times \mathbb{R}^{d}$

如果系统是收敛的，记收敛时的参数为 $\mathbf w_{TD}$，那么有：

$\begin{aligned} \mathbf{b}-\mathbf{A} \mathbf{w}_{\mathrm{TD}} &=\mathbf{0} \\ \Rightarrow & \mathbf{b}=\mathbf{A} \mathbf{w}_{\mathrm{TD}} \\ \Rightarrow & \mathbf{w}_{\mathrm{TD}} \doteq \mathbf{A}^{-1} \mathbf{b} \end{aligned}$

我们称上式叫做TD固定点(TD fixed point)，它稍微偏离了全局最优点。而实际上，线性半梯度TD(0)可以收敛到固定点上。下面给出证明。

Proof of Convergence of Linear TD(0)
首先改写 $\mathbb{E}\left[\mathbf{w}_{t+1} | \mathbf{w}_{t}\right]=\mathbf{w}_{t}+\alpha\left(\mathbf{b}-\mathbf{A} \mathbf{w}_{t}\right)$为： $\mathbb{E}\left[\mathbf{w}_{t+1} | \mathbf{w}_{t}\right]=(\mathbf{I}-\alpha \mathbf{A}) \mathbf{w}_{t}+\alpha \mathbf{b}$
可以看到参数的收敛性只与 $\mathbf A$有关。为了建立直觉，首先考虑 $\mathbf A$是对角矩阵，这有几种情况：
1.如果 $\mathbf A$有负的元素，那么 $\mathbf I-\alpha \mathbf A$的对应元素就是大于1的，对应的 $\mathbf w_t$元素将发散；
2.如果 $\mathbf A$的元素都是正的，那么调整 $\alpha$可以保证将 $\alpha \mathbf A$的元素压缩到 $(0, 1)$的范围，从而 $\mathbf I-\alpha \mathbf A$的所有元素也是在 $(0, 1)$范围的，保证了收敛性。
如果 $\mathbf A$不是对角的，那么只要 $\mathbf A$是正定的( $y^T\mathbf Ay>0$)就能保证 $\mathbf w_t$收敛到0。我们把 $\mathbf A$展开，得到：
$\begin{aligned} \mathbf{A} &=\sum_{s} \mu(s) \sum_{a} \pi(a | s) \sum_{r, s^{\prime}} p\left(r, s^{\prime} | s, a\right) \mathbf{x}(s)\left(\mathbf{x}(s)-\gamma \mathbf{x}\left(s^{\prime}\right)\right)^{\top} \\ &=\sum_{s} \mu(s) \sum_{s^{\prime}} p\left(s^{\prime} | s\right) \mathbf{x}(s)\left(\mathbf{x}(s)-\gamma \mathbf{x}\left(s^{\prime}\right)\right)^{\top} \\ &=\sum_{s} \mu(s) \mathbf{x}(s)\left(\mathbf{x}(s)-\gamma \sum_{s^{\prime}} p\left(s^{\prime} | s\right) \mathbf{x}\left(s^{\prime}\right)\right)^{\top} \\ &=\mathbf{X}^{\top} \mathbf{D}(\mathbf{I}-\gamma \mathbf{P}) \mathbf{X} \end{aligned}$
其中 $\gamma$小于1， $\mu(s)$是Markov Chain稳定分布(stationary distribution)， $\mathbf P$是 $|\mathbf S| \times|\mathbf S|$的概率矩阵， $\mathbf D$是以 $\mu(s)$为对角元素的 $|\mathbf S| \times|\mathbf S|$的对角阵， $\mathbf X$是 $|\mathbf X|\times d$的，每行是一个 $\mathbf x(s)$。式子中， $\mathbf D(\mathbf I-\gamma \mathbf P)$决定了 $\mathbf A$是否正定。下面证明正定性：
首先我们知道，任何实对称矩阵 $\mathbf S$如果对角元素是正的，且比对应的行/列的其他元素的绝对值的和大，那么 $\mathbf S$是正定的。而 $\mathbf D(\mathbf I-\gamma \mathbf P)$显然所有对角线元素都是正的，而所有非对角线元素都是负的，满足了第一个条件；P的每一行之和是1，而乘 $\gamma$之后就不到1了，那么 $1-\gamma \sum\limits_jP_{ij}>0$，因此满足每一行非对角元素的绝对值之和小于对角元素；接下来讨论列，用 $1$表示全1的列向量，则 $\mathbf 1^T\mathbf D(\mathbf I-\gamma \mathbf P)$表示矩阵列和构成的行向量，且由于Mackov Chain平稳分布的性质，有 $\mu =\mathbf P^T\mu$，可证明各列之和也是大于0的：
$\begin{aligned} \mathbf{1}^{\top} \mathbf{D}(\mathbf{I}-\gamma \mathbf{P}) &=\boldsymbol{\mu}^{\top}(\mathbf{I}-\gamma \mathbf{P}) \\ &=\boldsymbol{\mu}^{\top}-\gamma \boldsymbol{\mu}^{\top} \mathbf{P} \\ &=\boldsymbol{\mu}^{\top}-\gamma \boldsymbol{\mu}^{\top} \\ &=(1-\gamma) \boldsymbol{\mu}^{\top} \end{aligned}$
因此on-policy TD(0)是稳定的。

在TD不动点，还可以得到其 $\overline{\mathrm{VE}}(\mathbf w_{TD})$与梯度下降MC方法 $min_\mathbf w\overline{\mathrm{VE}}(\mathbf w)$的不等关系：

$\overline{\mathrm{VE}}\left(\mathbf{w}_{\mathrm{TD}}\right) \leq \frac{1}{1-\gamma} \min _{\mathbf{w}} \overline{\mathrm{VE}}(\mathbf{w})$

因为 $\gamma$接近1，所以这个上界也是挺大的，但是TD方法方差比MC却小很多，因此哪个更好还需要权衡。对于其它on-policy bootstrapping方法，也可以得到类似的上界。例如线性半梯度DP，半梯度Sarsa(0)；对于episodic任务，也能得到类似的结果。

但是注意一定要按照on-policy分布更新，其它更新分布可能导致迭代发散，这个在11章中讨论。

example 9.2 Bootstrapping on the 1000-state Random Walk

state aggregation是线性函数拟合器的特殊形式，我们还讨论random walk这个问题。左图显示了利用semi-gradient TD(0)方法的效果，可见与MC相比效果变差了不少。为了提高效果，我们考虑n-step方法，右图给出了不同n时n-step semi-gradient TD方法的前10个episode平均RMS误差随着参数 $\alpha$的变化过程，注意这里用的是RMS误差而不是 $\overline{\mathrm{VE}}$。

半监督n-step TD算法是表格n-step TD算法的自然扩展，伪代码如下：

其中，更新公式具体为：
$\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1}+\alpha\left[G_{t : t+n}-\hat{v}\left(S_{t}, \mathbf{w}_{t+n-1}\right)\right] \nabla \hat{v}\left(S_{t}, \mathbf{w}_{t+n-1}\right), \quad 0 \leq t<T$

update target 的计算公式具体为：
$G_{t : t+n} \doteq R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1} R_{t+n}+\gamma^{n} \hat{v}\left(S_{t+n}, \mathbf{w}_{t+n-1}\right), \quad 0 \leq t \leq T-n$

6.线性方法的特征构建

线性方法的优势在于对收敛性的保证，而且实践中在数据利用率与计算上都非常高效，而这也需要选择恰当的特征。在强化学习中，针对任务合理选择特征，是一种引入先验领域知识的重要途经。直觉上，特征应该能保证较好的泛化性，例如：对于几何物体，以其可能的形状、颜色、大小等作为特征比较合适；对于移动机器人，以位置、剩余电量程度、声纳传感器数据等作为特征比较合适。

用线性形式也有一些局限性，例如无法考虑特征之间的关联。例如，在倒立摆问题中，较高的角速度是否好跟当前角度是相关的，当偏离较小时，较低的角速度具有更好的修正效果；而偏离较大时，较高的角速度修正效果更好。因此，我们必须考虑不同状态维度之间关联性，下面介绍一些典型方法。

6.1.多项式特征

很多问题的状态都是数值型的，例如倒立摆(pole-balancing)中的位置和速度、Jack’s car rental问题中每个停车场车子的数量等。在这类问题中，RL方法的函数拟合器与插值/回归问题非常相似，很多在插值/回归问题中使用的特征也能在RL中使用，而多项式方法是其中最简单的，但是效果与后面介绍的其它方法相比就差了些。

作为例子，假设RL问题的状态是二维的，且每个维度都是数值型的。对于某个特定的状态s，我们用 $s_{1} \in \mathbb{R}$和 $s_{2} \in \mathbb{R}$表示其两个维度的数值。我们可以简单地选择状态本身作为特征： $\mathbf{x}(s)=(s_1, s_2)^\top$，但这没考虑它们之间的关联，且如果 $s_1, s_2$都是0的话，那么线性拟合器的值始终是0。这两个问题都能通过如下形式的特征改善： $\mathbf{x}(s)=\left(1, s_{1}, s_{2}, s_{1} s_{2}\right)^{\top}$。当然，我们也可以选择更高维的特征： $\mathbf{x}(s)=\left(1, s_{1}, s_{2}, s_{1} s_{2}, s_{1}^{2}, s_{2}^{2}, s_{1} s_{2}^{2}, s_{1}^{2} s_{2}, s_{1}^{2} s_{2}^{2}\right)^{\top}$，从而达到更好的效果。这样处理后，虽然我们的拟合器还是线性的，却成为了状态的二次乃至高次函数。我们可以给出这种方法的一般形式：

假设状态有k个维度： $s_1, s_2, ..., s_k$，且 $s_{i} \in \mathbb{R}$。对于这个k维状态空间，每个n阶多项式特征 $x_i$可以写成：
$x_{i}(s)=\Pi_{j=1}^{k} s_{j}^{c_{i, j}}$
其中， $c_{i, j}$是集合 ${0, 1, ..., n}$中的元素，不重复地，共有 $(n+1)^k$个特征。

高阶多项式特征可以实现更复杂、精确的拟合器，但是由于n阶特征数量会随着状态维度k指数增长，我们往往根据先验信息选择特征空间中的一个子集，也可以利用一些自动选择方法选择子集。

6.2.傅里叶特征

另一种函数拟合方法是基于傅里叶级数的，傅里叶级数可以将周期函数表示为一系列不同频率的sin/cos函数加权求和的形式。傅里叶特征很容易在RL中应用，并且在很多RL问题中都表现得不错。

首先考虑一维的问题。对于周期为 $\tau$的函数，傅里叶级数的频率都是 $1/\tau$的整数倍；对于非周期函数，如果我们只关心该函数的某个有界区间，那么我们可以以该区间的长度作为周期 $\tau$进行延拓。进一步地，如果我们设置 $\tau$为有界区间的两倍，那么我们只需要考虑 $[0, \tau/2]$这个区间，此时可以只用cos函数构造傅里叶级数(因为此时函数延拓后是偶函数)[!原书这里说得很模糊，自行理解就好!]; 对应地，也可以设法只使用sin函数，只需令延拓后的函数是奇函数。通常，我们是构造偶函数的，因为延拓后构造的奇函数在原点处容易不连续。当然，有时同时使用sin/cos特征可能取得更好的效果。

如果令 $\tau=2$，那么特征就定义在区间 $[0, 1]$上，一维n阶傅里叶特征包含n+1个特征：

$x_{i}(s)=\cos (i \pi s), \quad s \in[0,1], \quad for \ i=0,...,n$

下面给出了 $n=1,2,3,4$时的特征图：

对于多维，则按照如下处理：

假设状态有k个维度： $s_1, s_2, ..., s_k$，且 $s_{i} \in [0, 1]$。n阶傅里叶余弦变换的第i个特征为：
$x_{i}(s)=\cos \left(\pi \mathbf{s}^{\top} \mathbf{c}^{i}\right)$
其中， $\mathbf{c}^{i}=\left(c_{1}^{i}, \ldots, c_{k}^{i}\right)^{\top}$， $c_{j}^{i} \in\{0, \dots, n\}$ for $j=1, \dots, k$ and $i=0, \dots,(n+1)^{k}$
共有 $(n+1)^k$种可能的整数向量 $\mathbf{c}^{i}$，内积 $\mathbf{s}^{\top} \mathbf{c}^{i}$则为状态的每个维度分配了一个整数。

举个例子：如果 $k=2$，则 $\mathbf{s}=\left(s_{1}, s_{2}\right)^{\top}$且 $\mathbf{c}=\left(c_{1}, c_{2}\right)^{\top}$，下图是其中的6种特征(横/纵坐标分别是 $x_1, x_2$，颜色是特征数值)：

使用傅里叶特征时，学习算法最好针对不同的特征取不同的更新步长。可以按照原则： $\alpha_i = \alpha / \sqrt{(c^i_1)^2 + ... + (c^i_k)^2}$，当所有 $c^i_j=0$时，取 $\alpha_i=\alpha$。

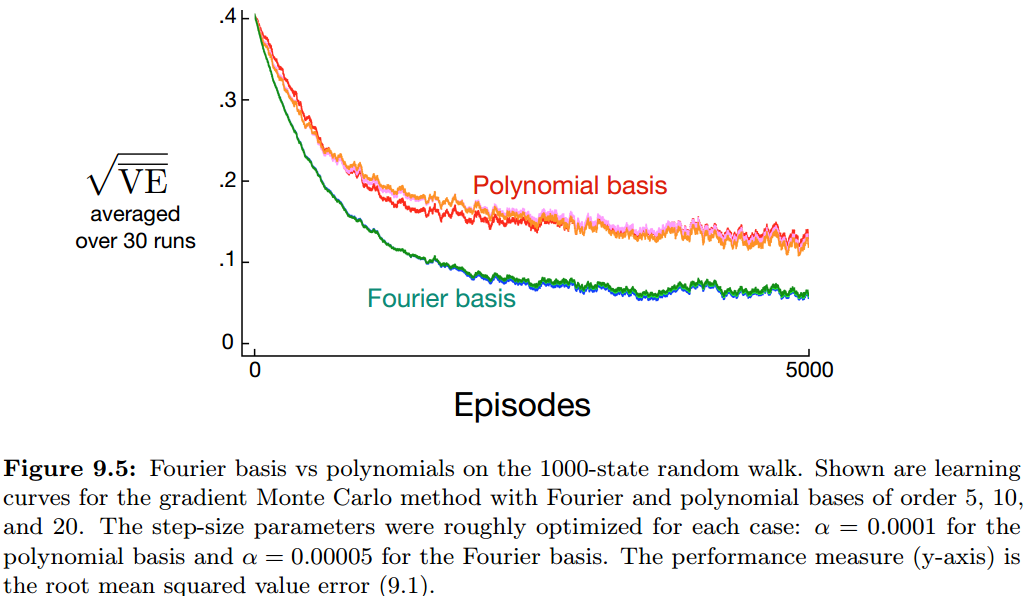
基于傅里叶余弦特征的Sarsa算法比其它类型特征下的算法都要好(多项式，径向基函数)，但是傅里叶特征对于不连续函数则很难处理。

n阶傅里叶特征的数量也是随着状态的维度指数增长的，但是如果k比较小，那么就可以使用所有的傅里叶特征；对于高维状态空间，则必须选择这些特征中一个子集，这可以根据先验或者利用自动化的方法选择。傅里叶特征具有一些优点：可以通过选择合理的 $c^i$引入可能状态维度之间的关联，或者限制 $c^j$向量的值以过滤掉高频噪音。但是傅里叶表征的是全局性质，无法表征局部性质。

下图给出了在1000-states random walk问题中，傅里叶特征的优势：

6.3.粗糙编码特征

如果状态是二维连续数值型的，那么可以在二维平面上画很多交叠的圆，以这些圆作为特征。如果状态在某个圆内，那么对应的特征值就是1，也叫做present；否则，对应的特征值就是0，也叫做absent。这种特征叫做二值特征(binary feature)，它粗略的表征了状态的位置，因此叫做粗糙编码。

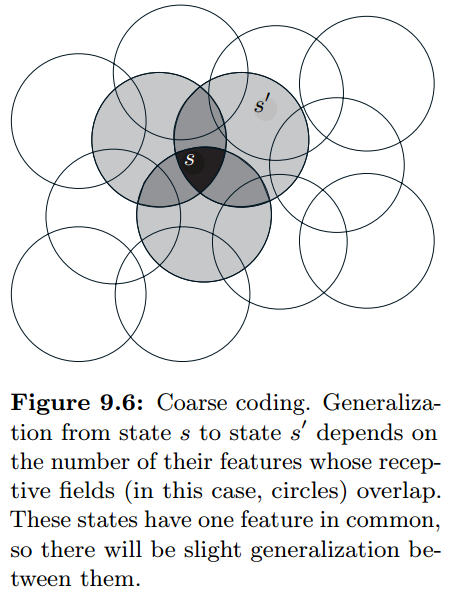
对于线性拟合器来说，每个特征都对应了一个 $\textbf w$的分量，因此对于某个状态，只有那些覆盖了这个状态的圆的权重才能被学习。此外，由于每个圆都覆盖了一定范围，某个状态造成的权重更新，也会泛化到圆内的点上。因此，特征的大小、密度，甚至形状都对泛化有影响。

具有更大感受野(receptive fields)的特征泛化就更广，但是精确度可能下降。通常，初始泛化能力主要受特征的大小和形状影响；敏锐度(最小分辨率)则主要受特征的数量(密度)影响。

example 9.3 Coarseness of Coarse Coding
这个例子主要阐明粗糙编码感受野大小对学习的影响。利用线性拟合器与粗糙编码学习一维方波函数，以函数的值作为学习目标，记为 $\boldsymbol{U}_{t}$。由于问题是一维的，因此粗糙特征是一维的区域(取三种粒度：narrow，medium，broad，密度相同)，而不是二维的圆。而训练samples在函数自变量区间内均匀选择，步长设置为 $\alpha=\frac{0.2}{n}$，其中n是present状态的特征数量。从学习结果中我们可以看到，特征的宽度在学习开始时影响很大，因为只能泛化到覆盖该状态的区间内的点(与特征尺寸密切相关)；而最终的学习结果基本上是差不多的。这说明感受野形状对初始泛化影响很大，但是对渐进解的影响很小。

6.4.瓦片编码特征

瓦片(tile)编码是粗糙编码在多维连续空间中的特殊形式，这种方法更加灵活和高效。这也许是对于现代串行数字计算机最可行的特征表示方法。

在瓦片编码中，特征被分组成多个“分割”，每个“分割”都完整地覆盖状态空间。我们把这种分割叫做瓦片层(tiling)，每个瓦片层上我们再分成多个瓦片，这些瓦片的作用和粗糙编码中的圆是类似的，但是它们是矩形的，且没有交叠，我们往往在每个层中将瓦片均匀分配。如果我们只构建一个层，那么每个点都会被唯一的瓦片覆盖(因为没有交叠)，那么就退化成了聚类算法而不是粗糙编码了。

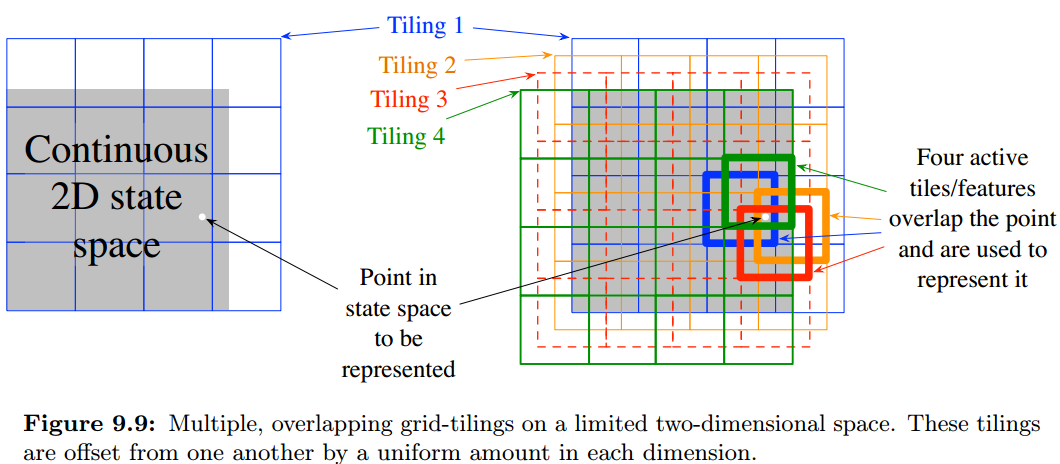
因此，我们必须使用多个tilings，且每个tiling之间进行一定的偏移。如果一个tiling我们划分成 $4*4$的网格，共构造4层，那么特征数量就是 $4*4*4=64$个，对应64个权重分量。对于1000状态的random walk问题，可以明显看到多tiles的优势。

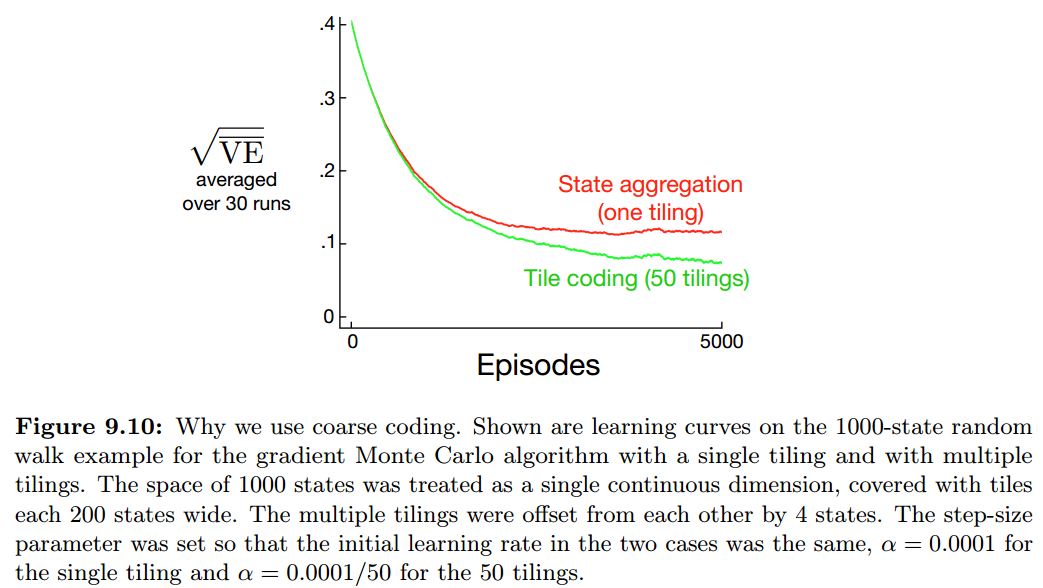
Tile coding的优点在于，present的特征数量是恒定的：每个tiling一个。所以更新步长 $\alpha$可以设置为比较固定的值，例如可以设置为 $\alpha=\frac{1}{n}$，n表示tilings的数量，这样我们可以一步到位地学习到值函数，也就是无论 $\hat{v}\left(s, \mathbf{w}_{t}\right)$是多少，一定有 $\hat{v}\left(s, \mathbf{w}_{t+1}\right)=v$，这个性质叫做one-trail learning。当然，如果数据有噪声/考虑泛化，我们还是希望能逐渐逼近值函数而不是一步到位，因此可以缩小步长，例如设置 $\alpha=\frac{1}{10 n}$。

Tile coding还有计算上的优势，因为特征是0/1二值的，那么我们实际上只需要把n个层上对应的present的特征的权重相加即可，非常简单。而且，通常 $n \ll d$，d是特征的总数量。

Tile coding的泛化能力与tiling的偏移密切相关，如果沿着每个方向均匀地偏移，那么不同的状态可以按照多种方式泛化，下图上半部分给出了八种偏移方式(patterns)，均匀偏移的方式会引入不必要的泛化偏差(引入了不对称倾向)，而随机偏移则更加合理，图中下半部分给出了随机偏移的效果，它们相对于被训练的点都不会表现出明显的不对称性。

图中给出的是单个瓦片的示意，而不是多个层的示意。

每个tilings之间的offset不能超过一个tile的宽度。如果用 $w$表示tile的宽度，n表示tilings的数量，那么 $\frac{w}{n}$，就是基本偏移单位。这样对于一个tile，总有一个边长为 $\frac{w}{n}$正方形和其它所有的tiling的对应区域重叠。均匀偏移按照这个基本单位沿着各个方向依次偏移；可以用向量 $(1,1)$表示沿着两个维度都偏移一个单位。

不同的偏移向量具有不同的效果，合理设置就可以避免非对称性。目前推荐使用如下这样的偏移向量：对于k维状态空间，可以选择 $(1,3,5,7, \ldots, 2 k-1)$这样的向量，且令n(tiling的数量)满足 $n=2^{t} \geq 4 k$，t我们选择满足不等式的最小的。上图中下侧的偏移就是根据这种方法构造的，其偏移向量为 $(1,3)$，因此依次(超过width就减去width，约束到一个width以内)偏移 $(1,3), (2, 6), (3, 9-8=1), (4, 12-8=4), (5, 15-8=7), (6, 18-16=2), (7, 21-16=5)$。目前的开源软件已经能高效地为k维向量生成tilings。

至于构造tile coding的策略，我们可以设定tilings的数量以及tiles的形状，达到随机偏移的目的。tilings的数量和tiles的尺寸决定了最后渐进的精度，而tiles的形状则决定了泛化的特性，下面是一些典型的形状，左侧随机形状(不常用)，中间的注重竖轴维度的泛化，且当数值小的时候分辨率更高，右侧则更重视对角方向的泛化。

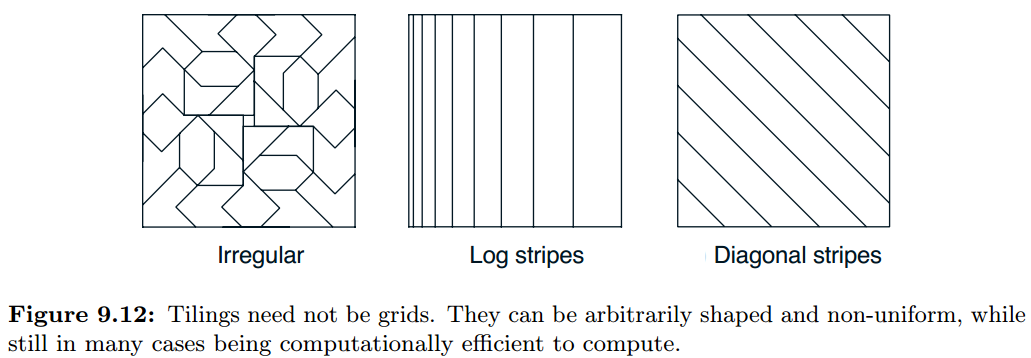
实践中，我们常在不同的层中使用不同的tiles形状。我们可以在不同的层重视不同方向的泛化(各种条状)，在某些层考虑维度之间的联合作用(矩形碎块)，这样我们就能组合出泛化能力强大的特征。然而，目前自动化地构建tilings的方法还不够成熟，我们还是需要手动设计。

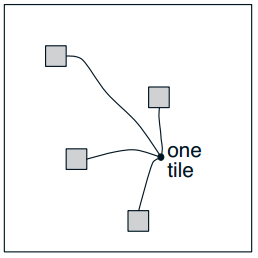
为了降低内存消耗，我们可以使用hashing方法。也就是，首先我们把状态空间分成比较碎的块，然后使用hash算法把碎块分配到粒度更大的几个集合中，每个集合包括整个状态空间中不相邻的一些碎块，如下图所示，就表示了一个hashing集合。注意这也是能覆盖所有状态空间的。之所以能这么做，是因为只有状态空间中的一部分才需要高的分辨率[不知如何理解？]，其它部分可能不需要。hashing方法缓解了维度诅咒的问题，同时还不需要针对具体任务特殊处理。开源实现中往往包含了hashing方法。

6.5.径向基特征

径向基函数RBFs也很常用[很多文献都有涉及，课题组之前整理文献过程中看到了很多]。这是粗糙编码向连续值特征的自然扩展，也就是特征的值不再是0/1二值的，而是在[0, 1]区间的，反映了该特征的强度。一个典型的RBF特征是以状态 $s$和特征中心 $c_i$之距离作为参数的高斯函数，并由参数 $\sigma_i$控制宽度。

$x_{i}(s) \doteq \exp \left(-\frac{\left\|s-c_{i}\right\|^{2}}{2 \sigma_{i}^{2}}\right)$

所谓的距离如何定义，则可以根据具体任务确定，可以是各种范数等等。基于二范数的一维RBF特征如图所示。

RBFs的优势：产生的拟合器更加平滑，且处处可微，但是在实际中这没有太大的优势。RBFs还需要更多的计算，当维度超过二时往往会降低性能，因为在高维问题中，tiles的边界实际上是更重要的。

以RBFs作为节点，可以构造线性函数估计器 —— RBF网络。RBF网络也是利用梯度下降法学习的。此外，一些学习方法还能改变RBFs的中心与宽度参数，这样就可以进行非线性函数估计了。非线性方法实际上往往是效果更好的，其缺点也是明显的：计算量更大，且需要很多人工参数设定。

7.手动选择步长参数

大多数SGD方法都需要设计者选择合适的步长参数 $\alpha$，能自动选择是最好的，但实际中往往还是得手工设置。因此，我们需要首先建立对参数 $\alpha$的直观认识，找到设置参数 $\alpha$的比较通用的方法。

理论上的分析在实际中往往没什么作用，实际上我们在第二章就给出了 $\alpha$序列的收敛条件，为了满足该条件我们就不得不缓慢降低步长大小，这通常会导致学习速度过慢。实际中，我们常设置 $\alpha_{t}=1 / t$，在表格MC方法中这相当于求样本均值，而在使用TD方法、问题非平稳、或者使用拟合器的场景下就不好用了。

为了更直观地认识更新步长参数的手动调整问题，我们可以回顾下表格类算法的情形。对于表格算法，如果设置更新步长 $\alpha=1$，那么可以一次更新到位，但是考虑到我们往往是bootstrapping地更新，且问题本身、传感器往往具有不确定性，因此我们应该降低步长，逐渐靠近真值。一般地，如果希望 $\tau$次更新后能达到真值，那么设置 $\alpha=\frac{1}{\tau}$即可，这样表格化的估值会靠近targets的均值，且最近的targets的权重更大。

对于函数拟合器方法，就没有上面那么清晰的结论了，因为每个状态之间除了通过bootstrapping相互影响，还通过拟合函数相互影响。我们目前有一个经验性的原则，对于各种线性函数拟合器基本都是适用的：假设希望通过对相同的特征向量进行 $\tau$次更新即基本收敛，线性SGD方法的步长参数应该按照下式设置：

$\alpha \doteq\left(\tau \mathbb{E}\left[\mathbf{x}^{\top} \mathbf{x}\right]\right)^{-1}$

其中， $\mathbf{x}$是根据特征向量分布采样的特征向量样本。当特征向量的模长比较稳定时(不同特征向量的模长很相似，也就是 $\mathbf{x}^{\top} \mathbf{x}$比较固定时)，该方法效果较好[书中没有给出本方法的原理讨论]。

8.非线性函数拟合器：人工神经网络

人工神经网络ANN广泛地用于非线性函数拟合。ANN是由很多具有神经元性质的单元互相连接构成的网络。ANN已经有很长的历史了，深层神经网络，也就是深度学习，近年来展现出了很强的能力，在ML，包括RL领域都涌现了基于深度学习的很多优秀的算法。

如果神经网络的拓扑中没有环，就是一般的前馈ANN；如果有环，就是循环ANN，他们都有很多用途，这里主要探讨前馈ANN。前馈ANN由输入层，隐藏层，输出层构成，不同层的节点之间的连线起到类似神经元中突触的作用，每个连接对应一个实数权值，每个节点对应一个实数偏移，如下图所示：

每个单元(结点)都是半线性的，先把所有输入加权求和，然后在经过一个非线性函数(激活函数)，得到结点的输出。激活函数常采用S型函数(sigmoid)，例如logistic函数 $f(x)=1 /\left(1+e^{-x}\right)$；也有常采用线性整流单元ReLU，即： $f(x)=\max (0, x)$；还可以采用阶梯函数，例如： $f(x)=1$ if $x \geq \theta$ else $f(x)=0$。

拟合函数由网络连接的权重决定，一个没有隐层的ANN表达能力非常有限，但是只要有一个足够宽的以sigmoid型函数激活的隐层，就能拟合任何连续函数(Cybenko，1989)。其它激活函数也是可以的，但是至少是非线性的，并满足一定的条件。

虽然有一个隐层就能近似所有函数，但是经验和理论表明，拟合复杂函数的时候，加深网络往往能取得更好的效果(增加ANN隐层数量)(Bengio, 2009)。多层ANN中，随着层的堆叠，能快速增加抽象表示能力，产生分层逐步抽象的效果。

训练ANN的隐层因此是一种自动提取特征的过程，可以生成层次化的特征，越后面的层越抽象，从而避免手动设计特征，这也是这些年ANN受到如此重视的原因。ANN通常利用SGD学习，这需要我们构造好目标函数，然后最大化/最小化它。监督学习中，常采用网络输出与标签的MSE或者交叉熵。RL中，则可以使用TD误差作为目标；或者最大化期望回报；或者使用策略梯度。为了更新网络的参数，我们必须求目标函数关于各个参数的偏导数，然后就能得到梯度向量了，从而利用梯度下降法更新参数。

如果激活函数是可微的，可以采用反向传播算法计算关于各层参数的梯度，即BP算法(LeCun, 1985; Rumelhart, Hinton, and Williams,1986)。BP算法首先前向计算每层各结点的输出，然后反向计算各个权重的偏导数(真实导数的估计值)。在15章，我们会讨论非BP的训练方法。

反向传播算法的原理见下图[1]：

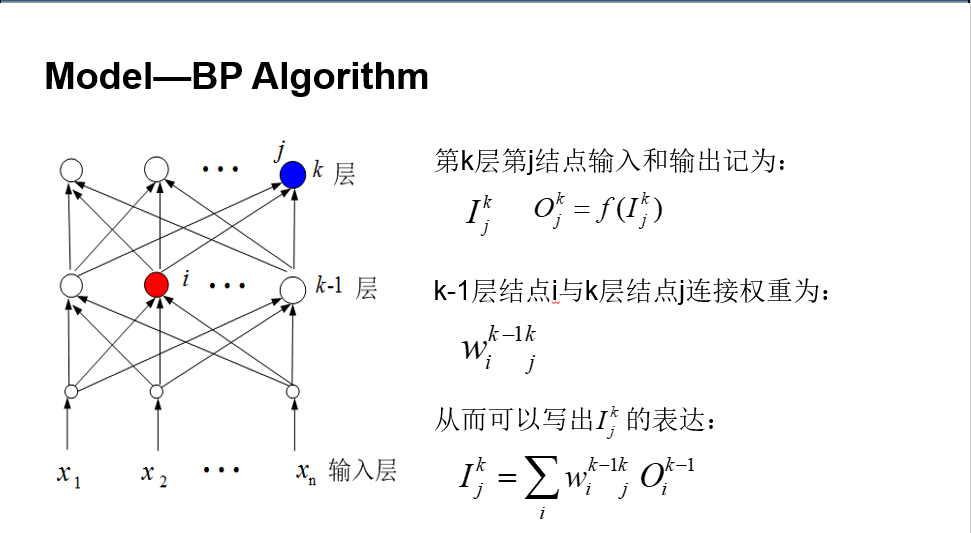
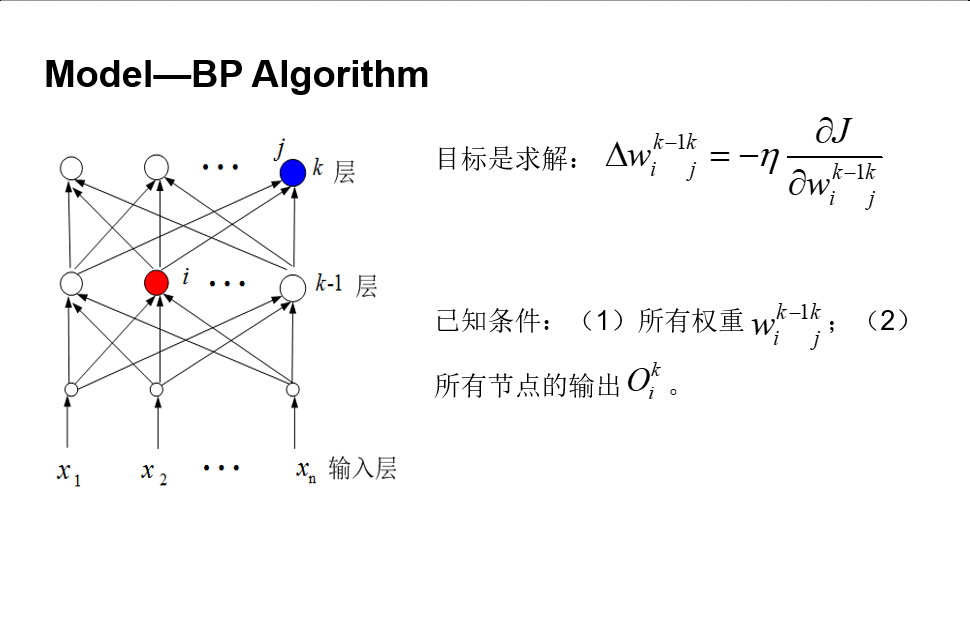
反向传播算法对于浅层神经网络的训练是非常有效的，但是对深层ANN效果就不够好了，甚至加深网络层数反而会导致效果降低，这是因为：1. 更多的权重数量使得容易出现过拟合；2. 层数过多导致梯度消失/梯度爆炸问题。现在很多先进的神经网络结构已经能很好地解决这两个问题了。

过拟合问题是在任何训练数据比较有限，拟合器结构较复杂的时候都会出现。对于online RL，过拟合就不是什么问题，因为训练输入在实时生成，非常多，但是高效的泛化能力却是需要考虑的。对于ANN而言，过拟合是很常见的问题，主要因为ANN参数非常多，但是现在已经有很多方法来抑制过拟合了：提前终止(当在验证集上性能开始下降时就停止训练)、正则化、权重共享(卷积网络等)、dropout方法(随机地去掉一些结点，也就是随机地使一些结点的输出为0，然后在使用的时候把这些结点乘上训练时保留的概率，效果很好)(Srivastava, Hinton, Krizhevsky, Sutskever, and Salakhutdinov，2014)。

梯度消失/梯度爆炸问题是RL中更应该关注的。

深度置信网络DBN是解决深层网络训练的有效方法(Hinton, Osindero, and Teh，2006)。该方法中，各层首先使用非监督学习逐层训练，而不依赖全局目标函数，这个过程可以先提取出输入数据中的统计特征。训练时，首先训练较深的某一层，然后使用这个层的输出作为下层的输入，以训练下一个层，直到所有的权重训练完毕，以这些数值作为监督学习的初始数值，然后通过BP算法结合全局目标微调参数，研究表明这种方法总体上比只使用BP算法好得多[1]。

批标准化(batch normalization, BN)(Ioffe and Szegedy, 2015)也是用来训练深度网络的技术，如果对网络的输入进行标准化，那么学习会容易得多。所谓标准化，一般是调整到0均值，1方差，BN实际上是把每层的mini-batch输出进行标准化后再输入下一层。如下图所示[2]：

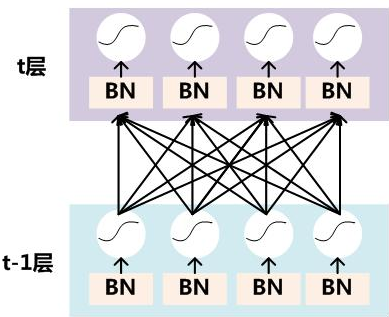
深度残差网络(deep residual learning, He, Zhang, Ren, and Sun, 2016)也可以用来训练深层的网络。有时候，学习函数与输入的差可能是更容易的，也可以降低梯度消失问题，因此残差网络实际上就是在ANN中加入一些shortcut/skip，使层的输入直接连接到层的输出，注意这是不需要增加额外的权重的。目前，BN和残差层在Alpha Go中都使用了。

深度卷积神经网络(LeCun, Bottou, Bengio and Haffner, 1998)是深度学习中非常成功的网络结构，用来处理高维输入数据，例如图像。由于它种特殊的结构，可以不用深度置信等技巧，直接BP训练，结合dropout、residual module、BN等就能达到很好的效果。LeCun在1998年设计的用于手写数字识别MNIST数据集的网络结构如下：

它由相互交替的卷积层和下采样层堆叠，最后加上几个全连接层。每个卷积层都产生几个特征图，所谓特征图指的是某种特征的卷积核扫过全图得到的，全图中与卷积核特征相似的区域就会在下一层对应区域得到较大的值；下采样则指的是池化操作。以上内容具体参考[1]。卷积的主要优势体现在权值共享，可以极大降低参数数量，也相当于引入了一定的先验信息；池化则除了降低维度，也减弱了对特征空间位置的依赖。

基于ANN的RL我们在16章介绍一些目前较好的结果。

9.最小平方TD

目前本章我们讨论的所有方法，在每个时间步需要和参数数量成比例的计算量，更多的计算量往往导致更好的效果。本章我们介绍一个针对线性拟合器很好的方法：LSTD，Least-Squares TD，可以提高数据的利用效率，但是也会导致计算量扩大。

我们之前讨论过，线性估计器渐进地收敛到TD不动点： $\mathbf{w}_{\mathrm{TD}}=\mathbf{A}^{-1} \mathbf{b}$，其中 $\mathbf{A} \doteq \mathbb{E}\left[\mathbf{x}_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right)^{\top}\right] \quad$ and $\quad \mathbf{b} \doteq \mathbb{E}\left[R_{t+1} \mathbf{x}_{t}\right]$。

那么我们为什么一定要迭代计算呢，这实际上降低了收敛的速度，我们可以直接估计 $\mathbf A$ and $\mathbf b$，然后直接计算出不动点。LSTD就是这个思路，它的估计式为：

$\widehat{\mathbf{A}}_{t} \doteq \sum_{k=0}^{t-1} \mathbf{x}_{k}\left(\mathbf{x}_{k}-\gamma \mathbf{x}_{k+1}\right)^{\top}+\varepsilon \mathbf{I} \quad$ and $\quad \widehat{\mathbf{b}}_{t} \doteq \sum_{k=0}^{t-1} R_{k+1} \mathbf{x}_{k}$

其中 $\mathbf I$是单位矩阵，然后选取一个小的 $\varepsilon>0$时使得 $\widehat{\mathbf{A}}_{t}$总是可逆，这里实际上应该除t，但是因为TD不动点有个求逆操作，把t就消掉了，因此这里省略了除t，估计的参数为：

$\mathbf{w}_{t} \doteq \widehat{\mathbf{A}}_{t}^{-1} \widehat{\mathbf{b}}_{t}$

这个算法在数据利用层面是非常高效的，但是计算复杂度却比较高，尤其是跟半梯度方法的 $O(d)$复杂度相比。但是我们可以把 $\widehat{\mathbf{A}}_{t}$和 $\widehat{\mathbf{b}}_{t}$的计算式写成增量的形式，但是由于涉及外积运算，因此复杂度还是 $O\left(d^{2}\right)$的，且 $\widehat{\mathbf{A}}_{t}$的存储复杂度也是 $O\left(d^{2}\right)$的。而 $\mathbf{w}_{t}$还用了求逆操作，该操作的复杂度一般是 $O\left(d^{3}\right)$的，我们也可以写成增量的形式，从而实现 $O\left(d^{2}\right)$的复杂度(第一个等号是改写成增量操作的形式)：

$\begin{aligned} \widehat{\mathbf{A}}_{t}^{-1} &=\left(\widehat{\mathbf{A}}_{t-1}+\mathbf{x}_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right)^{\top}\right)^{-1} \\ &=\widehat{\mathbf{A}}_{t-1}^{-1}-\frac{\widehat{\mathbf{A}}_{t-1}^{-1} \mathbf{x}_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right)^{\top} \widehat{\mathbf{A}}_{t-1}^{-1}}{1+\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right)^{\top} \widehat{\mathbf{A}}_{t-1}^{-1} \mathbf{x}_{t}} \end{aligned}$
for $t>0,$ with $\widehat{\mathbf{A}}_{0} \doteq \varepsilon \mathbf{I}$。

上述式子也叫Sherman-Morrison公式，其复杂度是 $O\left(d^{2}\right)$的。整个算法框架如下：

LSTD方法是否适用，要根据问题的维度d、是否需要快速学习等因素决定，毕竟LSTD复杂度比TD高很多。而且，LSTD不需要设置更新步长，这是一个优势；但是LSTD需要设置参数 $\varepsilon$，其必须选择不大不小的合理数值；此外LSTD没有更重视最近数据的考虑，因此无法遗忘历史数据，在RL中这不是好的性质，因此不得不引入额外的遗忘机制。

10.基于记忆的函数拟合器

到目前为止，我们讨论了参数化的拟合方法，该方法依靠学习算法不断调整参数，从而得到值函数。每次update都是一个训练样本，基于这些数据来学习，更新完成后，训练样本就可以丢弃了，当需要使用拟合器的时候，我们利用最后得到的参数，输入状态，即可输出估计的值。

基于记忆的函数拟合方法则十分不同，它只保存训练样本，而不更新任何参数。但需要使用该模型时，则使用存储的部分数据j计算一个估计值，这种方法有时候也叫lazy learning，因为这种方法是在查询时才处理训练样本的。

基于记忆的函数拟合方法是重要的非参数方法之一。不像参数化方法，拟合函数的形式并不局限于可参数化的函数，而是直接由训练样本决定，然后结合一些将它们结合起来的算法进行估计。记忆的样本越多，则估计越准确。

目前有很多种不同的基于记忆的方法，主要是存储训练样本的方式、如何利用样本查询的方式不同。我们这里只讨论局部学习的方法，即只采用附近的样本求出查询结果。这些方法首先找到记忆中与查询值相近(根据状态的距离)的那些状态，然后计算出查询状态的估值，返回后丢弃这个值。

最简单的方法是nearest neighbor方法(NN)，也就是直接找到和查询状态最近的状态，然后返回它的值；更复杂的，可以寻找最近的k个值，然后利用与查询状态的距离加权；局部权重回归也是类似的，但是它利用附近的一些样本拟合出一个面，注意拟合时的目标函数也用距离加权。

非参数，基于记忆的方法相比参数方法，不会受到拟合函数这个先验的影响，因此当数据持续增多时，效果持续改善；强化学习中往往根据trajectory sampling更新，因此基于记忆的方法可以利用附近轨迹上的临近状态进行拟合；全局拟合往往是没必要的，因为状态空间中的很多区域实际上是不会出现的。此外，基于记忆的方法使得智能体的经验对局部状态估计造成比较显著的影响，而参数化方法则影响很小。

避免全局估计也能很好地克服维度诅咒的问题，例如，对于有k个维度的状态，一个表格化的方法需要k的指数级的存储空间；而基于记忆的方法，每个样本的存储消耗是和k成比例的，总的存储空间则和样本数量n成比例。但是基于记忆的方法也存在问题，当样本数量很大时，搜索最近样本的复杂度就会很高，目前已经有一些不错的方法来解决搜索问题，例如使用多计算机或者特殊硬件；使用专门多维数据结构存储数据。k-dimensional(k-d)树就是一种不错的结构，它递归地把k维空间根据二叉树结点划分为多个区域，根据数据的数量和在状态空间的分布，使用k-d树进行最邻近搜索可以快速缩小搜索区域，使得搜索可行。

局部权重回归需要快速进行局部回归的计算方法，而且每次查询都需要进行回归。目前已经发展出一系列用来解决这个问题的方法，包括限制数据库大小（通过遗忘的方式）等。

11.基于核的函数拟合器

基于记忆的方法是需要根据样本状态与查询状态的距离进行加权，用来分配这些权重的函数叫做核函数，或者简称核。更一般地，核函数不需要与距离有关，也可以是其它衡量状态之间相似度的方法。在加权这个问题中，可以定义： $k : \mathcal{S} \times \mathcal{S} \rightarrow \mathbb{R}$，核 $k\left(s, s^{\prime}\right)$就是衡量 $s$对 $s'$影响的权重。

$k\left(s, s^{\prime}\right)$也可以看作从 $s’$到 $s$泛化强度的度量。核函数从数值上表示两个状态之间的相关程度，例如：瓦片编码的泛化能力与各个tiling是均匀偏移还是不对称偏移有关，每种偏移方法可以等效为一个核函数。实际上，正如我们在下面讨论的，线性参数拟合方法的泛化能力都能用核函数描述。

核回归是基于记忆的方法，它基于核函数，计算所有存储的样本的加权均值。如果 ${D}$是所有存储的样本的集合，用 $g\left(s^{\prime}\right)$表示存储的 $s'$的值，则核回归公式为：

$\hat{v}(s, \mathfrak{D})=\sum_{s^{\prime} \in \mathcal{D}} k\left(s, s^{\prime}\right) g\left(s^{\prime}\right)$

而上一节我们介绍的加权平均方法，则是核回归的特例，采用了特定的权重值(靠近的样本权重不为0，其它都为0)。

RBF函数是常用的核。在之前的特征构建中，RBF的中心和宽度可以是固定的，也可以自动调整的。除了那些自动调整中心和宽度的方法外，这是一种线性参数化方法，参数就是RBF核的权重，这可以通过随机梯度、半梯度下降方法学习。拟合器的形式是提前定义好的RBF核的线性组合的形式。基于RBF的核回归则与RBF特征提取有两点不同：1. 核回归是基于记忆的方法；2. 核回归是非参数的，没有要学习的参数。

当然，核回归在实际应用中还有很多需要讨论的问题，这里就不介绍了，但是可以看到，任何带有特征表示的线性参数回归方法，都能重写成核回归的形式，只需设定 $k\left(s, s^{\prime}\right)$是特征向量 $\mathbf{x}(s)=\left(x_{1}(s), x_{2}(s), \ldots, x_{d}(s)\right)^{\top}$的内积即可：

$k\left(s, s^{\prime}\right)=\mathbf{x}(s)^{\top} \mathbf{x}\left(s^{\prime}\right)$

使用这个函数的核回归可以产生与线性参数方法一样的拟合函数，实际上如果特征向量的模长是一样的，那么这个内积表明的就是两个向量之间的相似程度，数值越大表明越相似。

这里省略了数学上的推导，可以在Bishop, 2006找到。除了构建特征和线性参数拟合器，我们还可以直接构建核函数，从而省略提取特征的过程，直接得到其特征的内积，这在支持向量机(SVM)中用得很多。对于很多特征向量集合，上述这种使用核函数的方法复杂度要比带特征向量的使用线性参数的方法相比低很多，这叫做核技巧，在状态维度很高时效果很好。

12.更关注部分更新：Interest和Emphasis

目前本章我们所介绍的算法，都把所有遇到的状态平等对待，但是有时我们可能对某些状态更感兴趣。例如，在折扣episodic问题中，我们可能对前面的状态(靠近starting状态的)更感兴趣，因为期望折扣累积回报在这些状态上相当于first-visit的，可能更准确；或者在动作值函数的学习中，那些值比较小的动作可能就没有greedy的动作重要。因此，如果我们更侧重重要的状态，效果可能会有改善。

我们之所以平等地对待每个遇到的状态，主要是因为我们是根据on-policy分布更新的。这里我们扩展on-policy分布的内涵：我们认为MDP的on-policy是多个的，根据轨迹的初始化不同而变化。然后我们引入一些新的概念：

1. 非负标量度量：使用随机变量 $I_{t}$(叫做interest)度量我们希望在t时刻准确评估这个状态的值的程度。0表示根本不关心这个状态，1表示我们很重视。interest可以通过很多方式去设置，例如可以依赖时刻t的轨迹或者学习到的参数。 $\overline{\mathrm{VE}}$中的参数 $\mu$则根据轨迹上的分布设置，通过interest加权。
2. 非负随机变量：强调度 $M_{t}$(叫做emphasis)，直接乘到update上，表明强调或者不强调t时刻的这个更新，因此更新公式改为:
   $\mathbf{w}_{t+n} \doteq \mathbf{w}_{t+n-1}+\alpha M_{t}\left[G_{t : t+n}-\hat{v}\left(S_{t}, \mathbf{w}_{t+n-1}\right)\right] \nabla \hat{v}\left(S_{t}, \mathbf{w}_{t+n-1}\right), \qquad 0 \leq t<T$
   强调度如下定义：
   $M_{t}=I_{t}+\gamma^{n} M_{t-n}, \qquad 0 \leq t<T$
   对于所有 $t<0$， $M_{t}=0$。对于MC情形， $G_{t : t+n}=G_{t}$，那么所有更新都是在episode结束时进行的，则 $n=T-t$且 $M_{t}=I_{t}$。

example 9.4 Interest and Emphasis
考虑下面四状态的MRP：

以最左侧的状态作为起始状态，每个转移的回报都标在箭头上，直到到达终止状态。我们取参数 $\mathbf{w}=\left(w_{1}, w_{2}\right)^{\top}$。前两个状态的值设置为 $w_1$，后两个则是 $w_2$。假设我们只对最左侧的状态感兴趣，因此设置最左侧的interest为1，其余都是0。
首先考虑采用梯度MC方法，不考虑interest和emphasis，最后的收敛结果是： $\mathbf{w}_{\infty}=(3.5,1.5)$；而使用本节的方法，则结果为 $w_1=4.0$，而 $w_2$不会被更新，显然本节的方法更加灵活。
然后考虑two-step半梯度方法，则也收敛到 $\mathbf{w}_{\infty}=(3.5,1.5)$，但是本节的方法将收敛到 $\mathbf{w}_{\infty}=(4,2)$。这里之所以能保证第三个状态的更新，是由 $M_{t}$的定义决定的[你可以仔细想想]。

13.总结

如果希望RL方法能应用到AI或者工程应用中，则必须具有泛化能力。为了达成这个目的，需要借助监督学习中已有的技巧，并把每个update当作一个训练样例。

最适用的监督学习方法是那些使用参数化函数拟合器的，即策略通过权重向量w参数化。虽然权重向量拥有很多参数，但是通常状态空间是比这些参数大得多的，因此我们必须要定义目标，以计算梯度。常采用 $\overline{\mathrm{V} \mathrm{E}}(\mathbf{w})$作为参数向量w与on-policy分布 $\mu$下的误差。

为了找到好的参数向量，最常用的方法是随机梯度下降SGD及其变体逐渐更新参数向量w。本章我们聚焦于确定的on-policy策略，讨论的是prediction/evaluation问题。比较自然的方法是n-step 半梯度 TD，包括MC方法和半梯度TD(0)。半梯度TD方法不是真正的梯度方法，因为求偏导的时候，由于bootstrapping，更新目标也是与权重向量有关的。但是实际效果还是不错的。

为了效果更好，常将状态转化为一些特征，并把这些特征乘权重相加，构成基于特征的线性拟合器。如何选择特征则要结合具体问题的领域先验知识，可以选择多项式、傅里叶、粗糙编码、瓦片编码、径向基函数等特征。LSTD是数据利用最高效的TD预测方法，但是需要和权重数量平方关系的计算复杂度；非线性方法包括ANN拟合器，近年来由于深度学习的发展展现出了很强的潜力。

线性半梯度n-step TD方法在标准条件下、对于任意的n是收敛的，且能保证 $\overline{\mathrm{V} \mathrm{E}}(\mathbf{w})$误差有界。当n越大，界区间越小，但是学习越慢。因此一定程度的bootstrapping是必须的。

参考文献

[1].(神经网络基础)https://download.csdn.net/download/u013695457/10428446
[2].(BN)https://www.cnblogs.com/guoyaohua/p/8724433.html