强化学习导论第六章瞬时时间差分法

这一次开第六章，Temporal-Difference 方法，简称TD，可以翻译为瞬时差分法。

TD方法在强化学习算法中有很重要的地位，因为它是一个集大成的算法。TD综合了第五章所说的蒙特卡洛算法和第四章所说的DP算法的特点，既可以从真实经验序列学习，无需环境模型，又可以根据已得到的估计值来更新新的估计值（bootstrap）。这是目前我们需要在脑海中构建的关于TD的一个基本特征。

但是虽然TD综合了蒙特卡洛和DP的特点，终归也有区别。区别在哪？区别在于policy evaluation（也叫做prediction）的过程，也就是根据某一个policy $\pi$ 不断更新其对应的value function $v_\pi$ 的过程。熟悉前面内容的读者们肯定知道，policy evaluation之后还有一个policy improvement（也叫做control）过程，在这个过程中，TD、monte carlo、DP则没有太大的区别，都是采取基于generalized policy iteration (GPI) 的一些变体。因此，我们接下来重点关注它们在policy evaluation过程的区别。

6.1 TD Prediction

我们先来比较一下TD prediction过程和蒙特卡洛 prediction过程的区别：

首先上一个公式： $V(S_t)\leftarrow V(S_t) + \alpha [G_t-V(S_t)]$

上式体现了蒙特卡洛算法的value更新规则，我们叫做constant- $\alpha$ 蒙特卡洛算法。这里我们暂且不考虑多个episode之后的平均化操作，仅就一个episode来说，里面出现的每一个 $S_t$ 对应的value，需要根据这个episode彻底结束之后得到的 $G_t$ 来更新，注意这里的重点是“等待episode结束”。

再来看TD的更新规则公式（具体应该是TD(0)算法，TD类算法中的其中一种：

$V(S_t)\leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]$

找不同，发现前面的 $G_t$ 被换成了 $R_{t+1}+\gamma V(S_{t+1})$ ，这就是区别所在。也就是说，TD算法“不等到episode结束”，而是在下一个时间点，就拿刚刚得到的reward信息和之前 $V(S_{t+1})$ 的estimate来更新 $V(S_t)$ 了。敏感的读者在这里好像还会嗅到一丝DP的含义：拿之前的估计值作为基准，估计新的值，是不是bootstrap！也是DP最大的一个特点。这就是为什么说TD综合了蒙特卡洛和DP的特点。

为了更好地说明，再来一个公式：

扫描二维码关注公众号，回复： 4073912 查看本文章

$v_{\pi}(s) &=&E_{\pi}[G_t|S_t=s]\;\;\;\;\;\;\;\;\;\;(1)\\&=&E_{\pi}[\sum_{k=0}^{\infty}{\gamma^kR_{t+k+1}|S_t=s} ]\\&=&E_{\pi}[R_{t+1}+\gamma\sum_{k=0}^{\infty}{\gamma^kR_{t+k+2}}| S_t=s]\\&=&E_{\pi}[R_{t+1}+\gamma v_{\pi}(S_{t+1})|S_t=s]\;\;\;\;\;(2)$

这是第三章讲贝尔曼方程时的公式。可以看出，蒙特卡洛算法是把（1）作为估计目标，然而expect return是不知道的，因此蒙特卡洛算法用每个样本的return来近似代替；DP把（2）作为估计目标，然而 $v_{\pi}(S_{t+1})$ 是不知道的，于是就拿之前的估计值代替；TD则是两个方式都用了：首先它用了采样的方式来算（2），其次用之前的估计值 $V(S_{t+1})$ 来代替真实的 $v_{\pi}(S_{t+1})$ 。

下面给出TD(0)的伪代码：

从back-up方式来看，DP使用的是full-backup，它基于所有可能的后续状态分布；而蒙特卡洛和TD使用的是sample back-up，它只基于当前发生的唯一的后续转移情况。

6.2 Advantages of TD Prediction Methods

这一小节讨论一下TD的优点。TD集成了蒙特卡洛和DP的特点，但是这种集成是好是坏呢？有什么优势呢？

首先有一点很明显，就是TD比DP是有优势的：不需要环境建模，不需要那些复杂的转移概率。其次，TD比蒙特卡洛有优势的一点是TD无需等待episode结束，可以实时计算。这一点非常重要，因为有时候一个episode会特别长，或者对于连续性任务来说，压根就没有episode，这时候TD的即时性就非常重要。

但是这样就代表TD算法是可靠的吗？虽然TD保证了即时性，那么它有没有保证正确性呢？幸运的是这一点是成立的。当上面的step-size parameter $\alpha$ 恒定且足够小或者逐渐递减但是满足随即近似理论，最终的结果都是可以保证收敛的。随机近似理论第二章提到过：

$\sum_{k=1}^{\infty}{}\alpha _k(a)=\infty\;\;\;\;\;\;\;\;and \;\;\;\;\;\;\;\sum_{k=1}^{\infty}{}\alpha _k^2(a) < \infty$

随之而来的问题是：如果TD和蒙特卡洛算法都能最终收敛，那么谁更快呢？事实上，没有理论证明谁更快，但是在实际的随机任务中，通常TD会更快一点。

我们在此给出一个例子，直观感受一下TD和MC的算法特点。

『例』
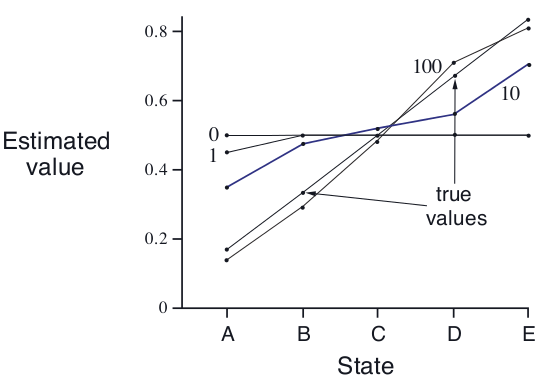
我们把这个例子叫做“random walk”，随机走动，从C开始出发，往左往右走的概率相同，只有到达最右侧reward是1,其他状态都是0。为了直观比较这两种算法对于value function的估计值和真实值的误差，我们需要知道真实value。這個例子故意特殊设计，使真实value很好算：每个状态的真实value就是从该状态起，到达最右侧的概率。于是 $v(A)=1/6$ ; $v(B)=2/6$ ; $v(C)=3/6$ ; $v(D)=4/6$ ; $v(E)=5/6$ 。一些实验结果如下：
上图是固定 $\alpha =0.1$ 情况下，随着episode数量增加，TD的估计值逐渐逼近真实值。
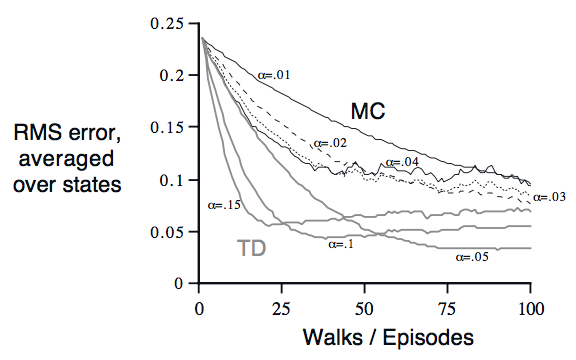
下图是当取不同的 $\alpha$ 时，TD和constant- $\alpha$ MC的误差收敛曲线随着episodes数量的变化趋势.

6.3 Optimality of TD(0)

这一节讨论一下TD(0)算法最优解的特点以及和蒙特卡洛最优解的比较

（ps:这一节说的TD都特指TD(0)算法,MC都特指constant- $\alpha$ 蒙特卡洛算法）

在之前我们谈到的两种算法的更新规则都是单次的，也就是说，对于MC算法，每个episode结束之后更新一次value；对于TD,每个time step都更新一次相应state的value。根据前面的random walk案例，可以看出随着 $\alpha$ 的不同，MC和TD每次的收敛结果都不一样,我们先记住这个结论，后面要对比。

现在我们引入另外一种更新规则：“batch updating”。因为在实际问题中有时并没有很多episodes，很可能我们手里就只有十几个episodes，这个时候，如何进行TD或者蒙特卡洛呢？我们可以把所有这一批episodes中关于每个state的更新增量，全部算完加和，然后更新一次value function。然后再走一遍所有的episodes，用新的value function再算一次增量和，再更新一次value function，直到value 收敛。

注意，注意，在这种“batch updating”操作下，TD算法的收敛结果却不受stepsize $\alpha$ 的影响，只要 $\alpha$ 足够小，每次batch updating的结果都一样，这个结论和前面TD在常规更新规则下的结论不一样。但是在constant- $\alpha$ 蒙特卡洛算法中，收敛结果在两种更新规则下均不确定。为了更好地理解这两种不同的结论，我们看两个例子，一步步来解释清楚两种算法背后的机制的不同。

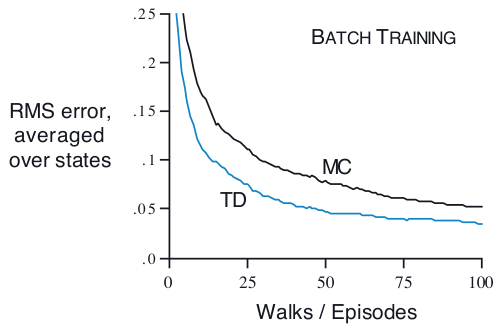
「例1」“batch updating”版本的random walk 在“batch updating”版本的“random walk”游戏里，有一点很不一样：每一个新产生的episode，都会和之前所有经过的episodes一起算作新的batch，然后整体更新value。这个更新设置是为了凸显MC和TD之间某种本质的不同。
下图给出了这种更新情况下，MC（蒙特卡洛）算法和TD算法的收敛误差比较，可以直观看出，TD全方位无死角秒杀MC：
RMS error指的是“root mean-squared error”，也就是“均方根误差”。从图中可以看出，随着新加入的episode不断增加，TD的效果一直保持比MC强。

在batch updating操作下，从不断减小估计值和真实训练数据之间的误差这个角度来说，MC的value估计可以说是最优的。但是很明显TD的效果一直比MC好，为什么TD竟然能比MC的最优估计还要好？原因是MC的最优是有限制的，而TD的最优更适合这种“不断添加新数据”的更新规则。

为了更好地说明上述结论，我们再来看一个例子：

「例2」
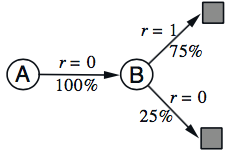
假如我们有8个短episode，分别是
拿第一个来说，就是A状态转移到B状态，reward是0，B状态转移到终止状态，reward也是0。现在问题是V(A),V(B)分别是多少？很显然，V(B)=3/4，这个毫无疑问，但是V(A)呢？有的人说既然A状态转移到B状态的概率是100%，而B状态的value是3/4，那么毫无疑问，A状态的value也是3/4。完美！看起来是对的，还有别的答案吗？有的人又说了，V(A)也可能是0啊，因为根据MC的算法，所有的episode中，从A开始到episode结束的return就是0啊。嗯，也没问题啊。
那么这两个V(A)，究竟那个是对的？
答案是：都对，只是做法不同而已。前者是TD的做法，后者是MC的做法。
我们进一步仔细讨论一下。对于前者，其思路是这样的：

注意到这个图其实就是第三章提到的马尔可夫状态转移图。知道了V(B),构造了状态之间的转移关系，得到V(A),这其实对应的就是之前TD(0)公式的“差分”部分：
$R_{t+1}+\gamma V(S_{t+1})-V(S_t)$
对于后者，思路就是按照正常MC算法，算出真实return的均值，为0。诚然，在这个例子中，MC得到的估计值和真实值之间的误差是0，貌似是理想的。可是，面对新加入的episode，当进行“batch updating”时，你愿意得到那个答案呢？其实第一个才是更合理的，尽管它在当前的误差并不比MC小，但是它可以在新的数据加入时，逐渐得到更小的误差，它的泛化能力更强，也可以说TD能学到这批episode数据背后的规律。为什么呢？因为它引入了相邻变量之间的联系，说白了也就是引入了DP的bootstrap思想，而这个区别帮助TD找到了数据背后的规律。

这个例子很好的说明了MC和TD在算法机制上的不同。我们详细说一下：

MC可以在固定的训练数据上得到误差最小的估计值。从统计学角度讲，MC的估计值是无偏估计，也就是如果有无限的样本，MC最终的估计结果一定是正确的；然而对于不断增加的样本数，每一个新加入的样本，与其他已有样本之间都是相互独立的，由于episode的长度不一定，MC算法每次都要等到episode序列结束，在等待过程中会引入大量的不确定性，最终的估计结果则自然带有很大的波动，也就是方差会很大。
TD可以在不断增加的数据上更快地得到误差较小的估计值。仍然从统计学角度看，TD的估计值是有偏的，因为它使用了别的状态的value 估计来更新当前状态的value，如果别的状态的value不是真实值，那么自然会引入一些偏差；然而由于TD只需要一步之后的结果，因此引入的波动性很小。另外，根据上个例子的结论，可以看出TD可以学到当前数据相关的马尔可夫模型的最大似然估计：模型中状态间的转移概率，就是当前观测序列中的转移概率，模型中的期望reward，就是当前观测序列中reward的均值，并依据这个模型估计给出绝对正确的value。因为一旦模型是对的，那么value的估计值就一定是正确的。这个过程也叫做“确定性等价估计”，因为它等同于假定潜在模型是确定性的，而非近似的。

上述总结也能说明为什么TD要比蒙特卡洛快很多（batch updating下）。因为TD总是在更新成更匹配数据的模型，估计值也越来越准确；而MC的已有估计结果会收到下一个episode随机性的影响。这也能一定程度上解释为何之前NonBatch规则下TD也比蒙特卡洛快，因为虽然NonBatch规则下TD并不能获得“确定性等价估计”，但也可以认为是粗略朝这个方向在更新估计值。

从适用性来说，蒙特卡洛算法更适合非马尔可夫性质的任务，TD算法更适合具备马尔可夫性质的任务。蒙特卡洛算法要求episode必须是离散的且必须有terminate state，TD则没这个要求。

6.4 Sarsa: On-policy TD Control

这一节开始，我们用TD代替第五章的MC,仍然按照GPI模式，整合到整个policy iteration过程中。TD在这里扮演的角色和MC一样，是policy evaluation部分。同样的，TD算法也需要平衡exploration和exploitation，因此也分成on-policy和off-policy两类。这一节是讲on-policy，下一节讲off-policy。

第一步，就是用估算 $q_{\pi}(s,a)$ 代替 $v_{\pi}(s,a)$ 。结合如下更新公式：

$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)]$

可知，如果我们要更新某个状态-动作对 $(S_t,A_t)$ 的Q，需要一个五元tuple $<S_t,A_t,R_{t+1},S_{t+1},A_{t+1}>$ ,这也是Sarsa名字的来历（哈哈有意思）。

第二步，确保Sarsa可以收敛。同on-policy的蒙特卡洛算法一样，Sarsa的收敛条件也是当所有的state-action pair都被访问过无限次，因此需要采取Non-deterministic类型的 $\varepsilon -greedy$ 或者 $\varepsilon -soft$ policies。

依然是给出伪代码：

6.5 Q-learning: Off-policy TD control

Q-learning如果拿第五章的off-policy MC算法来对比，就更容易理解了。Q-learning最简单的形式是one-step Q-learning,定义如下：

$Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma \max_aQ(S_{t+1},a)-Q(S_t,A_t)]$

注意和on-policy TD的区别： $\gamma \max_aQ(S_{t+1},a)$ ,这表明在更新当前 $Q(S_t,A_t)$ 时，不再用当前已经发生的下一步 $S_{t+1},A_{t+1}$ （由behavior policy生成）,而是从target policy在 $S_{t+1}$ 时结合所有可能的 $a$ 得到的 $\{Q(S_{t+1},a)\}$ 集合中选出最大的那个Q。

Q-learning 伪代码如下：

6.6 Games, Afterstates, and Other Special Cases

这一节主要讨论一个叫做Afterstates的概念。

我们都知道state、state-action pair，那么afterstate和这两者的不同就是把这state和action合起来，构成一个afterstate集合。根据afterstate集合，又可以衍生出afterstate value function。

为什么要这么干呢？因为在很多棋类游戏比如tic-tac-toe中，（1）很多情况下，某个state经过某个action之后的状态是确定性的；（2）很多state经过不同的action之后，会得到同样的afterstate，而只维护一个afterstate就能够减少很多多余的state-action pair。

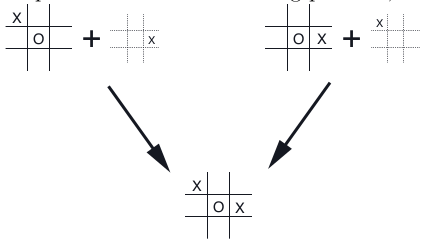
上图给出了tic-tac-toe游戏中一种典型的两种state-pair最后得到同一个afterstate的情况。

这种简化技巧可以减少agent的学习时间，还能应对某些不太容易使用state或者state-pair的任务。

强化学习导论 第六章 瞬时时间差分法

猜你喜欢

强化学习导论第六章瞬时时间差分法