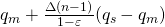强化学习导论第五章蒙特卡洛模拟

这一章讲蒙特卡洛方法在强化学习中的应用。

在这一章，我们将接触第一个用于估计value functions，并发现最优policies的方法。和前几章不一样的是，这次假设我们并非完全知道环境的动态信息（转移概率啦那些）。蒙特卡洛方法只需要经验知识，即：来自线上或者模拟环境交互过程的样本序列（包括状态序列、动作序列、奖励序列）。从在线的经验中学习非常酷，因为它不需要任何关于环境动态性质的先验知识，却仍然可以获得最优的行为表现；从模拟交互中学习也是一个很棒的办法。尽管这个过程仍然需要一个模型，但这个模型只是用来生成样本转移过程，而不是生成DP算法所必需的完整转移概率信息。令人惊讶的是：在很多情况下很容易按照想要的概率分布生成样本序列，然而却很难获得具体形式的概率分布。

蒙特卡洛方法基于样本返回值的平均化来解决强化学习问题。为了确保有定义明确的返回值概念，我们只在片段式任务上应用蒙特卡洛方法，也就是说所有的经验都被分成片段，并且所有的片段最终都会结束。只有当一个片段结束了，value的估计值和policy才能改变。因此蒙特卡洛方法是基于episode为单位的，而非step。“蒙特卡洛”这个词被广泛用在利用大量随机元素作估计的地方。在这里我们用它来表示基于完全return平均值的方法（和下一章讨论的从部分return中学习的方法相反）。

尽管蒙特卡洛方法和DP方法之间存在不同，但是DP方法的思想却仍然可以迁移到蒙特卡洛方法。我们不仅需要计算相同的value function，实质上也是通过相同的方式得到最优解。正如在DP那一章一样，在考虑第一个policy evaluation时，我们针对某个任意的policy $\pi$ 来计算 $v_{\pi}$ 和 $q_{\pi}$ ,然后进行policy improvement，最后得到通用性的policy iteration。这些思想都可以沿用到蒙特卡洛方法中，虽然仅仅只有样本经验数据。

5.1 Monte Carlo Policy Evaluation

我们现在开始考虑使用蒙特卡洛方法，基于一个给定的policy学习state-value function。回忆一下某个state的value指的是从当前状态开始的期望返回值--即长远累计的discounted奖励的期望值。从过往经验数据估计该值的一个很明显的方法，就是对所有访问过该状态之后的返回值进行平均化处理。随着更多的returns被观测到，其平均值最终会收敛于期望value--这就是蒙特卡洛方法暗含的思想。

具体来说，假如我们已知一个片段过程集合，这个集合中的每个片段过程都是依据policy $\pi$ 生成，并且都经过了state $s$ ，我们希望以此来估计 $v_{\pi}(s)$ ，也就是在policy为 $\pi$ 的时候，state $s$ 的value。一种名叫“every visit”的蒙特卡洛方法把整个片段集中所有访问到 $s$ 状态时的returns取平均，来估计 $v_{\pi}(s)$ 的值。与之相对应的还有一种名叫“first visit”的蒙特卡洛方法，它则是把整个片段集所有第一次访问到状态 $s$ 时的returns做平均化处理，来估计 $v_{\pi}(s)$ 的值。这两种方法非常相似，但是在理论性质上略有不同。后者（“first visit” method）的研究更加广泛，可以追溯到19世纪40年代，也是我们这一章的重点。我们也将在第七章再次讨论"every visit"方法。First-visit MC的过程形式如下图：

上述两种方法随着对状态 $s$ 的访问次数趋于无穷大，其最后结果都会趋于 $v_{\pi}(s)$ 。这个结论很容易在first visit MC方法中看出来：在这种情形下，每一个return都是独立同分布的 $v_{\pi}(s)$ 的估计值。根据大数定律，这些估计值的平均值序列将会收敛于它们的期望value。每一个估计值本身都是无偏估计，它的误差的标准差会依照 $1/\sqrt{n}$ 下降，其中 $n$ 表示待平均的returns的数量。every visit MC方法在这方面不太直观，但是它的估计值也会渐进收敛到 $v_{\pi}(s)$ 。

[Example 5.1]

这里的例子给出了21点，也就是blackjack，目的是为了说明为什么在这个游戏中不能用DP，而是要用蒙特卡洛思想。21点游戏的规则大家自己了解，用蒙特卡洛不用DP解决这类问题的原因主要是model很难准确建立。在21点中，玩家和庄家手牌的状态转移方式有非常多的可能性，很难一一计算概率。然而我们却很清楚的知道environment knowledge，这是很神奇的事情：我们明明知道很多环境的变化规则，但是却往往得不到可以应用的transition probility。

另外，我们可否把反向图的思想也用在蒙特卡洛算法这里呢？答案是可以的。反向图的顶端根节点是当前待更新的，根节点以下的部分是所有可能的转移状态（叶子节点），这些节点的reward和value对顶端根节点的value更新有帮助。对于使用蒙特卡洛方法更新 $v_{\pi}(s)$ 来说，根节点是一个状态节点，之后就是沿着某个特定片段过程的所有转移序列，最后是一个终止状态。如下图所示：

扫描二维码关注公众号，回复： 4073916 查看本文章

DP算法和蒙特卡洛算法的反向图的不同之处在于：（1）前者显示了所有可能的状态转移情况，而后者是显示某个样本片段中的转移情况（这里解释以下：DP是考虑了所有的状态转移可能性，尽管这些可能性都还没有发生；而蒙特卡洛是实实在在发生的某一种情形。可以用平行宇宙和现实宇宙的对比来类比）。（2）前者只是一步内的转移情况，而后者是所有步骤的转移情况。这两种区别精确反映了这两种算法之间根本的差异性。

蒙特卡洛算法一个重要的事实就是对每个状态的估计值是相互独立的。对某一个状态的估计并不建立在任何其他状态的估计之上，而DP就是这里所说的不独立--即对某一个状态的估计建立在任何其他状态的估计之上。换句话说，蒙特卡洛方法并不进行“bootstrap”。

特别的是，我们注意到对单一某个状态的value估计值的运算开销是独立于状态的总数的。这个特性使得蒙特卡洛方法变得尤其有优势，特别是当我们只需要一部分状态的value的时候。我们可以生成很多从这些需要的状态开始的样本片段过程，只对这些我们感兴趣的状态做returns的平均，忽略其他状态。这也是蒙特卡洛方法的第三个优势（前两者分别是蒙特卡洛方法可以从实际经验过程学习，也可以从模拟经验过程学习）。

5.2 Monte Carlo Estimation of Action Values

这一节我们主要讨论使用蒙特卡洛方法对Action Values,也就是 $q_{*}$ 的估计。首先有个问题是：为什么要讨论蒙特卡洛方法对Action Values的估计呢？这里的决定性因素是环境model的有无。

分两种情况来看：

<1> 有环境model。也就是我们知道环境状态的转移概率和reward。这样的话，我们只需要往前多看一步，看看那个action可以得到最优的reward+next state组合（回忆贝尔曼方程）就行了，和DP中的做法一样。这种情况下无需估计 $q_{*}$ 。

<2> 没有环境model。这种情况下，我们不知道环境的转移概率和相应的reward，也就是说我们没办法算那个贝尔曼方程右侧的迭代。因此我们只能去通过直接估计每个action和state的结合会得到多大的value，以此来决定policy。这种情况下必须估计 $q_{*}$ 。

因此，蒙特卡洛方法中的一个重要目标，就是如何估计 $q_{*}$ 。如何呢？其实和前一节提到的估计 $v_{\pi}(s)$ 的方法很相似，就是目标换成了 $q_{\pi}(s,a)$ 。方法依然是我们熟悉的“every visit”和“first visit” 两种。分别说一下：

(1) "every visit"：这个方法关注整个样本片段集合中所有在访问状态 $s$ 时选择动作 $a$ 的returns，然后求平均值，以此来估计 $q_{\pi}(s,a)$ 。

(2) “first visit”：顾名思义，这个方法只关注每个片段过程中第一次访问状态 $s$ 并选择动作 $a$ 的return，然后求平均值，以此来估计 $q_{\pi}(s,a)$ 。

这两种方法随着对每一对“state-action”访问次数趋于无限，都会收敛到真实 $q_{\pi}(s,a)$ 。

然而我们需要考虑一个严重的问题：在所有样本片段集合中，很多“state-pair”对并不出现，比如当我在一个确定的policy下，有可能某个state下只出现有限的几个对应的actions，其他的actions都基本不出现。这样我们根本没有returns去average，怎么能估计到某些 $q_{\pi}(s,a)$ 呢？

为什么这个问题严重？因为我们之所以一开始讨论估计 $q_{\pi}(s,a)$ ，目的就是为了在面对某一个state时，没有model的帮助，从所有的可能actions中选一个最优的。现在我们都不能保证所有的actions都被考虑到，这个目的自然也不能达成了。

这个问题就是普遍存在的“maintaining exloration”问题。在第二章提到过一点。其实就是应不应该在exploitation的同时也exploration的问题。那么在这里为了更好的估计 $q_{\pi}(s,a)$ ，我们必须得确保一直进行exploration。如何做呢？一个直观的方法，就是让每个state-pair对都有一定的概率被选中作为每个片段过程的开始节点。这样我们就能保证随着片段样本数量趋于无限，每个state-pair对都会被访问到无数次。这是我们做的一个假设前提，叫做“exploring start”。

这个“exploring start”看起来解决了上述问题，但是解决得完美吗？可以推广到一般情况吗？No，这个方法虽然有一定的作用，但是当我们需要直接从与环境的交互中学习策略的时候，就不那么有帮助了。因为真实情况下我们是不能去指定开始节点的，如果真的出现了很多state-pair访问不到，也没办法指定。那么还有没有解决方案呢？答案是肯定的。我们可以从policy下手，也就是在policy的evaluation过程中，只考虑那些对所有actions选择概率都不为0的policy。在后面几节会讨论这种方法，但是现在先保留之前的“exploring start”假设。

5.3 Monte Carlo Control

做了前两节的铺垫，这一节我们来正是使用蒙特卡洛算法获得最优policies的近似。这也是自从DP那一章以来我们共同的目的。仍然要提到GPI（generalized policy iteration）这个词，它出现在前一章DP中。这也说明用蒙特卡洛方法估计最优policies的方法流程和DP是非常相似的：先更迭value function使之逼近当前policy的真实value function，然后基于更新后的value function进行policy improvement，直到最终policy基本不再变化。流程图如下：

需要注意一个点：中间不再是 $v_{\pi}(s)$ ,而是 $q_{\pi}(s,a)$ ，也就是action-value function。这个时候，我们仍然需要保证两个假设前提。第一个：观测到无限数量的片段过程；第二：保证“exploring start”。这俩前提保证我们可以为每个任意的 $\pi_k$ 计算出相应的 $q_{\pi_k}$ 。

接下来就是policy improvement。和之前的 $v_{\pi}(s)$ 不同，当我们estimate的是 $q_{\pi}(s,a)$ 时，就不需要额外的model来确定最优的action了，因为我们直接就可以根据下式来确定了 $\pi(s)$ ：

$\pi(s)=\arg\max_a q(s,a)$

这样在每次policy evaluation完毕的时候，都可以根据 $q_{\pi_k}$ 来确定 $\pi_{k+1}$ 。又根据（4.2）提到的policy improvement theorem，可知每次得到的 $\pi_{k+1}$ 都是在整体上优于 $\pi_k$ 的，除非它已经是最优policy了。因此，通过上述流程，我们就可以在没有model先验知识的情况下，只通过样本片段的历史经验，就可以最终得到最优policy。

然而还有一个小问题需要处理。读者也许还记得我们之前设置的两个假设前提条件，这两个条件有效保证了结果的收敛性。然而，为了获得更具实际意义的蒙特卡洛算法，我们必须抛弃掉这两个假设。现在我们集中考虑如何去掉“infinte number of episodes”假设。

其实上述“infinite number of episodes”问题也出现在DP中了（读者还记得吗，最后我们简化成了value iteration）。有两种方法解决这个问题：

(1) 设置一个极小误差范围，直到两次policy evaluation的差别小于这个误差，认为此次policy evaluation结束。这个方法可以有效保证收敛精度，但是需要的episodes数量不少，小规模问题还能行，大规模的就不可取了。

(2) 摈弃evaluation的完整性。其实就是使用value iteration的方式，把policy evaluation的episode数量减少到1个，每次evaluation一次之后，不管误差有多大，都进行policy improvement。

目前我们得到的蒙特卡洛方法只保留了一个基本假设前提：“exploring start”,算法伪代码如下：

上述这个算法就叫做“Monte Carlo with Exploring Starts”，也就是“Monte Carlo ES”算法。该算法保证了 $q_{\pi}(s,a)$ 一定会收敛到 $q_*(s,a)$ ,且独立于过程中的policy。

5.4 On-Policy Monte Carlo Control

上一节末尾我们讲到目前的“Monte Carlo ES”算法依然有一个小小的缺点，就是依旧需要一个“exploring start”的前提条件。那么有没有办法来去掉这个前提呢？有两种方法可以做到：一种叫做on-policy method，另一种叫做off-policy method。这一节先讲第一种：on-policy method。

on-policy method有什么特别的地方呢？它的一个重要特点就是非确定性。也就是说

$\pi(a|s)>0\; for\; all \; s \in S \; and \; a \in A(s)$

on-policy method有很多种变体，其中一种就是我们在第二章“多臂赌博机”中讨论过的 $\varepsilon -greedy$ policies。在这个方法中，所有非greedy actions被选中的概率为 $\frac{\varepsilon}{|A(s)|}$ ，greedy actions被选中的概率为 $1-\varepsilon +\frac{\varepsilon} {|A(s)|}$ 。 $\varepsilon -greedy$ 属于 $\varepsilon -soft$ policies其中之一，也是其中最接近贪婪算法的那个。（注： $\varepsilon -soft$ policies指的是对于所有states和actions， $\pi(a|s) \geq \frac{\varepsilon }{|A(s)|}$ ,其中 $\varepsilon >0$ ）。

为什么要使用这种概率化的方式呢？因为如果我们每次都确定性地选择最优的action来更新policy，那么很可能有大部分的action-state pair都没有在episodes中出现，这样最后的average return也不合理。可以证明，通过选用 $\varepsilon -greedy$ policy，可以优于或者至少和其余 $\varepsilon -soft$ 系列的policies一样好。为什么要强调这一点呢？因为非greedy actions被选中的概率并不确定，到底那一种最好是很重要的，这决定了最终会不会得到最优policy。证明如下：

令 $\pi'$ 为 $\varepsilon -greedy$ 的policy，也就是所有非greedy actions被选中的概率为 $\frac{\varepsilon}{|A(s)|}$ ，那么对于所有 $s \in S$ :

简单说一下第二行到第三行的推导，前面的都相同，只是比较 $\max_a q_{\pi}(s,a)$

$\sum_{a}^{}{}\frac{\pi(a|s)-\frac{\varepsilon}{|A(s)|} } {1-\varepsilon } q_{\pi}(s,a)$ 的大小。

根据 $\varepsilon -soft$ 的特点， $\pi(a|s) \geq \frac{\varepsilon }{|A(s)|}$ ，我们假设 $\pi(a|s) = \frac{\varepsilon }{|A(s)|} + \Delta$ ,为了公式清晰，令 $|A(s)|=n$ 。易得到下式：

这里假设(1)non-greedy actions有n-1个，greedy action有1个；

(2)且所有non-greedy的action-value都统一等于次大值: $q_{\pi}(s,a)=q_s$ ;

(3) $\max_a q_{\pi}(s,a)=q_m$ ;代入 $\sum_{a}^{}{}\frac{\pi(a|s)-\frac{\varepsilon}{|A(s)|} } {1-\varepsilon } q_{\pi}(s,a)$

之后可以得到其等于

这样就很明显了，上式第三行的大于等于号成立。（证毕）

根据policy improvement theorem，可知 $\pi'\geq \pi$ 。

再多说一句关于为什么需要找到 $\varepsilon -soft$ policies集合中最优的 $\varepsilon -greedy$ ：因为在之前的policy improvement过程中，我们是确定性地选择了唯一的greedy action，并证实了它是最好的policy。所以我们要确保在 $\varepsilon -soft$ 情形下，依然能够切实地获得policy的improvement，那么就需要彻底找到一个最佳的概率值（最终是 $\frac{\varepsilon}{|A(s)|}$ ）赋予non-greedy actions，使该policy的 $q_{\pi}(s,\pi(s))$ 最大。

最后给出这一节 $\varepsilon -soft$ on-policy 蒙特卡罗算法伪代码：

5.5 Evaluating One Policy While Following Another (Off-policy Policy Evaluation)

这一节的问题很有意思。之前我们在estimate $v_{\pi}$ 或者 $q_{\pi}$ 时，需要根据目标policy-- $v_{\pi}$ ，生成一系列episodes，然后再进行policy的evaluation和improvement。现在问题来了，假如我们仍然想estimate $v_{\pi}$ 或者 $q_{\pi}$ ，然而给定的episodes缺不是依据 $v_{\pi}$ 或者 $q_{\pi}$ 生成的，而是依据一个不同的policy $\mu \ne \pi$ ,怎么办呢？这里先给出几个名词： $\pi$ 叫做目标策略（target policy）， $\mu$ 叫做行为策略（behavior policy），而从behavior policy生成的episodes中学习target policy的过程，叫做off-policy learning。

（我想提醒各位读者的是，这里引入的off-policy的思想非常重要，甚至在后面几章都还有提及，是重头戏，希望大家可以重视。同时，既然很重要，其难度也不小，所以也要细细品味其中的内涵）

首先，我们要问个问题：好端端的，我们已经在前几节基本解决了使用蒙特卡罗算法来estimate $q_{\pi}$ 并获得optimal policy，为什么这里还要来谈off-policy的问题。这就要从上一节的蛛丝马迹中发现端倪。在上一节末尾，我们已经可以从 $\varepsilon -soft$ 的一类policies中找到最优的policy $\varepsilon -greedy$ 了，但是请注意限定词“ $\varepsilon -soft$ ”。其实，我们最终得到的policy，是在妥协了“exploring start”这个假设下的最优policy。为什么？因为我们必须需要这个假设，没有这个假设，一切蒙特卡洛算法的根基就无从谈起，这些内容读者们可以看上一篇，有详细的介绍。

于是，为了满足这个“exploring start”假设，on-policy方法就必须要一定概率地去选择一些次优actions。这也就提出了一个问题：能不能不去妥协“exploring start”假设，还是用之前的greedy策略，每次就选最优的action呢？这就是为什么要讨论off-policy的原因。

在off-policy方法中，我们有两种policy：一种用于产生episodes，是之前说的behavior policy，姑且叫做 $\mu$ ；另一种，就是target policy，它是依据episodes得到的value function，得到的greedy policy。behavior policy是已知的，target policy是未知的。为了能够从 $\mu$ 生成的episodes中估计 $\pi$ , $\mu$ 必然是随机的，也就是 $\mu (a|s)>0$ ，因为必须确保 $\pi$ 中的所有actions在 $\mu$ 中都出现。 $\pi$ 却可以是确定性的，因为我们想得到完全的最优解。也就是说，把exploration的任务交给 $\mu$ ，让它彻底地exploration，而从它产生的 $q_{\pi}$ 中，通过某种方式，使得 $\pi$ 可以保持彻底的greedy。

（高能预警，下面的这部分自我感觉比较难懂，但是尽量说明白。）

首先我们给出两个概率表达式，如下：

$p_{i}(S_{t})=\prod_{k=t}^{T_{i}(S_{t})-1} {\pi(A_{k}|S_{k})p(S_{k+1}|S_k,A_k)}$ $p_{i}(s_{t})=\prod_{k=t}^{T_{i}(s_{t})-1} {\mu(a_{k}|s_{k})p(s_{k+1}|s_k,a_k)}$

逐一分析： $i$ 表示第 $i$ 个episode序列；大写的 $S$ 和小写的 $s$ 为了区分在策略 $\pi$ 和策略 $\mu$ 下的序列；这两个式子分别表示在策略 $\pi$ 和策略 $\mu$ 下，第一次访问到状态s之后的两个相同序列的发生概率，注意是相同序列。假设把从state $s$ 开始观测到的return记作 $G_{i}(s)$ ,也就是说这个 $G_{i}(s)$ 是在behavior policy下观测到的，如果我们想要根据这个return来estimate $v_{\pi}(s)$ ,就需要满足下列式子：

$V(s)=\frac{\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}G_{i}(s)} }{\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}}}$

这里需要特比说明的有三点：第一，为什么求和？这个好解释，因为蒙特卡洛方法就是要作多次returns之后的平均；第二，为什么要求 $\frac{p_i(s)}{p_i^{'}(s)}$ ？这个原因要回顾一下上面的两个概率表达式。我们这么来想：假设有两个事件A和B，已知A发生的概率为 $p(A)$ ,B发生的概率为 $p(B)$ ,现在又已知A的某个相关变量 $f(A)$ ,那么怎么求B的那个相关变量 $f(B)$ 呢？其实这里A的相关变量就可以看成是 $G_{i}(s)$ ，B的那个相关变量就是要求的 $V(s)$ ，两者概率的相对比例和两个相关变量的相对比例是相同的。第三点，为什么要除以 ${\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}}}$ ，这个也好解释，为了归一化。

好了，还有一個问题，怎么得到 $\frac{p_i(s)}{p_i^{'}(s)}$ ？这个相对好解决：

要注意这里为什么最后可以约掉 $p(S_{k+1}|S_{k},A_{k})$ ,是因为前面强调的相同序列。只有在相同序列中，两种策略下的 $S_{k}$ 和 $A_{k}$ 才均相同，这样 $p(S_{k+1}|S_{k},A_{k})$ 才相同。从另一个角度看，如果不直接求两者的相对比例，而是去分别求出 $p_{i}(S_{t})$ 和 $p_{i}^{'}(S_{t})$ ,再试图相除，就做不到。因为蒙特卡洛算法面对的问题往往是不知道任何环境动态性质的，也正是因为我们没有这么做，才恰好利用了相同序列 $p(S_{k+1}|S_{k},A_{k})$ 可以消掉的性质，解决了求 $\frac{p_i(s)}{p_i^{'}(s)}$ 这个问题。

5.6 Off-Policy Monte Carlo Control

有了上一节的铺垫，这一节我们就可以看一下真正的off-policy 蒙特卡洛算法了。重新回顾一下Off-Policy的思想：使用 $\varepsilon -soft$ 类型的behavior policy来生成episodes，这些episodes经过了充分的exploration；从这些episodes中按照蒙特卡洛的“every visit”或者“first visit”方法计算 $G_{i}(s)$ ，然后根据 $V(s)=\frac{\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}G_{i}(s)} }{\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}}}$ 来计算target policy的 $v_{\pi}(s)$ 。off-policy的优点是分离了exploration和greedy action‘s choice这两个过程，而之前在on-policy算法中，它们必须相互妥协，使得最终效果不是很好。

程序应该怎么写呢？以下给出了伪代码：

解释一下伪代码中的几个重点：首先是小括号（b）那一句，latest time的含义，指的是，在这个时间点 $\tau$ 之后，所有的 $A_{\tau }=\pi(S_{\tau})$ ,也就是说只有这个时间点之后的序列，才能被用于计算target policy的 $Q(s,a)$ ,为什么？请读者结合前面的内容思考。然后是（c）那部分，为什么 $W\leftarrow \prod_{k=t+1}^{T-1} {\frac{1}{\mu (A_{k}|S_{k})}}$ ？因为在时间点 $\tau$ 之后的序列，两种策略的动作选择都是相同的，也就是说 $\pi(A_{k}|S_{k})=1$ ,因此分子是1。

这种方法是完美的吗？并不尽然，一个潜在的问题就是每个episode可利用的部分只有尾部，也就是只有在时间点 $\tau$ 之后的序列，即最后一个non-greedy action之后，才可以被用来更新 $Q(s,a)$ 。那么如果non-greedy actions特别多，会使得学习过程很缓慢。这个问题的严重性如何评估，需要进一步商榷。

5.7 Incremental Implementation

这一节主要讲的就是一个小的trick，回想一下第二节中讨论的多臂赌博机问题，那里提到了把return写成递增的形式。这一节也是讨论如何通过某种方式，把off-policy方法中的下式：

$V(s)=\frac{\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}G_{i}(s)} }{\sum_{i=1}^{n_{s}}{\frac{p_i(s)}{p_{i}^{'}(s)}}}$

写成递增的形式。这样写有个好处就是可以省内存和计算时间，因为随着episodes数量的增加，如果按照原写法计算，会不断增加内存的负担，也会不断增加计算量。而写成递增的形式，则无论episodes数量如何增大，我们始终只需要保存两个变量：原 $V(s)$ 和增量，就可以不断更新return了。

以下是数学推导，有兴趣的可以一看：

令 $W_k=\frac{p_{k}(s)}{p_{k}^{'}(s)}$ ,那么上式的 $V(s)$ 可以写成以下形式： $V_{n}=\frac{\sum_{k=1}^{n-1}{W_kG_k} }{\sum_{k=1}^{n-1}W_k}$ ,于是 $V_{n+1}=\frac{\sum_{k=1}^{n}{W_kG_k} }{\sum_{k=1}^{n}W_k}$ 令 ${\sum_{k=1}^{n}W_k}=C_n$ 那么 $V_{n+1}=\frac{C_{n-1}V_n+W_nG_n}{C_n}\\=\frac{(C_n-W_n)V_n+W_nG_n}{C_n}\\$ 最终可得： $V_{n+1}=V_{n}+\frac{W_n}{C_n}[G_n-V_n]$ $C_{n+1}=C_n+W_{n+1}$ $C_0=0$

5.8 Summary

按惯例，需要总结一下。蒙特卡洛方法的主要思想就是从过往的实际经验中学习策略。这些过往经验以若干独立的样本片段给出。这种独特的思想使蒙特卡洛方法拥有DP所不具备的三大优势：

(1)不需要环境的动态model。实际环境的model有时很复杂，很难准确建立。

(2)可以通过模拟样本片段来使用。很多情况下，精确的转移概率模型很难确立，但是往往很容易模拟样本的走势。

(3)可以有选择地专注于真正重要的一部分状态集合。

还有一個优势在后几章将会讲到，当环境的马尔科夫性质不能被严格满足时，使用蒙特卡罗方法比使用DP受到的影响小（这一点我暂时很难给出确切的说明，在后几章或许可以说的更明白一些）。这是因为蒙特卡洛方法不进行bootstrap，而DP需要bootstrap。

这里要说明一下bootstrap的含义：在统计学中，bootstrap常常表示在有些的样本中进行多次有放回抽样，以获得足够估计总体的样本数量。在这里指的是有没有通过估计的方法来引导计算，也就是自举。DP算法中，每次value的更新都需要之前的value估计值，而蒙特卡洛算法中就不需要这些。

蒙特卡洛算法的基本模式依然是GPI,先policy evaluation，然后policy improvement。其核心思想则提供了另一种policy evaluation的方法：不用model来递归计算所有可能性，而是对真实样本片段经验过程的returns平均化。我们通常估计 $q_{\pi}(s,a)$ 而不再是 $v_{\pi}(s)$ ,因为前者可以保证在没有model的情况下也能进行policy improvement。另外，蒙特卡洛算法也可以写成增量形式（前一节内容）。

蒙特卡洛算法中，保证足够的exploration是最需要注意的关键点。因为如果只是选择当前对应 $q_{\pi}(s,a)$ 的最优action，那么将会导致很多其他的actions永远没机会选到。一个解决方案是“exploring start”，这个方案在模拟产生episodes也许可行，但是在从真实经验中学习时就不可行了，因为我们无法控制start point。于是分化出了两种学习方式：on-policy和off-policy。on-policy方法一边exploration一边在此基础上选取最优解；off-policy则彻底把exploration和policy improvement过程彻底分开：更彻底地exploration，更彻底地选择greedy actions，最后得到的optimal policy甚至和behavior policy没有任何关系。

最后说一下蒙特卡洛算法和DP算法的不同：第一点：前者可以从样本经验学习，也就是说，它不需要任何准备模型的过程，可以直接在真实情形下学习，而后者必须有一个精确的模型；第二点：前者不需要bootstrap，也就是不基于其他value estimates来更新某个value，后者则是递归更新。

在下一章，我们会讨论这两种算法的某种意义上的结合体：既从经验中学习，又进行bootstrap过程。

强化学习导论 第五章 蒙特卡洛模拟

猜你喜欢

强化学习导论第五章蒙特卡洛模拟