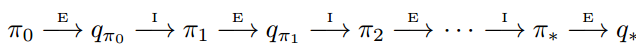[归纳]强化学习导论 - 第五章：蒙特卡洛方法

1.本章内容概要

这一章我们考虑第一种同时估计值函数和找到最优策略的学习方法。和之前不同，我们不再假设已知环境模型(这是实际中最可能的情况)，蒙特卡洛(Monte Carlo, MC)方法只需要和真实/仿真环境交互的经验(state, action, reward)就行了。从仿真环境中学习也是非常有价值的，此时我们只需要状态转移就行(transitions, s, r, s’)，很多时候这是容易的，但是很难获得四参数形式的环境概率模型。

MC方法是基于样本returns均值的，因此我们只考虑episodic任务，因为我们需要对在多个episodes中出现的s的returns取平均。只有在完整的episode结束后，才能用MC方法估计值函数和提升策略，因此MC方法是episode-by-episode的，而不是step-by-step(online)的。

MC方法采样并平均每个state-action对，类似于我们在multi-armed bandits中的做法，但是这里将有多个状态(associative or contextual)，因此每个state-action对的值与后续状态及策略有关，而因为我们可能不断在提升策略，因此本章讨论的问题也是nonstationary的。

MC方法是基于GPI的，但与DP不同，我们是利用和环境交互的样本来学习值函数的，然后在此基础上提升策略。类似地，我们也先讨论prediction问题，然后讨论策略提升问题，最后讨论基于GPI的control问题。

2.蒙特卡洛预测

我们考虑通过MC方法学习一个给定策略的state-value函数(回忆下，state-value是从当前状态开始的期望累积未来折扣回报(expected return))。很自然地，我们会考虑利用 $G_{t, i}(s)$的平均值作为state-value的估计。而为了计算returns，我们必须要等一个完整的episode结束才行。

我们根据策略 $\pi$生成一些episodes，状态s的每次出现都叫做对s的一次visit，而在一个episode中，状态s可能出现多次，也可能不出现。MC方法一般分为first-visit MC和every-visit MC，前者只考虑在一个episode中s第一次出现的return，后者则考虑所有。在理论上对first-visit MC研究较多，every-visit MC则能更容易地扩展到函数拟合方式(与表格法对应)和资格迹，后面会详细讨论，这里主要讨论first-visit MC。

两种MC都能收敛到 $v_\pi(s)$，只要保证每个s能visit无数次，这对于first-visit MC是显而易见的，因为不同i时 $G_{t, i}(s)$独立，且均值是无偏估计，估计的标准差按照 $1/\sqrt{n}$下降；对于every-visit MC，则也已经有研究者给出了分析，其二次地收敛到真值。

example 5.1 Blackjack
就是21点问题。所有的花牌(face cards)都当作10点，王牌(ace)可以当作1点或者11点，其它牌就根据其数字大小，如果谁的点数之和超过21点(bust)则就输了；否则谁的点数之和接近21点就获胜。游戏开始庄家(dealer)和玩家(player)各发 2 张牌，庄家的牌一张向上一张向下，如果任何人没有出现21点(natural)[出现的话21点的一方获胜]，player和dealer可轮流决定是否拿牌(hits or sticks)。dealer的策略我们固定住，如果小于17就hits，否则sticks。
这是一个典型的episodic finite MDP，记player胜利，失败，平局的reward分别为+1，-1，0，不折扣。player动作空间 $A(s)\in \{hits, sticks\}$，状态则有三个维度，手牌的大小、dealer正面牌的大小、手中是否有王牌(只要不bust就当作11)，我们假设牌堆中各种牌的比例始终不变，根据这三个维度的状态决策。
对于player，我们也设定固定的策略：大于等于20就sticks，否则就hits。采用MC方法估计各个状态的值，注意包含王牌的情况收敛得更慢一些，因为这些状态更罕见。手牌点数我们从12开始考虑，因为小于12肯定是要hits的。在这个问题中 first-visit MC 和 every-visit MC 是一样的，因为在一局游戏中不可能出现两个相同的状态。那么，你能解释图中一些现象的原因吗？

在example 5.1中，虽然我们有任务的完整模型，但是我们还是无法应用DP方法，因为计算 $p(r,s'|s,a)$很困难。但是MC方法不需要四参数环境模型，因此能更轻松地解决这类问题。

我们可以画出MC方法的backup diagram。

MC方法的backup diagram实际是一条从开始到终止的轨迹，只用samples更新，而DP方法则需要在每个状态上考虑所有的后续状态，且只包含one-step transitions。且MC独立地估计每个值，而DP是bootstrapping的，并不独立。

MC方法的优势：

1. 单个状态的值估计的计算代价与状态数量之间独立，因此可以只处理我们感兴趣的状态；
2. 可以从实际经验和仿真经验中学习；
3. 不需要完整的环境模型；
4. 无偏。

example 5.2 Soap Bubble
一个不规则的铁丝框，放到肥皂水里拿出来，会产生一个薄膜，不考虑重力，如何计算薄膜上指定点的高度(薄膜的形状)？我们考虑约束：某个点的高度是临近一个小圆内的点的高度的平均。则可以把这个区域划分为网格，然后把线框上的格子的高度约束在线框的高度上，然后迭代计算各个格子的高度(每个格子高度为周围四个的平均)。

这个问题是MC方法最初被设计的目的。如果我们只对某个点或者区域感兴趣，我们就从这个点出发，以1/4的概率随意选择方向，直到碰到边界返回边界的高度作为reward，其它位置的reward设为0。然后无折扣地，我们就可以通过这个点或者区域的状态值的平均估计高度了。

3.动作值的蒙特卡洛估计

如果我们没有四参数模型 $p(r,s'|s,a)$(这是很常见的)，则只有state value函数就不够了，因为我们无法得知当前状态下采取动作后状态会如何变化，因而就无法去选择那个导致值最大的动作：

$\max\limits_a\sum_{s',r}p(s',r|s,a)[r+ \gamma v_*(s')]$

因此我们必须评估action value函数 $q_\pi(s, a)$。评估action value函数类似于评估state value函数，不过是考虑成state-action对，我们把对state-action对的visit的return取平均。action value的MC方法的收敛性与state value情形类似，且也分为first visit与every visit两种方法。

通过MC方法估计动作值函数，估值量会上升到 $|S|*|A|$，而且很多状态-动作对可能永远不会被visit，尤其是 $\pi$是确定性的时候这个问题尤其严重，这就很难指导我们提升策略了(策略提升要求我们对状态s下所有的state-action对的值函数都估计地较准确)。因此必须想办法计算所有的state-action对的值，这叫做maintaining exploration问题。解决办法：

1. exploring starts：指定从某个(s, a)开始，保证以所有的state-action对开端的概率不为0，后面再按照策略选择和计算。这在和实际环境交互学习时无用，且可能会组合爆炸；
2. 采用随机策略保证每个(s,a)都有出现的概率(ε-greedy也是可行的)。

本章后面的讨论暂时假定采用exploring starts的方式。

4.蒙特卡洛控制

control指得到最优策略的过程。后面我们把值函数估计都叫做prediction，策略提升叫做improvement，把prediction与improvement的配合叫做control。类似于DP，我们也从GPI(参见上一章)出发。回顾上一章的内容，GPI的过程为：

evaluation与improvement相互竞争，每个都为对方创造了一个移动的目标，但是合在一起导向了全局最优的值函数与全局最优的策略。

MC评估值函数需要多个完整的episodes，因此如上图，首先从初始策略 $\pi_0$出发，仿真多轮得到a complete policy evaluation(收敛) $q_k(s, a)$，在此基础上利用策略提升方法 $\pi_{k+1}(s) \doteq \arg \max_a q(s,a)$，得到a complete policy improvement(每个state都greedy地选择动作)，反复迭代直到收敛。之所以在策略提升中greedy，是因为：

$\begin{aligned} q_{\pi_k} (s, \pi_{k+1}(s)) &= q_{\pi_k}(s, \arg \max_a q_{\pi_k}(s,a)) \\ &= \max_a q_{\pi_k}(s,a) \\ & \geq q_{\pi_k}(s, \pi_k(s)) \\ & \geq v_{\pi_k}(s) \end{aligned}$

上述推导中，应该留意最后一步为什么成立。这是因为如果策略是soft的，那么 $v$应该是比 $q(s, \pi_k)$小的。

因而满足上一章介绍的策略提升定理。因此可见，MC方法不需要环境模型就能找到最优策略。

但是这其中有两个要求：任务可以进行无限多的episodes；并且结合exploring starts保证探索性。显然这两个假设都不太现实。为了得到一个实际可行的策略，我们必须去掉这两个假设。我们先来解决第二个假设，第一个假设留到下一小节，有两种解决办法，这两种方法都是参考自DP的policy iteration与value iteration的：

1. 类似policy iteration中的方法，保证每次估计误差(更新量)在一定范围内就行；
2. 放弃准确估计值函数，类似value iteration中的方法，只让值函数向着真值前进一小步，就开始提升策略。这应该比第一种效率更高。

这两种办法的有效性由GPI保证。第二种方法如果按照episode-by-episode执行，就是每个episode进行一次Bellman最优迭代更新，则算法称为：MC with Exploring Starts，MCES。

关于算法的几个注意事项：

1. 这是first-visit的，因此unless那句的含义是，只有在 $S_0, A_0, ..., S_{t-1}, A_{t-1}$中不包含 $S_t, A_t$对时，才执行。
2. 该算法可以容易地改成迭代的形式，这样就不必为了求均值保存所有的returns了。
3. 第一/二章中我们说明了非平稳过程问题(本算法就是，因为策略一直在变化)，我们应该更信任最近的returns，而上述算法中是直接平均的，但是当算法循环无穷episodes时，前面不准确returns的影响会被稀释掉，因此也能达到全局最优。这个全局最优不动点看起来一定会达到，但是到现在为止却还没有完全证明。

example 5.3 Solving Blackjack
回到21点问题。随机初始化(无论什么状态hits/sticks都等概率，回忆下状态实际上有三个维度)，值函数最初都设置为0，然后利用上面的方法寻找最好的策略，下图展示了这个版本21点问题的最优策略。

5.无探索性起点的蒙特卡洛控制

如何避免MCES的exploring starts假设呢？只要保证能无限地持续选中它们就行了，有两种策略：on-policy和off-policy。on-policy指产生样本的策略(behavior policy)和被估计的策略(target policy)是同一个策略，而off-policy则指behavior policy与target policy不同。MCES可以基于on-policy扩展，从而不依赖exploring starts，也可以根据off-policy扩展。我们这一节讨论on-policy情形。

on-policy去除exploring starts的方法是：保证每个状态下所有动作的被选概率都不为0(soft-policy)，即 $\pi(a|s) > 0$，且逐渐地趋近于最优确定性策略，第二章我们讨论了很多达成这个目的的办法，这里我们采用 $\epsilon-greedy$方法，即以 $1-\epsilon+\frac{\epsilon}{|A(s)|}$的概率选择greedy动作，以 $\frac{\epsilon}{|A(s)|}$的概率选择其它动作。 $\epsilon-greedy$策略是 $\epsilon-soft$策略的一种，而 $\epsilon-soft$要求 $\pi(a|s) \geq \frac{\varepsilon}{|\mathcal{A}(s)|}$。ε-greedy是ε-soft策略中比较趋近于greedy的一种。

soft-policy， $\epsilon-soft$和 $\epsilon-greedy$的关系如下图[1]：

基于on-policy的不需要exploring starts的first-visit MC方法，也是在GPI框架下的。基于GPI和ε-greedy，我们最终能得到一个还不错的策略，我们可以让 $\epsilon$的值逐渐降低从而得到全局最优策略。

注意算法中初始化策略为任意 $\epsilon-soft$策略，那么为什么 $\epsilon-greedy$能改善它呢？这里证明一下：

$\begin{aligned} v_{{\pi}'}(s) &= \sum_a \pi'(a|s) q_\pi (s,a) \\ &= \frac{\varepsilon}{|\mathcal{A}(s)|} \sum_a q_\pi (s,a) + (1-\varepsilon) \color{red} { \max_a q_\pi (s,a) } \\ & \geq \frac{\varepsilon}{|\mathcal{A}(s)|} \sum_a q_\pi (s,a) + (1-\varepsilon) \color{red} {\sum_a \frac{\pi(a|s) - \frac{\varepsilon}{|\mathcal{A}(s)|}}{1 - \varepsilon} q_\pi (s,a) } \\ &= \frac{\varepsilon}{|\mathcal{A}(s)|} \sum_a q_\pi (s,a) - \frac{\varepsilon}{|\mathcal{A}(s)|} \sum_a q_\pi (s,a) + \sum_a \pi(a|s) q_\pi(s,a) \\ &= v_\pi(s) \end{aligned}$

其中，不等号那一行之所以成立，是因为：

$\color{red} {\sum_a \frac{\pi(a|s) - \frac{\varepsilon}{|\mathcal{A}(s)|}}{1 - \varepsilon}} = \frac{1}{1 - \varepsilon} \left[ \sum_a \pi(a|s) - \sum_a \frac{\varepsilon}{|\mathcal{A}(s)|} \right] = \frac{1}{1 - \varepsilon}[1 - \varepsilon] =1$

这相当于对 $q_\pi(s, a)$加权(其中每一项 $\frac{\pi(a|s)-\frac{\epsilon}{|A(s)|}}{1-\epsilon}\geq0$)，肯定是小于 $\max\limits_aq_\pi(s,a)$的。

因而策略得到了改善。

我们可以换一种角度理解上述内容。我们把 $\epsilon-soft$移动到环境中去得到新的环境，新环境与旧环境的动作集合与状态集合是一致的。如果在状态s下采取动作a，那么新环境按照1-ε的概率按照旧环境那样反应，以ε的概率按照随机的其它动作那样反应。在这个环境中我们能得到的最优策略与在旧的环境中直接采用ε-soft得到的最优策略是一样。令 $\widetilde{v}_*$和 $\widetilde{q}_*$表示新环境下的最优值函数，那么根据最优值函数的定义，有：

在旧环境中，当 $\epsilon-soft$策略不能再提升的时候，满足：

也就是，在旧环境中通过 $\epsilon-soft$方法收敛到的不动点与在新环境中根据最优Bellman方程得到的策略是一样的。而因为 $\widetilde{v}_*$是唯一的，因此 $v_\pi$也是唯一的。

这种角度实际上说明了policy iteration在ε-soft策略下也是work的。且能收敛到soft下的最优。通过这样的方式，就可以去掉exploring starts的假设了，虽然只达到了ε-soft下的最优策略。

6.基于重要性采样的off-policy预测

所有的学习控制方法都面临一个困境：计算最优值函数需要按照最优动作运行，但是为了找到最优动作又需要探索非当前最优策略。那么能不能在保证探索的同时还能得到最优值函数呢？on-policy是妥协的方案，只找到了次优的值函数，这里我们介绍off-policy方法：同时采用两个策略，一个叫做target policy，这是被学习的最优策略，它是确定性的；一个叫behavior policy，这是产生行为的策略，它是soft的。

on-policy原理上比较简单；off-policy则稍微复杂，且具有更大的方差和更慢的收敛速度，但是off-policy更通用和有力，实际上，on-policy是target=behavior的off-policy特殊形式。此外，off-policy还可以利用专家经验数据与非学习控制器，且是学习多步预测世界模型的关键。

我们用 $\pi$表示target策略，用 $b$表示behavior策略，其用来生成轨迹。这两个策略暂时认为是给定的不变策略。为了使得 $b$能够估计 $\pi$，要求每个 $\pi$可能采取的动作，必须被 $b$覆盖(覆盖假设, 也就是所有只要 $\pi(a|s)>0$，必须有 $b(a|s)>0$)。注意这里 $b$和 $\pi$不完全一样，target可以是确定性的，behavior可以带有随机性保持探索。

off-policy基于重要性采样(importance sampling)，即通过一个分布的样本估计另一个分布的期望值。利用target和behavior策略轨迹的相对概率加权returns。这叫做重要性采样比率(importance-sampling ratio)。给定一个起始状态 $S_t$，则在策略 $\pi$下，轨迹 $A_t, S_{t+1}, A_{t+1}, ..., S_T$出现的概率为:

$Pr \{ A_t, S_{t+1}, A_{t+1}, \dots, S_T | S_t, A_{t:T-1} \sim \pi \} \\ = \pi(A_t| S_t) p(S_{t+1} | S_t, A_t) \color{red} {\pi(A_{t+1 } |S_{t+1})} \cdots p(S_T | S_{T-1}, A_{T-1}) \\ = \prod_{k=t} ^ {T-1} \pi(A_k | S_k) p(S_{k+1}|S_k, A_k)$

因此，我们就能得到behavior policy和target policy各自产生这条轨迹之概率的比值，该比值就是重要性采样比率，且该比率与MDP联合条件概率无关(也就是不依赖模型)，只与两个策略有关：

$\rho_{t:T-1} \doteq \frac{\prod_{k=t}^{T-1} \pi(A_k | S_k) p(S_{k+1}|S_k, A_k)} {\prod_{k=t}^{T-1} b(A_k | S_k) p(S_{k+1}|S_k, A_k)} = \prod_{k=t}^{T-1} \frac{\pi(A_k|S_k)}{b(A_k|S_k)}$

我们根据behavior policy得到样本，因此计算出的 $G_t$是关于behavior policy的，我们不能直接用它的期望估计target policy的值，但是如果乘上重要性采样比率，那么就可以转化为对target policy的值的无偏估计，其中 $\rho_{t:T-1} G_t$叫做scaled returns：

$\mathbb{E}[\rho_{t:T-1} G_t | S_t =s ] = v_\pi (s)$

接下来我们给出off-policy的MC算法。为了简便，我们打通episodes，例如，第一个episode的step编号是1~100，那么第二个episode的step号就从101开始。我们用 $J(s)$表示在每个episode区间，状态s被first-visit的step； $T(t)$表示step t对应的那个episode的终止step； $G_t$表示从 $t$到 $T(t)$的return； $\{G_t\}_{t \in J(s)}$表示状态s的所有returns， $\{\rho_{t:T(t)-1}\}_{t \in J(s)}$表示对应的重要性采样比率。我们可以构造两种基于重要性采样的 $v_\pi(s)$的估计：

ordinary importance sampling: $v_\pi(s) \doteq \frac {\sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1} G_t} {|\mathcal{J}(s)|}$

weighted importance sampling: $v_\pi(s) \doteq \frac {\sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1} G_t} {\sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1}}$

我们介绍下这两种方法的区别：直观看，ordinary是无偏的，weighted是有偏的(渐进无偏，可以直观理解，当episodes数目趋近于 $\infty$时， $|J(s)|=\sum_{t\in J(s)}\rho_{t:T(t)-1}$)；ordinary方差大(因为 $\rho_{t:T(t)-1}$波动大)，weighted方差小(归一)。考虑first-visit情况，如果某个s只出现一次的话，对于weighted方法，分子分母的 $\rho_{t:T(t)-1}$就被消掉了，这样就变成估计 $V_b$了；ordinary是无偏的，但是容易极端，例如ratio是10，则认为观察到的轨迹在target policy下比behavior policy下出现的可能性高10倍，这会把return放大10倍，导致方差变大。

这两种方法的区别在于方差和偏差。对于方差，显然ordinary方法是无界的，但是weighted方法是有界的，加权因子最大不超过1，实际上weighted的方差是收敛到0的，即使重要性采样比率无界；对于偏差，ordinary无偏，weighted方法渐进无偏。因此，我们往往倾向于weighted方法，但是ordinary方法更容易扩展到函数拟合的方法族中。

注意，对于every-visit情形，两种方法都是有偏的，但是都渐进收敛到0。every-visit是更常用的，这样就不需要记录每个状态的轨迹，且更容易扩展到拟合器的方法族。

example 5.4
仍然是21点问题，我们只评估一个特定状态的值(dealer翻出的牌是2点，player的总点数是13，有一个可用的ace)。利用off-policy方法评估这个状态的值函数。这里首先设定了一个target policy和一个behavior policy，然后利用weighted方法和ordinary方法分别计算，画出均方误差曲线(MSE curve)，发现weighted方法在次数较少时确实方差小很多，两者都收敛到最优。

example 5.5 Infinite Variance
如下图右上角的转移图所示，共两个状态，方框表示终止状态。在s下有两个动作，right导致100%通向终止，left导致10%通向终止。各种情况的Reward如图所示。target policy总选择left，取 $\gamma$=1，可以分析出 $v_\pi(s)=1$，behavior policy则平均选择left和right。

图中的曲线是利用ordinary方法运行10轮仿真得到的，每轮仿真进行100,000,000个episodes。可以看到，即便这么多次episodes还是没能收敛到真实值，而且时不时出现很差的值。这实际上是由于 $Var[\rho_{t:T-1} G_t | S_t =s ] = \infty$引起的，下面我们进行说明：

1. 首先给出方差的展开式：
   $\operatorname{Var}[X] \doteq \mathbb{E}\left[(X-\overline{X})^{2}\right]=\mathbb{E}\left[X^{2}-2 X \overline{X}+\overline{X}^{2}\right]=\mathbb{E}\left[X^{2}\right]-\overline{X}^{2}$
2. 我们把 $X$替换为scaled returns $\rho_{t:T-1} G_t$，按照不同episode出现的概率展开，有：
   $\begin{aligned}\mathbb{E}_{b}[X]&=\mathbb{E}_{b}\left[\prod_{t=0}^{T-1} \frac{\pi\left(A_{t} | S_{t}\right)}{b\left(A_{t} | S_{t}\right)} G_{0}\right]\\&=\frac{1}{2}\cdot0.1\cdot(\frac{1}{0.5})+\frac{1}{2}\cdot0.9\cdot\frac{1}{2}\cdot0.1\cdot(\frac{1}{0.5})^2+...\\&=0.1+0.1\cdot0.9+...+0.1\cdot0.9\cdot0.9+...\\&=0.1\cdot\sum\limits_{k=0}^{\infty}0.9^k = 1.0\end{aligned}$
   $\begin{aligned}\mathbb{E}_{b}[X^2]&=\mathbb{E}_{b}\left[\left(\prod_{t=0}^{T-1} \frac{\pi\left(A_{t} | S_{t}\right)}{b\left(A_{t} | S_{t}\right)} G_{0}\right)^2\right]\\&=\frac{1}{2}\cdot0.1\cdot((\frac{1}{0.5}))^2+\frac{1}{2}\cdot0.9\cdot\frac{1}{2}\cdot0.1\cdot((\frac{1}{0.5})^2)^2+...\\&=0.1\sum\limits_{k=0}^{\infty}0.9^k\cdot2^k\cdot2=\infty\end{aligned}$
3. 因此 $\operatorname{Var}[X] = \infty$。

7.增量实现

MC方法增量地实现，类似第二章中的方法。在第二章中，我们计算rewards的均值，而这里我们计算returns的均值，但是它们都是类似的。我们这里分别讨论ordinary和weighted两种情形。

ordinary
ordinary就是简单的计算均值，不过是把第二章中的 $R_i$替换为scaled returns就行了，也就是：

$Q_{n+1} = Q_n + \frac{1}{n} [\rho G_n - Q_n]$

weighted
对于weighted importance sampling，则必须进行一些修改，实际上也很简单。首先，我们观察下weighted importance sampling的公式：

$v_\pi(s) \doteq \frac {\sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1} G_t} {\sum_{t \in \mathcal{J}(s)} \rho_{t:T(t)-1}}$

我们把加权因子简写为 $W_k$，有：

$V_n \doteq \frac{\sum_{k=1}^{n-1} W_k G_k}{\sum_{k=1}^{n-1} W_k}$

分母是一个求和，我们用 $C_n=\sum_{i=1}^nW_i$记录。上式可以写为迭代的形式：

$V_{n+1} \doteq V_n + \frac{W_n}{C_n} [ G_n - V_n]$

$C_{n+1} = C_n + W_{n+1}$

proof:
$\begin{aligned} V_n + \frac{W_n}{C_n}[G_n - V_n] &= (1 - \frac{W_n}{C_n})V_n + \frac{W_n}{C_n}G_n \\ &= \frac{C_n - W_n}{C_n} \frac{\sum_{k=1}^{n-1} W_k G_k}{\sum_{k=1}^{n-1} W_k} + \frac{W_n G_n}{C_n} \\ &= \frac{C_{n-1}}{C_n}\frac{\sum_{k=1}^{n-1} W_k G_k}{C_{n-1}} + \frac{W_n G_n}{C_n} \\ &= \frac{\sum_{k-1}^n W_k G_k}{C_n}\\ & = V_{n+1} \end{aligned}$

注意 $C_0\doteq0$。这样，我们只需要记录当前的估值 $V_n$以及分母和 $C_n$即可。完整的off-policy的增量式MC策略评估算法如下：

对于on-policy方法，behavior policy与target policy一致，因此 $W\equiv1$。

8.off-policy的蒙特卡洛控制

off-policy是本书介绍的第二种control方法。off-policy中用于产生行为的策略叫做behavior policy，被改进的策略叫做target policy，这两者分开的好处是：即使target policy是确定性的，behavior policy仍然能采样所有actions，因此bebavior policy应该是soft的。

我们仍然基于GPI构造算法，以估计 $v*$或者 $q*$。其中target policy是关于当前估计值greedy的，而behavior policy我们一般选择 $\epsilon-soft$，即保证所有的状态-动作对能被visit无数次。

算法中标黄行的解释：因为 $\pi$是确定性策略，因此只有当 $\pi(S_t)=A_t$时，才是有意义的，一旦出现不等的情况，后面全部更新的权重都变成0了，于是不必再计算了。注意 $W$的更新分子是1，因为 $\pi$选择这个动作的概率是1。这也会导致learns only from the tails of episodes，可能降低学习速率，有时候会很严重。比较好的解决方法只能是TD了(下一章)，如果 $\gamma<1$，则TD也是最好的选择，因为到目前为止所介绍的重要性采样比率显然在 $\gamma<1$时不那么合理。

练习：Racetrack问题
小车从starting line出发，目标是finish line；分别考虑离散的水平和竖直速度，速度是一定范围内的离散量(+0~+4，上和右为正)；控制量为速度的增量(-1, -0, +1)；每个step得到-1的reward；冲出边界则回到起点速度清零，累积reward清0，但是episode不结束，该问题可用上面介绍的方法解决。

9.*Discounting-aware重要性采样

之前对off-policy的重要性采样权重都是把returns当作整体看的，没有考虑returns的内部结构，这里利用这个结构降低off-policy估计的方差，这在 $\gamma<1.0$时格外必要，因为此时重要性采样比率实际上不是很合理。

例如，考虑每个episode长100个steps， $\gamma=0$，则我们知道 $G_0=R_1$，而重要性采样却计算了后面所有动作选择概率的比值，而实际上只和第一个动作选择概率比值(factor)有关。后续的factor不改变期望更新，但是却极大地增加了方差(因为连乘的factor越多不确定性越大，方差越大)，有时甚至导致方差无穷大。

首先，我们引入部分累积回报(flat partial returns)的概念，h表示在第h步终结：

$\overline{G}_{t : h} \doteq R_{t+1}+R_{t+2}+\cdots+R_{h}, \quad 0 \leq t<h \leq T$

注意这里没有折扣因子，这就是flat的含义，partial表示不计算到终结，只计算到horizon h。我们用折扣因子 $\gamma$作为序列终止的概率，每一个step终止的概率为 $(1-\gamma)$，继续下一步的概率为 $\gamma$。因此第n步终结的概率为 $(1-\gamma)\cdot\gamma^{n-1}$。因此， $G_t$可以用flat partial returns来表示：

$\begin{aligned} G_{t} \doteq & R_{t+1}+\gamma R_{t+2}+\gamma^{2} R_{t+3}+\cdots+\gamma^{T-t-1} R_{T} \\=& (1-\gamma) R_{t+1} \\ &+(1-\gamma) \gamma\left(R_{t+1}+R_{t+2}\right) \\ &+(1-\gamma) \gamma^{2}\left(R_{t+1}+R_{t+2}+R_{t+3}\right) \\ & \vdots \\ &+(1-\gamma)\gamma^{T-t-2}\left(R_{t+1}+R_{t+2}+\cdots+R_{T}\right) \\ &+\gamma^{T-t-1}\left(R_{t+1}+R_{t+2}+\cdots+R_{T}\right) \\ &=(1-\gamma) \sum_{h=t+1}^{T-1} \gamma^{h-t-1} \overline{G}_{t:h}+\gamma^{T-t-1} \overline{G}_{t : T} \end{aligned}$

因为每一个 $\overline{G}_{t : h}$都是到h就终止了，因此我们只需乘重要性采样比率 $\rho_{t:h-1}$即可，我们分别写出ordinary情形与weighted情形：

ordinary: $V(s) \doteq \frac{\sum_{t \in J(s)}\left((1-\gamma) \sum_{h=t+1}^{T(t)-1} \gamma^{h-t-1} \rho_{t : h-1} \overline{G}_{t : h}+\gamma^{T(t)-t-1} \rho_{t : T(t)-1} \overline{G}_{t : T(t)}\right)}{|J(s)|}$

weighted: $V(s) \doteq \frac{\sum_{t \in J(s)}\left((1-\gamma) \sum_{h=t+1}^{T(t)-1} \gamma^{h-t-1} \rho_{t : h-1} \overline{G}_{t : h}+\gamma^{T(t)-t-1} \rho_{t : T(t)-1} \overline{G}_{t : T(t)}\right)}{\sum_{t \in J(s)}\left((1-\gamma) \sum_{h=t+1}^{T(t)-1} \gamma^{h-t-1} \rho_{t : h-1}+\gamma^{T(t)-t-1} \rho_{t : T(t)-1}\right)}$

这两种估计叫做discounting-aware重要性采样估计。当 $\gamma=1$时，其与标准的重要性采样一致。这不太容易写成增量的形式。weighted形式的分母是如何得到的还需要深入分析。

10.*Per-decision重要性采样

还有另外一种方式考虑off-policy重要性采样中return的结构，这种方式甚至可以减小 $\gamma=1$时的方差。首先我们变化下scaled returns：

$\begin{aligned} \rho_{t : T-1} G_{t} &=\rho_{t : T-1}\left(R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{T-t-1} R_{T}\right) \\ &=\rho_{t : T-1} R_{t+1}+\gamma \rho_{t : T-1} R_{t+2}+\cdots+\gamma^{T-t-1} \rho_{t : T-1} R_{T} \end{aligned}$

对这个式子中的第一项，我们继续展开：

$\rho_{t : T-1} R_{t+1}=\frac{\pi\left(A_{t} | S_{t}\right)}{b\left(A_{t} | S_{t}\right)} \frac{\pi\left(A_{t+1} | S_{t+1}\right)}{b\left(A_{t+1} | S_{t+1}\right)} \frac{\pi\left(A_{t+2} | S_{t+2}\right)}{b\left(A_{t+2} | S_{t+2}\right)} \cdots \frac{\pi\left(A_{T-1} | S_{T-1}\right)}{b\left(A_{T-1} | S_{T-1}\right)} R_{t+1}$

式子中只有一个reward: $R_{t+1}$，而该reward只与前面第一项因子: $\frac{\pi(A_t|S_t)}{b(A_t|S_t)}$有关，其它因子都是发生在 $R_{t+1}$之后的，因此我们得到：

$\begin{aligned}\mathbb{E}\left[\rho_{t : T-1} R_{t+1}\right]=& \mathbb{E}\left[\frac{\pi\left(A_{t+1} | S_{t+1}\right)}{b\left(A_{t+1} | S_{t+1}\right)} \frac{\pi\left(A_{t+2} | S_{t+2}\right)}{b\left(A_{t+2} | S_{t+2}\right)} \cdots \frac{\pi\left(A_{T-1} | S_{T-1}\right)}{b\left(A_{T-1} | S_{T-1}\right)}\right]\cdot\mathbb{E}\left[\frac{\pi(A_t|S_t)}{b(A_t|S_t)}R_{t+1}\right]\end{aligned}$

又因为:

$\mathbb{E}\left[\frac{\pi\left(A_{k} | S_{k}\right)}{b\left(A_{k} | S_{k}\right)}\right] \doteq \sum_{a} b\left(a | S_{k}\right) \frac{\pi\left(a | S_{k}\right)}{b\left(a | S_{k}\right)}=\sum_{a} \pi\left(a | S_{k}\right)=1$

因而有：
$\mathbb{E}\left[\rho_{t : T-1} R_{t+1}\right]=\mathbb{E}\left[\rho_{t : t} R_{t+1}\right]$

对于scaled returns展开式的其它项，也有这样的结论：

$\mathbb{E}\left[\rho_{t : T-1} R_{t+k}\right]=\mathbb{E}\left[\rho_{t : t+k-1} R_{t+k}\right]$

综合起来，我们得到：
$\mathbb{E}\left[\rho_{t : T-1} G_{t}\right]=\mathbb{E}\left[\tilde{G}_{t}\right]$
$\tilde{G}_{t}=\rho_{t : t} R_{t+1}+\gamma \rho_{t : t+1} R_{t+2}+\gamma^{2} \rho_{t : t+2} R_{t+3}+\cdots+\gamma^{T-t-1} \rho_{t : T-1} R_{T}$

我们把这个想法叫做per-decision重要性采样。然后我们可以得到ordinary类型的估计公式：

$V(s) \doteq \frac{\sum_{t \in \mathcal{T}(s)} \tilde{G}_{t}}{|J(s)|}$

对于first-visit情况，该方法是无偏的。

11.总结

MC直接从sample episodes中学习。MC相比于DP，有三个优势：可以直接从与环境的交互中学习最优行为，不需要模型；可以用在仿真或sample models中；可以高效地关注states的一个小子集，加速学习。此外，对不满足markov性的问题效果更好一些，因为不需要bootstrap。

MC是一种policy evaluation的方法，是无偏的，本章还讨论了episode-by-episode的基于MC的GPI，既可以是on-policy的，也可以是off-policy的，还可以增量实现。

MC的exploration性能不好，解决方法：每个episode从随机的state-action对开始，覆盖所有可能； 利用off-policy方法，可以用stocastic behavior学习确定的target policy。

off-policy预测是基于importance sampling的，包含ordinary importance sampling和weighted importance sampling，它们的特点：Ordinary importance sampling produces unbiased estimates, but has larger, possibly infinite, variance, whereas weighted importance sampling always has
finite variance and is preferred in practice。

• MC prediction.
• MC prediction of Action Values.
• MC Control.
• MCES - on policy.
• off policy MC, importance sampling.
• incremental implementation.
• discounting aware.
• per decision.

参考文献

1.https://zhuanlan.zhihu.com/c_1060499676423471104