这一篇来讲一下第四章,动态规划。
DP这个词,指的是一系列的算法,这些算法主要用来解决:当我有了一个可以完美模拟马尔可夫过程的模型之后,如何计算最优policies的问题。注意是policies,表明最优的策略可能不止一个。经典的DP算法在强化学习中的应用受限的原因有两个:一个是强假设满足不了,就是无法保证我能先有一个完美的模型来描述整个马尔可夫过程;另一个就是计算开销太大。但这仍掩盖不了其理论上的重要性。DP可以帮助我们更好地理解本书余下部分讨论的方法。事实上,这些方法都可以看成是尽可能的获得跟DP一样的效果,只是在强假设条件和计算开销上进行了优化。
从这章开始,我们假设我们面对的环境是有限MDP过程,也就是它的状态集合S和动作集合,都是有限的。其动态特性由一系列的状态转移矩阵给出:
当前reward的期望由下式给出:
尽管DP思想可以用于连续性的状态空间和动作空间,精确解只有在特定情形下才能得到。获得连续空间下的近似解的一种常用方法是把连续空间进行数值化变换,然后使用有限马尔可夫方法。我们第九章讨论的方法可以用于连续空间下的问题。
DP的核心思想,就是使用value function作为依据,指导policies的搜索过程。这一章我们讨论如何使用DP来计算第三章定义的value function。正如我们讨论过的,一旦我们找到了满足bellman 最优方程的最优value functions,我们就能找到最优policies。
回顾一下最优value function的定义:
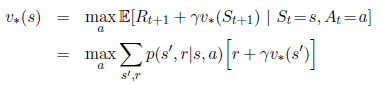
或者:
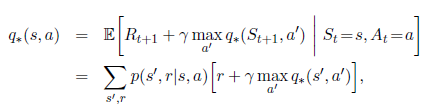
正如我们将要看到的那样,DP算法做的事情就是把这些bellman functions转变成优化value functions近似值的更新规则。
4.1 policy evaluation
首先我们来看一下如何计算对应任一policy的value function。这个叫做策略评估。我们也称之为prediction problem。回忆一下第三章,对于所有,

这里表示在policy为
,状态为s的情况下,action为a的概率。这个value function和上一段描述的并没有本质不同,只是多了policy的限制。只要满足
或者在策略
的情况下,所有的从状态s起始的路径都会有终止状态,那么这个valun function就是存在且唯一的。
如果环境的动态转移特性是完全可知的,那么上式其实就是个线性方程,带有
个未知数。在这种情况下,暴力解是可行的,也是是确定的。对于我们来说,迭代的计算方式是最适合的。假设我们有一系列的近似value function:
,每一个都把状态集合S映射到实数集R。最初的近似value function:
,是任意选择的(注意这里的0是指初始的value function,不是指状态的开始。事实上,每个迭代的value function都对所有的状态有个对应的实数映射。这也是为何后面会收敛于真实的
的原因)。然后后面的每一个近似value function都按照上式迭代求解。事实上,随着迭代的进行,最终value function会逐渐收敛于
。这个算法叫做iterative policy evaluation。
为了从得到后续的
,iterative policy evaluation针对每个状态s进行相同的操作如下:把当前状态s的value更新成一个新的value,这个新的value是由之后一个状态的旧的value和瞬时期望奖励,沿着所有可能的状态转移概率求和得到(仔细阅读上述公式)。我们把这个迭代操作叫做full backup。这个算法中的每一轮迭代操作都反向把所有状态的value值都推算(更新)一次,最后产生新的下一个
。DP中的反向操作都是full back up,因为每次操作都把所有可能的后续状态都涉及到了,而不是指采样某一个后续状态。
如果你想写一个描述iterative policy evaluation算法的程序,那么你应该由两个数组,其中一个保存,另一个保存
。这样的话,新的value就可以在不改变旧value值的情况下被一个个计算出来。当然只使用一个数组更容易,可以用“in place”的方式更新value。这种方式下,某个状态更新后的value就会实时的覆盖掉旧的value。由于不同状态的更新顺序不一样,有时候不能保证上述公式右边部分都用的是同一时刻某状态旧的value(可以这么理解:有时候恰好某个状态A的value更新较频繁,因为它与其他状态联系比较多,这样有可能下一次其他状态用到的A的value就是其更新两次或多次之后的)。这个稍微有些不同的算法同样最后收敛于
。事实上,它收敛的更快,因为每次只用某状态最新的value。对于这种“in place”的算法,状态被涉及到的顺序对收敛速度有着很大的影响。当我们考虑DP算法的时候,通常都考虑“in place”形式。伪代码如下:

虽然iterative policy evaluation算法最终肯定会收敛,但是实际程序中我们需要设置一个终止条件。一个典型的终止条件就是当的值非常小的时候,就让程序停止。
4.2 policy improvment
我们之所以要在某个policy下计算value function,是因为我们想要评估policy的好坏。假定我们已经确定了某一个policy下的value function 。那么对于一些状态s,我们想要进一步知道是不是可以改变一下policy来选择另外一个和当前policy的决定不一样的动作
。换句话说,我们已经知道当前的policy有多好了,那么改变成另一个policy是好一点呢还是坏一点呢?一个方法就是在当前s下选择你想选的a,然后继续按照已有的policy
走下去。这时的value迭代公式如下:

这里的关键点就在于上式和的大小比较。如果上式比
大,那么就是说当我在状态为s的时候选择a,然后继续按照policy
走下去,比我一直按照policy
走下去好,那么当我每次遇到状态s的时候,最好还是选择a。这样的一个policy就是一个好一点的new policy。
这时候一定会有人疑惑,刚才说的状态s,只是某一个状态,难道说在某一个状态下更好,就意味着真的更好?如果在其他的状态下反而不好怎么办?good question。这就是接下来要说的,policy improvment theorem。严格的数学的语言我就省略了,反正你只要知道,只要你发现在某个状态下有更好的选择a,那么保证其他选择都不变的情况下,这个新的policy一定在所有状态下都比前一个policy好!美妙啊!!我把证明贴上来,以防有人追根问底:

按照上述结论,我们考虑一下greedy policy :

greedy policy采取的动作是短期内最优的,但是这个短期指的是多看了一步。通过上式,可以看出greedy policy满足policy improvment theorem,因此,它一定比已有的policy更好或者至少一样好。这种通过构建greedy policy来得到更好的一个policy的方式,就叫做策略改进。
假设greedy policy和原有的policy一样好,也就是满足下式:
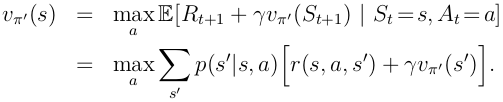
那么,这个方程看起来和bellman optimality value function是一模一样的,也就是说,原有的policy一定是最优policy。换句话说,policy improvment一定会给我们一个更好地policy,除非我们当前的policy已经是最优的了。
到目前为止,我们讨论的policy都是确定性的。在更广泛的意义上,policy是随机概率性的,比如。我们不去处理细节,但是这一节的思想可以无缝衔接到概率化的policy。
除此之外,如果有多个动作同时都可以得到相同的max value,那么在概率化的policy中我们不会去选其中之一,而是其中的每一个动作都会被以一定的概率选到。
4.3 policy iteration
一旦某个策略,经过policy improvement之后变成了一个更好地policy
,那么我们就能在此基础上进一步优化成更好的policy
,于是我们就能得到下图所示的更新序列:
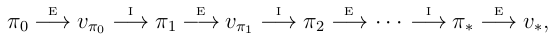
其中带有E的箭头表示policy evaluation,带有I的箭头表示policy improvement。每一个当前的policy,除非它已经是最优的,否则必然有一个better policy。由于有限马尔可夫过程的policy是有限的,那么这个过程一定会在有限的迭代次数后收敛于最优的policy。
上述这种找到最优policy的方法叫做policy iteration。下图给出了一个完整的算法。需要注意的是,上述序列的每一个policy evaluation 的过程,其本身也是一个iteration过程,以上一个policy的value function开始。这就加快了policy evaluation收敛的速度。
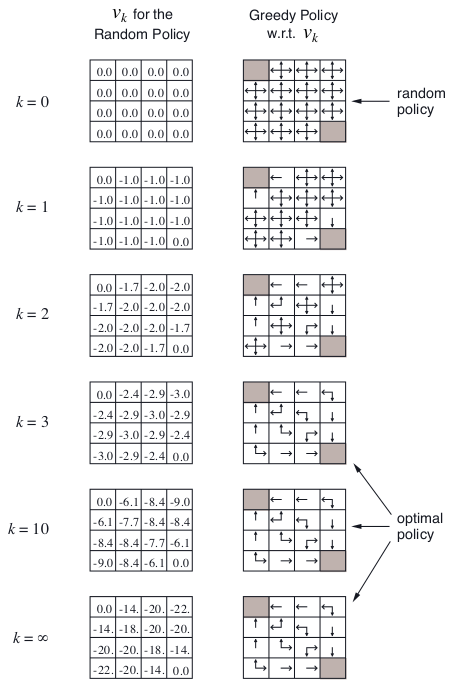
policy iteration经常会在有限的几个迭代后就收敛了。看一下下图的情形:左边的一列是随机策略下的value function在不同k下的evaluation过程;右边一列是对应每个k的value function结果的greedy policy。(这里要多说几句,以免误解了这个图的含义和上面的讲解:需要注意的是,如果按照前面policy evaluation的规则,应该是在收敛之后,才根据收敛的
确定一个greedy policy;而这里在k=1,k=2时都给出了相应的greedy policy,是为了后面的value iteration做铺垫,为了告诉读者,有时不需要等到
彻底收敛才确定greedy policy)
下面给出完整的policy iteration的算法伪代码:

这份伪代码里面有个小bug,就是当最终policy收敛于最优的时候,可能不会停止迭代,而是不断的在几个最优的policy之间来回跳跃。
4.4 value iteration
policy iteration算法的一个缺点是其迭代过程每次都包含一次policy evaluation,而这个policy evalution过程本身就是一遍遍的迭代。当然,等到policy evaluation彻底结束是好的,因为可以保证精确地收敛到
。然而我们必须要这个精确的收敛吗?我们能不能在中间就停止evaluation过程以加快收敛速度呢?上面给出的那个图就告诉我们,有时候提前终止evaluation过程其实也能得到最优policy。
事实上,上面的猜想是肯定的,的确可以通过某些方式来缩短evaluation的过程,同时又不会损失收敛性。其中一个特别的方式就是当所有状态都遍历一遍后,停止evaluation过程。这个算法就叫做value iteration。公式如下:
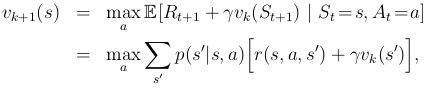
另外一个理解value iteration的方式是参考贝尔曼最优方程。我们注意到value iteration本质上是简单地把贝尔曼最优方程转化成一个更新规则。同意注意到value iteration的backup过程和之前的policy evaluation的backup过程是一模一样的,只是在value iteration过程中每次我们都需要所有动作中获得上式最大值的那个。
最后,我们需要考虑一下value iteration如何终止。和policy evaluation相同,我们理论上需要无限次迭代使收敛到
。在实际应用中,我们在相邻两次遍历状态的
的差值非常小时,就停止运行。
我们可以看出,value iteration高效地结合了policy evaluation和policy improvement,这样就获得了更快的收敛速度。总体来讲,这一大类的policy iteration算法都可以看作是一系列的遍历序列,一部分遍历序列使用了policy evaluation的backup,另一部分使用了value iteration的backup。因为仅有的不同之处只是上式中的max操作,因为我们可以认为是把一些max操作加入了policy evaluation过程。所有这些算法对于discounted finite MDP来说都会收敛到最优policy。
4.5 Asynchronous Dynamic Programming
到目前为止,我们讨论的DP算法的一个较大的缺陷是我们必须使用整个状态集。如果状态集数量非常大,那么就算是单次遍历也非常耗时。
非同步DP算法是这样一类实时迭代式DP算法:它不要求规范系统的遍历顺序。它们可以按照任意顺序进行反向计算过程,而不管当时计算时遇到的状态价值是不是同步更新的。为了使得收敛准确性不受影响,非同步DP算法必须要遍历过所有的状态价值:它不能在计算过程中刻意忽略一些状态。非同步DP算法带来了很大的灵活性,使得我们可以去选择使用哪些状态做反向计算。
比如:有某个非同步value iteration算法在每一步只是反向更新一个状态。如果
,那么当且仅当所有的状态在{
}序列中出现无穷多次,最终的价值函数才能收敛于
。尽管这些不太常见的非同步DP算法的细节讨论超出了本书的范围,我们依然可以很清晰的看出一些特别的backup方式使得很多非遍历形式的DP算法变得更加灵活。
诚然,尽可能地避免遍历过程并非意味着我们可以有很少的计算量。它只是意味着我们可以适当的逃离一些毫无意义的遍历过程。我们可以利用这种灵活性去选择那些真正能让算法效率更高的状态价值去遍历。我们甚至可以直接跳过那些对实际最优行为无关的状态不去遍历。第8章讨论了这类问题。
非同步DP同时也使得我们可以在实时的交互过程中加入计算过程。为了解决一个MDP问题,我们可以在执行机构与环境交互作用的同时,运行之前讨论的那些迭代式DP算法。agent的经验可以帮助决定哪些状态需要反向计算;同时,最新的价值函数和policy信息也可以帮助agent来做出决策。这样可以让DP算法的反向计算过程集中于那些真正和agent相关的状态。这种局部集中的思想在强化学习中被再三强调。
4.6 Generalized Policy Iteration
policy iteration包含两个即同时发生,又相互影响的过程。其中一个过程使value function和当前的policy保持一致(policy evaluation),而另一个过程依据当前的value function给出greedy policy。在policy iteration中,这两个子过程交替进行,但是并非真的必要。比如在value iteration中,两次policy improvement之间只有一次evaluation的迭代过程。在非同步DP方法中,上述两个子过程的交错更加精细:在有些情况下,一个过程中仅有一个状态被更新。其实只要能保证所有状态都能被持续遍历,其具体顺序是不太重要的,因为最终的结果都是一样的--收敛于最优value function和最优policy。
我们用一个名词“generalized policy iteration”(GPI)来表征广泛意义上的上述两个子过程,而不去过分关注细节。几乎所有的强化学习方法都可以用GPI来很好的表述。也就是说,所有这些方法都有相似的内涵:policy永远是根据value function来进行improvement过程;而value function一直被驱使成为当前policy下的最优value function。下图可以很清楚地描述这种相互过程:
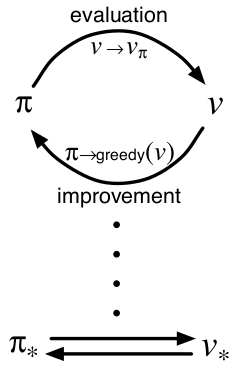
很容易看出如果improvement和evaluation过程都基本稳定下来了,也就是不再有很大的变化,那么当前的value function和policy一定是最优的。这种情况也是贝尔曼最优方程成立的情形,因此value function和policy一定同时是最优的。
GPI中的evaluation和improvement过程可以说是既相互竞争,又在相互协作。说它们相互竞争意思是这个过程在向着相反的方向走:根据当前的value function把policy变成greedy形式,其实就是否定了当前value function相对于改变后的greedy policy的正确性;而对value function进行更新使之和当前policy相一致,也就意味着当前的policy对于更新后的value function来说,不再greedy。在长期交互作用中,这两个子过程却可以找到同一个最终答案:最优的policy和最优的value function。
我们也可以如下图这样考虑:
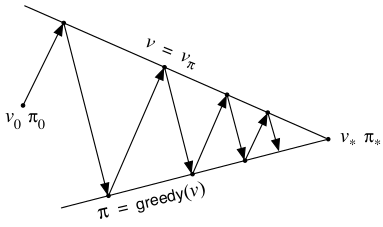
尽管真实的情形比这个图要复杂,但是该图的确反映了一些抽象的内在含义。每个子过程(指的是improvement和evaluation其中之一)都在驱使value function或者policy向着两个目标其中之一前进(两个目标指的是上下两条成角度的线)。尽管向着其中一个目标前进必然离另一个目标远一些,但是因为最终两条线有共同的交点,也就是最终会达到唯一的solution:optimal value function和optimal policy。
4.7 Efficiency of Dynamic Programming
DP算法对于规模非常大的问题也许不太适用,但是相比其他解决MDP问题的方法,已经高效很多。如果我们忽略一些技术细节,其实DP算法的worst case时间复杂度是基于状态集个动作集数量之和的多项式复杂度。就算所有policies的总数是,DP算法也总能保证在多项式复杂度的时间内找到最优解。在这个层面上,DP比直接对policies集合进行搜索快指数倍,因为直接搜索需要详尽地检查每一个policy。线性规划方法也可以用于解决MDP问题,并且在一些情况下其worst-case的收敛速度要好于DP。但是在很多小规模的问题中,线性规划表现的并不好。对于超大型的问题,只有DP是可行的。
DP有时被认为会受限于“维度灾难”的问题而不能得到广泛运用,也就是随着状态变量的增多,状态数量会成指数倍的飙升。过大的状态集的确带来困难,但那是问题内在的困难,并非DP的困难。事实上,DP对于大型问题的效果要比暴力搜索和线性规划强的多。
实际应用中,使用现代计算机,DP可以完成百万级别状态数的MDP问题的解决。policy iteration和value iteration方法都用的很广泛,很难说哪一种更好。实际中,这些方法的收敛速度比它们理论上的worst case的收敛速度都要快的多,尤其是当初始value function或者policy的设置很恰当的时候。
对于超大型规模的状态集,非同步DP算法更加受到追捧。对于同步DP算法来说,当连单次状态集的遍历也变得不可行的时候,问题依旧可以解决。其实,并非所有的状态对于最优解都是必须的。这时候非同步DP算法就可以站出来解决这类问题,往往会得到比同步DP算法更快更好的结果。
4.8 Summary
这一章我们熟悉了用以解决MDP类问题的动态规划算法的基本概念。Policy evaluation指的是按照给定policy进行value function的迭代计算;policy improvement指的是按照当前的value function进行policy的改进。把这两部分合并在一个过程里,我们得到了policy iteration和value iteration。它俩之中任何一个都可以高效解决finite MDP问题。
经典DP算法对整个状态集进行遍历,对每一个状态进行“反向更新”(full backup)计算。每一次backup依据所有可能的后续状态和转移概率来更新状态的value。Full backup过程和贝尔曼方程很像:只不过是把贝尔曼方程转化成了赋值规则。当backup计算不再变化时,说明这个时候的values已经收敛到可以满足贝尔曼方程了。为了直观看出backup过程,我们可以使用backup diagram(上文给出了)。
深入分析DP算法或者所有的强化学习算法的本质,我们可以把他们都看作是GPI(generalized policy iteration)。GPI包含两个互相作用的子过程:其中一个根据给定的policy改变value function,使value function给符合当下的policy;另一个根据value function改变policy,使policy更好。这俩过程看起来是在拆对方的台,但事实上最终会得到最优的结果。在一些情况下,GPI可被证明收敛,另一些情况下,虽然GPI不一定收敛,但是仍帮助我们理解这类方法的内涵。
有时并不一定非得遍历所有状态:非同步DP就是这种以任意顺序遍历状态的方法,甚至是随机遍历或者使用过时的value信息。
最后,我们注意到DP算法的最后一个重要性质:它们都在其他estimates的基础上更新某个estimates。我们把这种思想叫做:bootstrapping(所谓的Bootstrapping法就是利用有限的样本资料经由多次重复抽样,重新建立起足以代表母体样本分布之新样本)。下一章我们会讨论既不需要model也不需要bootstrapping的算法。再下一章我们讨论不需要model但是需要bootstrapping的方法