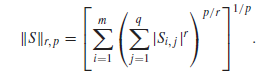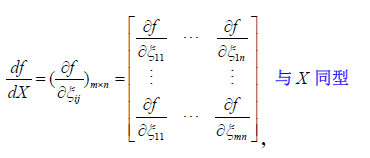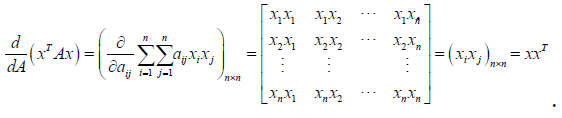常用的矩阵范数和矩阵导数

1.常用的矩阵范数

矩阵的 $l_{r,p}$范数定义为：

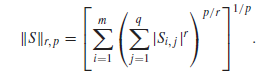
F范数和 $l_{2,1}$范数可以转化为：

$S$的 $l_{2,1}$范数其实就是每一行向量的 $l_2$范数之和。在最小化问题中，只有每一行的 $l_2$范数最小才能使总和最小，而每一个行范数最小就要求行内尽可能多的元素为0，即行稀疏。所以，通过约束矩阵的 $l_{2,1}$范数会得到一个行稀疏的矩阵。

矩阵 $S$的 $l_2$范数是所有元素的平方和再开方， $l_2$范数可以防止过拟合，提升模型的泛化能力。 $l_2$范数最小，会使矩阵中的每一个元素都很小，接近于0。与 $l_1$范数不同， $l_2$范数不会让元素等于0，而是接近0.

核范数为矩阵奇异值的和，用于约束低秩。因为 $rank(W)$是非凸的，故在优化中常使用其凸近似，也就是核范数。

2.标量函数对矩阵变量求导

定义：矩阵X，函数f(X)是以X为自变量的数量函数，定义f(X)对X的导数为

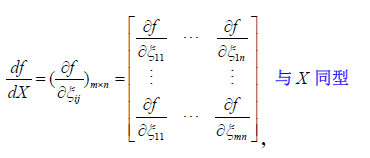
例如：

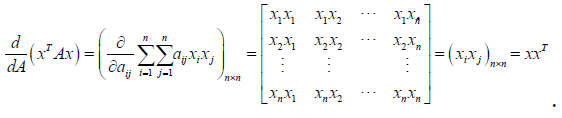
常用的矩阵导数有：

$\frac{\partial tr(Q^{T}AQ)}{\partial Q}=(A+A^{T})Q$

$\frac{\partial tr(QAQ^{T})}{\partial Q}=Q(A+A^{T})$

$\frac{\partial tr(AB)}{\partial A}=\frac{\partial tr(BA)}{\partial A}=B^{T}$

$\frac{\partial tr(AA^T)}{\partial A}=2A$ , $\frac{\partial tr(A^2)}{\partial A}=2A^T$

$\frac{\partial tr(Q^{T}A)}{\partial Q}=\frac{\partial tr(A^{T}Q)}{\partial Q}=\frac{\partial tr(AQ^{T})}{\partial Q}=A$

$tr(ABC)=tr(CAB)=tr(BCA)$