范数丨向量范数和矩阵范数

范数

​   有时我们需要衡量一个向量的大小。在机器学习中，我们经常使用被称为范数$（norm）$的函数衡量向量大小。形式上，$L^P$范数定义如下：

$$||x||_p=(\sum_{i}{|x_i|^p})^{\frac{1}{p}}$$
​   其中 $p \in R,p \geq 1$。

​   范数（包括$L^P$范数）是将向量映射到非负值函数。直观上来说，向量$x$的范数是衡量从原点到点$x$的距离。更严格地说，范数是满足下列性质的任意函数：

• $f(x) = 0 ⇒ x = 0$
• $f(x + y) ≤ f(x) + f(y) （三角不等式 (triangle \space inequality)）$
• $∀α ∈ R, f(αx) = |α|f(x)$

向量范数

$L^0$范数

  有时候我们会统计向量中非零元素的个数来衡量向量的大小。有些作者将这种函数称为 “$L^0$范数’’，但是这个术语在数学意义上是不对的。向量的非零元素的数目不是范数，因为对标量放缩 $α$倍不会改变该向量非零的数目。因此，$L^1$ 范数经常作为表示非零元素数目的替代函数。

$L^1$范数

  $L^1$范数是我们经常见到的一种范数，它的定义如下：

$$||x||_1=\sum_{i}{|x_i|}$$
  表示向量 $x$中非零元素的绝对值之和。 matlab函数如下：

norm(x,1);

$L^2$范数

  $L^2$范数是我们最常见最常用的范数了，我们用的最多的度量距离欧氏距离就是一种$L^2$范数，它的定义如下：

$$||x||_2=\sqrt{\sum_ix_i^2}$$
  Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方。 matlab函数如下：

norm(x,2);

$L^{\infty}$范数

$$||x||_{\infty}=\max_{i}|x_i|$$

  即所有向量元素绝对值中的最大值，matlab调用函数:

norm(x,inf);

$L^{-\infty}$范数

$$||x||_{-\infty}=\min_i|x_i|$$

  即所有向量元素绝对值中的最小值，matlab调用函数:

norm(x,-inf);

$L^{p}$范数

$$L_p=\sqrt[p]{\sum\limits_{1}^n x_i^p}，x=(x_1,x_2,\cdots,x_n)$$

  即向量元素绝对值的p次方和的1/p次幂，matlab调用函数:

norm(x, p);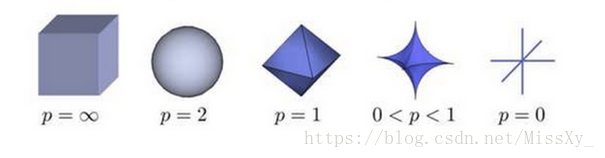

  上图表示了p从无穷到0变化时，三维空间中到原点的距离（范数）为1的点构成的图形的变化情况。以常见的$L^2$范数$（p=2）$为例，此时的范数也即欧氏距离，空间中到原点的欧氏距离为1的点构成了一个球面。

矩阵范数

$L^1$范数

$$||A||_1=\max_j\sum_{i=1}^{m}|a_{i,j}|$$

  列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数:

norm(A, 1);

$L^2$范数

$$||A||_2=\sqrt{\lambda_1}$$

  其中$\lambda \in A^TA$的最大特征值。

  谱范数，即$A^TA$矩阵的最大特征值的开平方。matlab调用函数：

norm(A, 2);

$L^\infty$范数

$$||A||_\infty=\max_i\sum_{j=1}^{N}|a_{i,j}|$$

  行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数：

norm(A, inf);

$L^F$范数

$$||L||_F=(\sum_{i=1}^{m}\sum_{j=1}^{n}|a_{i,j}|^2)^\frac{1}{2}$$

  Frobenius 范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数：

norm(A,'fro');

$L^*$核范数

$$||A||_*=\sum_{i=1}^{n}\lambda_i$$

  其中,$\lambda_i$是$A$的奇异值。

  所以核范数是奇异值之和。