向量和矩阵的范数整理

范数（norm）

范数是数学中的一个基本概念，它常常用来度量某个向量空间（或矩阵）中的每个向量的长度或者大小，以此来进行比较。

向量的范数

对向量的范数先进行一个直观的认识。此处引用知乎作者Faaany所举的例子：

在一维的实数集合中，我们随便指出两个数字，如4和9，就很容易可以得到9>4。但是当到了二维实数空间中，如（1，1）和（0，3）就没有办法进行比较了。但是如果引入了范数这个概念，我们就可以将（1，1）和（0，3）作为两个向量，通过范数映射。

到实数 $\sqrt{2}$ 和3，这样我们就可以进行比较了。所以这时可以看出，范数作为了一个函数，它将不能进行比较的向量转换为了可以比较的实数。

下面介绍向量的几种常用的范数：

1-范数

即向量中所有元素的绝对值之和。

$\left \| x \right \|_{1}=\sum_{i=1}^{n}\left | x_{i} \right |$

2-范数

即向量中每个元素的平方和再开平方根，即欧氏距离。

$\left \| x \right \|_{2}=(\sum_{i=1}^{n} x_{i}^{2})^{\frac{1}{2}}$

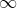$\infty$ -范数

即所有向量元素中的最大值。

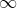$\left \| x \right \|_{\infty }=max \left ( \left | x_{i} \right |\right )$

- $\infty$ -范数

即所有向量元素中的最小值。

$\left \| x \right \|_{-\infty }=min \left ( \left | x_{i} \right |\right )$

p-范数

即所有向量元素的p次方之和的1/p次幂。

$\left \| x \right \|_{p}=(\sum_{i=1}^{n}\left | x_{i} \right |^{p})^{\frac{1}{p}}$

最后以知乎作者黄大宁cn举的例子加深对向量的范数的印象：

“

佟湘玉有一天在同福客栈说：“额滴神呐，展堂，你说隔壁的赛貂蝉有什么好。”老白：“她没你温柔，没你贤惠，没你大气，没你端庄。”佟湘玉：“那为啥你们总往她那跑呢?”老白：“因为他的相貌是满分啊”。

”

看到没有？如果用二范数来衡量赛貂蝉和佟湘玉，那么可以说佟湘玉并不占下风，但是压不住人家赛貂蝉有一个满分啊，也就是说，从无穷范数的角度来看，赛貂蝉的稳稳超过佟湘玉的。

矩阵的范数

假设矩阵的大小为m×n，即m行n列。再举个例子:

$A=\begin{bmatrix} 1 &2 &3 \\ -4&5 &-6 \end{bmatrix}$

1-范数

也称列和范数。即矩阵列向量中绝对值之和的最大值。

$\left \| A \right \|_{1}=max(\sum_{i=1}^{m}\left | a_{ij} \right |)$

先计算每列的绝对值之和就可以得到[5 7 9]，然后取最大值就是9。

2-范数

又称谱范数，计算方法是 $A^{T}A$ 矩阵的最大特征值的平方根。

$\left \| A \right \|_{2}=\sqrt{\lambda_{1}}$

其中， $\lambda _{1}$ 是 $A^{T}A$ 的最大特征值。

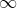$\infty$ -范数

又称行和范数。即矩阵行向量中绝对值之和的最大值。

$\left \| A \right \|_{\infty }=max(\sum_{j=1}^{m}\left | a_{ij} \right |)$

则上面的例子得到的就是[6, 16]，在取最大值就是16。

F-范数

Frobenius范数，计算方法就是矩阵中各个元素的绝对值的平方和在开方。

$\left \| A \right \|_{F}=(\sum_{i=1}^{m}\sum_{j=1}^{n}\left | a_{ij} \right |^{2})^{\frac{1}{2}}$

ref:https://blog.csdn.net/bitcarmanlee/article/details/51945271