Noise2noise: Learning image restoration without clean data
Paper:https://arxiv.org/abs/1803.04189
Code:https://github.com/NVlabs/noise2noise
1.Main idea
It is possible to learn to restore images by only looking at corrupted examples (without clean data).
Learn to turn bad images into good images by only looking at bad images.
2.Understanding
2.1 Loss function
Propaedeutics of loss function:
http://www.chioka.in/differences-between-l1-and-l2-as-loss-function-and-regularization/
http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/
Example in paper:

L1 loss is the median(中值)
L2 loss is the mean(均值)
L0 loss is the mode (众数)
But why?
http://www.johnmyleswhite.com/notebook/2013/03/22/modes-medians-and-means-an-unifying-perspective/
https://stats.stackexchange.com/questions/34613/l1-regression-estimates-median-whereas-l2-regression-estimates-mean

对L1损失和L2损失这个多元函数求偏导,我们关注的是
这个变量,偏导为0,即此时可以理解为损失取到最小值。上述公式已经很易理解了。
L1损失求偏导后,
已经被当成常量,即因绝对值符号,求和符号内部的值只能为正负1(即用符号函数
表示),得保证
的值大于和小于
的数量尽可能相等,才能抵消为0,所以为中值。
L2损失求偏导后,按照公式,很明显的,当其等于0的时候,
应等于所有
的均值。
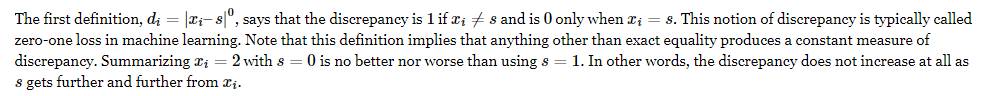
2.2 Problem form transformation

2.3 Challenges and opportunities

模型在使用L2损失的时候,具有输出对应样本标签的均值的趋势(见上2.1节解释),所以可能会造成一定程度的模糊(平滑)。但是却有意想不到的优势。
不论怎么改变我们的标签目标数据(在标签数据匹配对应期望的前提下),使用L2损失训练模型的最终输出结果仍然不会改变。
因此,如果用具有相同条件期望值的任意分布代替输入条件下的目标分布
,模型最优网络参数
仍然不变。


所以,当目标标签被加上0均值的噪声后,在不改变网络的前提下,模型仍然能够实现恢复。
当数据量趋于无限多的时候,(6)式就如同(1)式了,和一般的标签对使经验误差最小的结果一样。因为求得的结果总是这一系列数据标签的均值,但该数据标签并不是真的的标签,所以在数据量增大后,保证期望不变的前提下,那么结果很明显的最后就是非常接近真值。
当数据量有限的情况下,那么即存在一定误差。其中真实标签
和受损的标签
的期望平方差如下:
其中有:
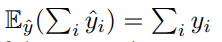
PS:此时受损标签的数据量为N,其均值仍然为
。
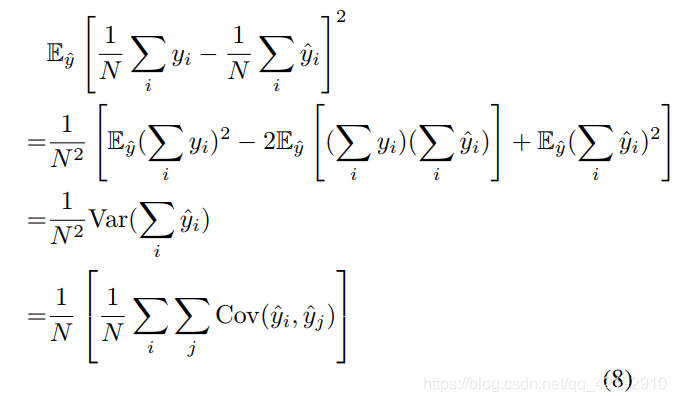
其实按照上述推算,平方打开后的结果应该是0的,但是为什么却不是呢?因为我们的数据标签始终是有限的,它只能是每一次图像处理保证均值不变,但是所有的样本数据的均值却可能会出现偏差,所以结果如下式:
(此时可以注意到了,当数据无限的时候,那么所有样本的均值就不会出现偏差了!)
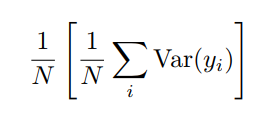
此时用了方差来表示了。所以随着样本数N的增加,偏差会越来越小,即使是有限的数据,也能接近做到无偏差。
2.4 Others
由于L1损失恢复的是中值,所以该方法同样可以去除显著异常的内容,在paper中给出的例子是去除文字。

在测试中,当大量像素随机后,发现L2和L1损失来训练模型的效果均出现一定问题:
L2损失的结果会使图像的恢复结果向某一个颜色偏向。(可参考2.1节的链接)
L1损失的结果是中值,所以大量像素的偏离也无法恢复。

使用到了退火版的L0损失展现出了优秀的结果。因为正确的像素仍然没有改变,即使它只占据了10%左右,其出现的次数仍然是占据大多数的。L0损失使像素向正确方向众数进行了偏移。(mode seeking 众数寻求)

But why?
在2.1节已经解释出L0损失是众数,但在paper中,解释如下:
实际上,恢复结果应该是在损失函数导数为0的点,L0范数的最小化理应是众数,但实验中恢复的却是希尔伯特变换的0点。在各种数值实验中验证了这种行为,并在实践中发现,估计值通常接近真实结果的众数。
(其实结果值还是接近的是众数,但是却只证明到了其是希尔伯特变换的0点,并不是损失函数导数的0点)
这可以通过希尔伯特变换近似微分(用符号翻转)来解释。
通过希尔伯特变换后,值为0才能找到最值。所以原始信号为
,冲激响应为
,通过傅里叶变换即有乘以
(时域相卷,频域相乘)(
为
的频域转换)
但是直接的傅里叶变换却是乘以
。
可以理解为近似的。(此处还存在疑问)
参考:
https://blog.csdn.net/yrlgg/article/details/79595859
https://www.cnblogs.com/husi253/p/4609505.html
https://blog.csdn.net/edogawachia/article/details/79366444

(10)式除以了p,适当的归一化,且忽略了范数的p次根号,然后根据
密度函数进行积分。
(11)式进行偏导处理(对x求偏导,把y看作常量),等于0时,得到最小值。
注意到,实际上并没有0范数,范数要求
,但此时
趋近于0也是成立的。(此时可以发现
取0,1,2都有其对应的意思,即是L0,L1,L2)。也对应了2.1节。
(12)式即是
的希尔伯特变换,该式为0即找到最值。
(其中 up to a constant multiplier 还存在疑问)

注意:此时并没有像2.1节解释L1和L2损失用的是离散,此时用的是连续的随机变量,那么就不是求和而是积分。
作者对不同噪声设计的损失函数具有很大的开拓性。
High dynamic range (HDR) loss:
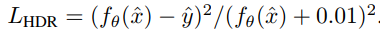
MRI:核磁共振图像的损失函数:
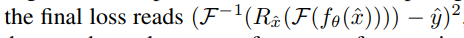
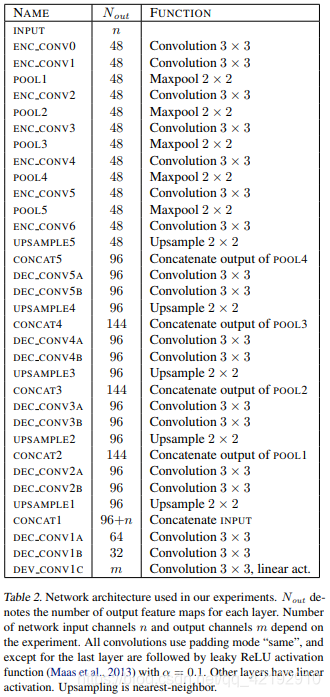
3.Architecture
U-net