前言
笔记和图片整理来自于知乎 马同学
相似矩阵
同一个线性变换,在不同基下的矩阵,称为相似矩阵。
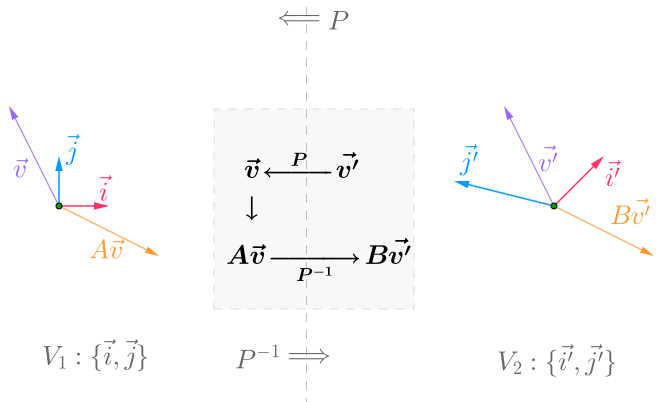
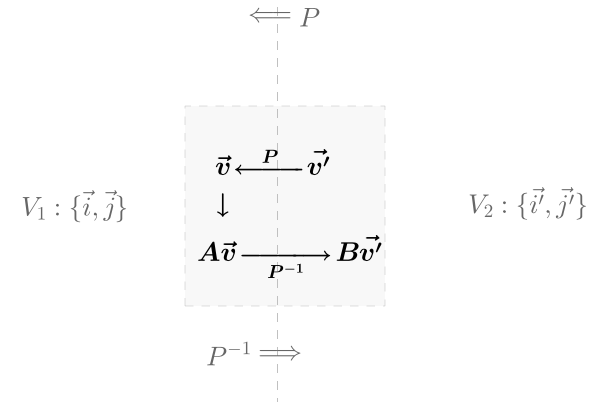
解释:
- \(\vec{v'}\) 是 V2 下的点
- \(\vec{v'}\) 通过 P 变为 V1 下的点,即 \(P\vec{v'}\)
- 在 V1 下,通过 A 矩阵完成线性变换,即 \(AP\vec{v'}\)
- 通过 \(P^{-1}\) 从变回 V2 下的点,即 \(P^{-1}AP\vec{v'}\)
综上,我们可以有:
\(B\vec{v'}=P^{-1}AP\vec{v'}\)
我们可以认为:
\(B=P^{-1}AP\)
那么 B 和 A 互为相似矩阵。
那么P呢?
首先我们给出空间中的一点,比如说 m 点吧:
相信大家可以理解,不论有没有基,这个点都是客观存在的。
然后,我们给出 m 点在 \(\vec{i'},\vec{j'}\) 的坐标 \(\vec{v'}\) :
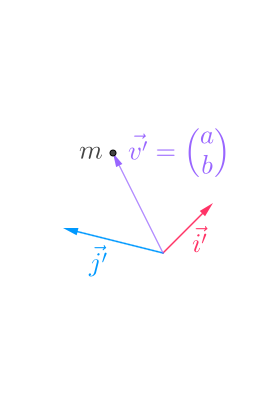
为了表示 \(\vec{v'}\)是 \(\vec{i'},\vec{j'}\) 下的坐标,我们写成这样:
\(\vec{v'}=\begin{pmatrix} a b\end{pmatrix}=a\vec{i'}+b\vec{j'}\)
如果我们知道了 \(\vec{i'},\vec{j'}\) 在 \(\vec{i},\vec{j}\) 下的坐标:
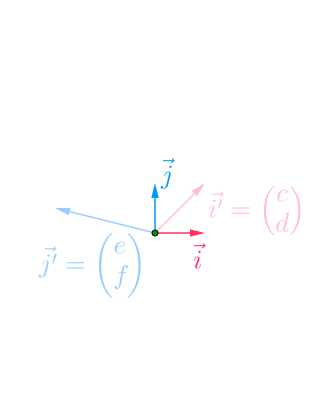
那么有:
此时,实际上 m 点的坐标,已经变到了$ \vec{i},\vec{j}$ 下的 \(\vec{v}\) :
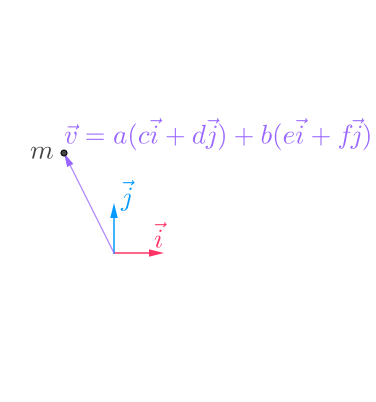
坐标已经转换了,继续往下推:
P 其实就是:
\(P=\begin{pmatrix} \vec{i'} & \vec{j'} \end{pmatrix}\)
要记得啊,上面的 \(\vec{i'},\vec{j'}\) 是在 \(\vec{i},\vec{j}\) 下的坐标。