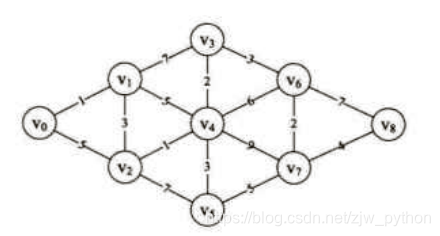
1 测试图建立(邻接矩阵)
class Graph{
constructor(v,vr){
let len = v.length
this.vexs = [].slice.apply(v);
let arcs = [];
for (let i=0;i<len;i++){
arcs[i] = new Array(len);
for (let j=0;j<len;j++){
arcs[i][j] = i===j ? 0 : 65535;
}
}
for (let arc of vr){
let v1 = v.indexOf(arc[0]);
let v2 = v.indexOf(arc[1]);
arcs[v1][v2] = arcs[v2][v1] = arc[2] || 1;
}
this.arcs = arcs;
}
}
let a = new Graph(['v0','v1','v2','v3','v4','v5','v6','v7','v8'],[['v0','v1',1],['v0','v2',5],['v1','v3',7],['v1','v4',5],['v1','v2',3],['v2','v4',1],['v2','v5',7],['v3','v6',3],['v4','v6',6],['v4','v7',9],['v5','v7',5],['v6','v8',7],['v7','v8',4],['v6','v7',2],['v3','v4',2],['v4','v5',3]]);
console.log(a);
2 Dijkstra算法
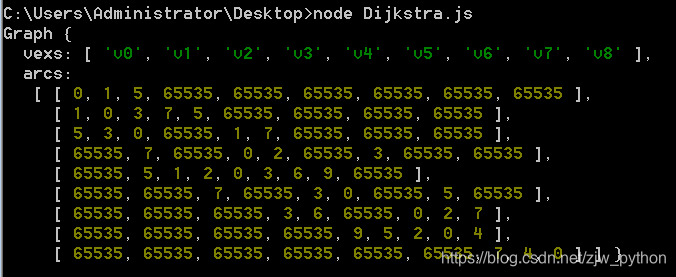
迪杰斯特拉(Dijkstra)算法是一个按路径长度递增的次序产生最短路径的算法。当计算图中顶点v0至图中另一顶点vn的最短路径时,其算法思路是先将v0与各顶点的距离放入一个数组A,然后找到离v0距离最近的顶点v1,然后更新数组A,比较顶点v0至顶点v1距离加上顶点v1至所有顶点距离和与原本数组对应值的大小,若距离更小,则替换之。接着寻找下一个离v0最近的顶点v2,然后重复以上过程,最终数组A就保存着顶点v0到图中所有顶点的最短距离。
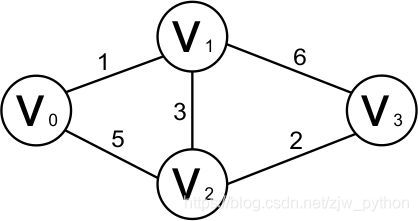
如下图,计算顶点v0至顶点v3的最短路径
首先初始化数组A,存储放v0与各顶点的距离,此时数组为:
| 0 | 1 | 5 | 65535 |
|---|
可以得知,顶点v1距离v0最近,因此比较顶点v1至所有顶点的距离,更新数组A,发现v0-v1-v2的距离比v0-v2更短,替换后,数组A如下:
| 0 | 1 | 4 | 7 |
|---|
寻找下一个离v0距离最近的顶点,即v2,重复以上过程,更新数组为:
| 0 | 1 | 4 | 6 |
|---|
找到最后一个顶点v3,所有顶点已经遍历完成,得出顶点v0至v3的最短路径值为6
完整的算法如下:
function Dijkstra(G,v0){
let shortPath = new Array(G.vexs.length); //用于存储顶点v0到各顶点的路径值
let path = new Array(G.vexs.length); //用于储存顶点v0到各顶点的路径
let visited = new Array(G.vexs.length); //用于指示图中的顶点是否访问过
for (let i=0;i<G.vexs.length;i++){
shortPath[i] = G.arcs[v0][i]; //初始化为顶点v0到各顶点的边权值
path[i] = 0; //初始化为0
visited[i] = false; //初始化未访问过
}
var mini,closestVex; //用于记录当前最近的节点距离值和节点序号
shortPath[v0] = 0; //v0到自身的距离为0
visited[v0] = true; //v0自身已经访问过
for (let i=1;i<G.vexs.length;i++){ //遍历其余顶点
mini = 65535; //初始距离值为无穷
closestVex = v0;
for (let j=0;j<G.vexs.length;j++){ //寻找当前未访问过且离v0最近的节点
if (!visited[j] && shortPath[j] < mini){
mini = shortPath[j];
closestVex = j;
}
}
visited[closestVex] = true; //将当前离v0最近的节点设置为已访问
for (let j=0;j<G.vexs.length;j++){ //更新距离数组
if (!visited[j] && mini+G.arcs[closestVex][j] < shortPath[j]){
shortPath[j] = mini+G.arcs[closestVex][j]; //替换为更近的距离值
path[j] = closestVex; //记录节点序号
}
}
}
console.log(shortPath);
console.log(path);
}
Dijkstra(a,0);
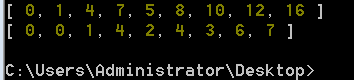
结果如下图所示,第一个数组中表示顶点v0到各顶点的最短距离值,而第二个数组则为路径,例如查询v0到v8的路径,则从数组第8个元素开始向前追溯,为8-7-6-3-4-2-1-0
从循环嵌套可以看出,此算法的时间复杂度为O(n2)
3 Floyd算法
Floyd算法是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法。假设求从顶点vi到vj的最短路径,那么不包含头尾顶点,该路径最多可路过了k个顶点( k = n-2,n为图的顶点数),对于第k个顶点,最短路径是否经过该节点取决于起点vi到第k个节点的最短路径加上第k个节点到终点vj的路径长度和与不经过第k个节点的最短路径长度的大小关系,即(vi, vk)+ (vk, vj)与(vi, vj)的路径长度,而要知道这两者谁大谁小,那么又必须知道起点vi到节点vk的最短路径,此最短路径又与起点到第k-1节点的最短路径加上第k-1个节点到第k个节点的路径长度和与不经过第k-1个节点至第k个节点的路径长度的大小关系有关,即(vi, vk-1)+ (vk-1, vk)与(vi, vk),依次类推。
该算法从最初的邻接矩阵D开始,遍历每个节点,对于当前节点k,若存在D(v,w) > D(v,k)+ D(k,w),那么就将D(v,w)值替换为D(v,k)+ D(k,w),这样一步一步替换每个节点,最终得出图中所有顶点到所有顶点的最短路径。
function Floyd(G){
let D = []; //用于存储图中所有顶点到所有顶点的最短路径值
let P = []; //用于存储图中所有顶点到所有顶点的最短路径序列
for (let i=0;i<G.vexs.length;i++){ //初始化矩阵D和P
D[i] = new Array(G.vexs.length);
P[i] = new Array(G.vexs.length);
for (let j=0;j<G.vexs.length;j++){
D[i][j] = G.arcs[i][j]; //D矩阵与图的邻接矩阵相同
P[i][j] = j; //P矩阵每列的值相同
}
}
for (let k=0;k<G.vexs.length;k++){
for (let v=0;v<G.vexs.length;v++){
for (let w=0;w<G.vexs.length;w++){
if (D[v][w] > D[v][k] + D[k][w]){
//如果经过下标为k顶点路径比原两点间路径更短
D[v][w] = D[v][k] + D[k][w]; //替换权值
P[v][w] = P[v][k]; //路径设置为经过下标为k的顶点
}
}
}
}
console.log(D);
console.log(P);
}
最终D和P矩阵结果如下,D矩阵中存储着图中所有顶点到所有顶点的最短路径值,而矩阵P的存储着各顶点的最短路径序列,例如要查询顶点v0到顶点v8的路径序列,P[0][8]=1, P[1][8]=2, P[2][8]=4, P[4][8]=3, P[3][8]=6, P[6][8]=7, P[7][8]=8,于是序列为0-1-2-4-3-6-7-8
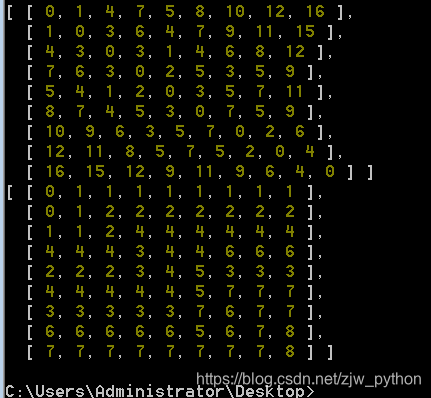
从循环嵌套来看,该算法的时间复杂度为O(n3)
