最短路径
最短路径问题是图的一个经典问题,常用的求最短路径的方法有
(迪杰斯特拉)Dijkstra算法,(弗洛伊德)Floyd算法。
Dijkstra算法用于求单源点最短路径问题,复杂度为O(n2),而Floyd算法用于求对每一对顶点之间的最短路问题(采用枚举法,枚举所有可能),复杂度为O(n3)。
一、Dijkstra算法:
迪杰斯特拉提出了一个按路径长度递增的次序产生最短路的算法,其基本思想是:设置一个集合S存放已经找到最短路径的顶点,S的初始状态只包含源点v,对vi属于V-S,假设从源点v到vi的有向边为最短路径,以后每求得每一条最短路径v,…vk,就将vk加入到集合S中,并将路径v,…vk,vi与原来的假设相比较,取路径长度较小者为当前最短路径。
核心代码如下:
for(int i=1; i<=n-1; i++) //更新dis数组
{
min1=inf;
for(int j=1; j<=n; j++)
{
if(book[j]==0&&dis[j]<min1)//每次找最短的边
{
min1=dis[j];
u=j;
}
}
book[u]=1;
for(int v=1; v<=n; v++)
{
if(e[u][v]<inf)
if(dis[v]>dis[u]+e[u][v])//如果从起始点到j的距离大于起始点到u的距离加上u到j的距离就更新,专业术语松弛操作
dis[v]=dis[u]+e[u][v];
}
}
Dijkstra算法是应用贪心的一个典例。但是也正是因为其贪心算法的思想,其不适用于带负权边的图,例:
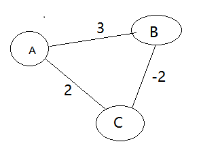
我们利用Dijkstra算法试验一下上面的图(从A->B):
1.先把A点标记,不需要访问本身
2.首先找到距A最近的且直接相连的点(也就是两点间没有中转点)C,把C标记
3.找出C点的出点A,,B,A被标记了不管,此时A到B的距离为3,大于A到C的距离加上C到B的距离0,所以更新A到B的距离为0
4.更新后A到C的距离仍然为2,A到B的距离为0,A,C都被标记,只有B未被标记,进行下一步
5.找到距A最近的且未被标记的点B,标记B
6.找出B的出点A,C,然而A,C两点都被标记,不能松弛
7.程序结束,结果为A到C的距离为2而不是1,说明普通dijkstra算法并不能处理带负权边的无向图
Dijkstra算法求最短路的算法是由贪心得来的,也就是说长路径的松弛正确的前提是用来松弛它的短路径是最短的,也就是说在之后是不会变的,这在非负权值的情况下是对的,然而遇到负权值便错了,因为当加入了负权值边后便可能使之前的短边变得更短。
对Dijkstra算法的改进:
Bellman-Ford(BF算法)(适用于带负权值的边):
Bellman-Ford算法同样是求起始点到各个顶点的最短路,但与dijkstra不同的是,dijkstra每次找到最近的点进行松弛操作,而这个bellman则是只要路程更短就松弛。也是因为这样才能用来解决负权值问题。
核心代码:
for(int k=1;k<=n-1;k++)//进行n-1次松弛(最糟糕的情况,因为可能不到n-1次就已经找出来了)
for(int i=1;i<=m;i++)//枚举每一条边
if(dis[v[i]]>dis[u[i]]+w[i])//尝试松弛每一条边
dis[v[i]]=dis[u[i]]+w[i];
SPFA算法(SPFA是一种用队列优化的B-F算法):
1.初始时,只有把起点放入队列中。
2.遍历与起点相连的边,如果可以松弛就更新距离dis[],然后判断如果这个点没有在队列中就入队标记。
3.出队队首,取消标记,循环2-3步,直至队为空。
4.所有能更新的点都更新完毕,dis[]数组中的距离就是,起点到其他点的最短距离。
SPFA如何判断成环:
在储存边时,记录下每个点的入度,每个点入队的时候记录一次,如果入队的次数大于这个点的入度,说明从某一条路进入了两次,即该点处成环。
二、Floyd算法:
Floyd算法用于求每一对顶点之间的最短路径问题,给定带权有向图G=(V,E),对任意顶点vi和vj(i!=j),求顶点vi到vj之间的最短路径。
解决这个问题的方法(借助Dijkstra算法)是:每次以一个顶点为源点,调用Dijkstra算法n次,便可得到每一对顶点之间的最短路径,时间复杂度为O(n3)。
Floyd算法:
一般来说我们从i到j有两种走法:
1.直接从i到j
2.通过中间点k中转,i->k->j
所以我们就遍历所有情况,如果通过某个中转点距离小于直接到达的距离,就更新这两点间的距离。(Floyd算法)
核心代码如下:
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
{
if(map1[i][j]>map1[i][k]+map1[k][j])
map1[i][j]=map1[i][k]+map1[k][j];
}
因此Floyd算法能解决负边(负权)但不能解决负环。
上述几种求最短路径的方法仅限于求不带环的图中:
1.Dijkstra算法不能解决带负权边的图
2.B-F算法做了优化允许图中出现负权边并解决该问题
3.SPFA算法利用队列对B-F算法进一步优化,允许图中可以出现环但是不能解决带环的图(仅能判别出现但是不能解决)
4.Floyd算法能解决负权边但不能解决负环
我们可以假设某一条环上路径长度为负(单循环时),那么我们就可以进行多循环直至无限循环无限缩短路径长度,那么问题便无解了。因此任何算法都不能求带环的问题。